Лекции / Лекции (МП-3 Земсков) / Лекции (word) / Лекци22

Лекция 22.

 6.5.3. Проверка гипотез о сравнении характеристик в двух независимых генеральных.

 6.5.3.1. Распределение Фишера.

Теорема Фишера. Пусть V₁~ V₂~ причем V₁ и V₂ независимы. 

 ~ без доказательства.

похоже на - распределение.

 6.5.3.2. Сравнение дисперсией.

Подстановка задачи. Пусть Х~, Y~ причем X и Y – независимы (все

параметры неизвестны)

( в статическом смысле)

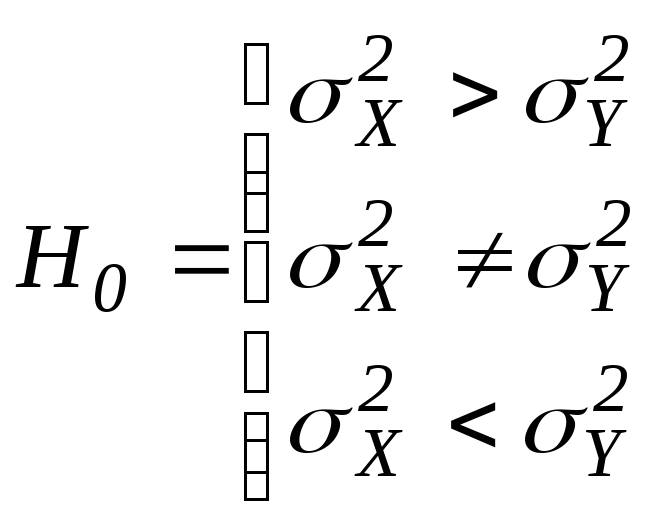
 задоно.

Имеются выборки: , .

Теорема 22.1. При условиях, наложенных на генеральные совокупности статика:

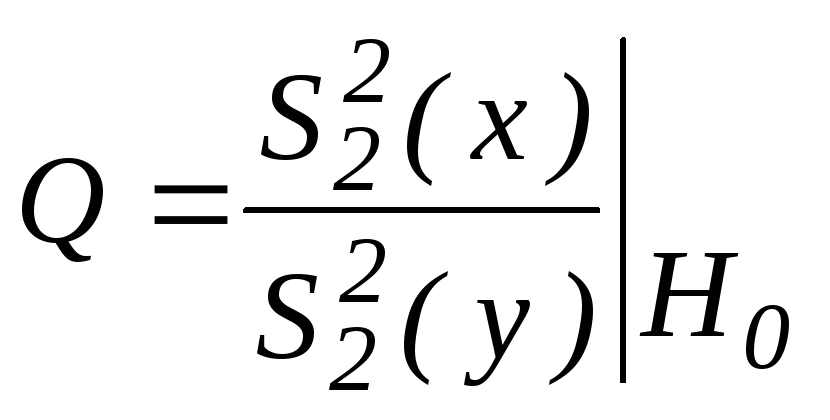~ (1)

параметры в порядке деления чисел на знаменатель.

~

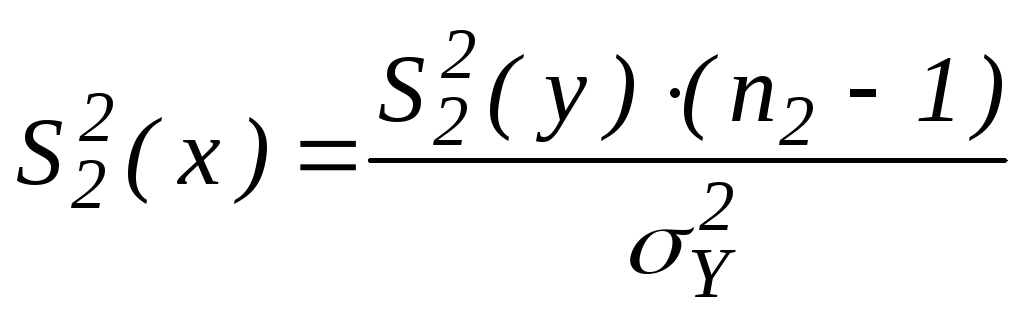Ясно, что и независимы.  по теореме Фишера имеем:

~.

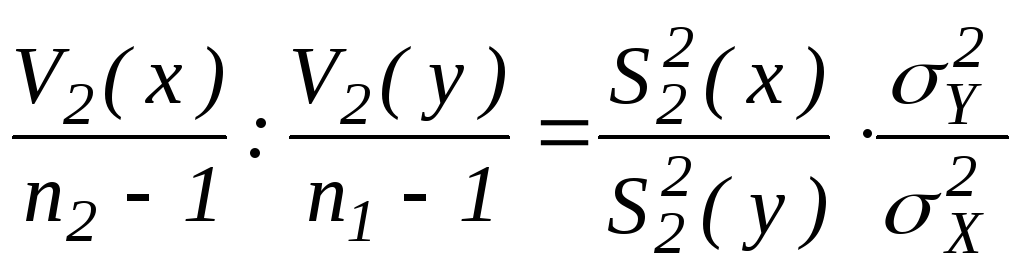При условии Н­₀ дисперсии в выражении для Q сокращаются.  Теорема доказана.

В таблице F­­­_i распределения приводятся значения для значений > 1.

При проверке левосторонних гипотез, используем (1) получим значения <1  нужно менять квантили. Найти квантиль, соответствующую 1- на право хвосте, а затем 1 поделить на полученное число.

найти квантиль, соответствующую 1- на право хвосте, а затем 1 поделить на полученное число 

Q<1

Замечение 1. Если в постановке решаемой задачи математические ожидания m_X и m­_Y иизвестны, то следует использовать статику ~

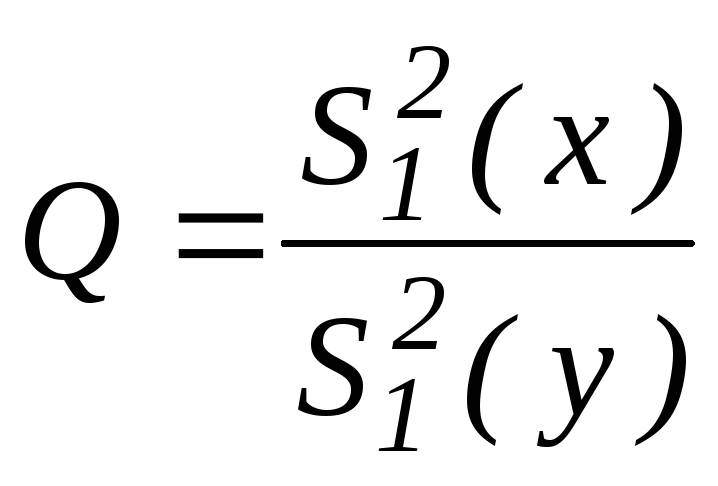 6.5.3.3. Сравнение средних (математических ожиданий).

Постановка задачи та же.

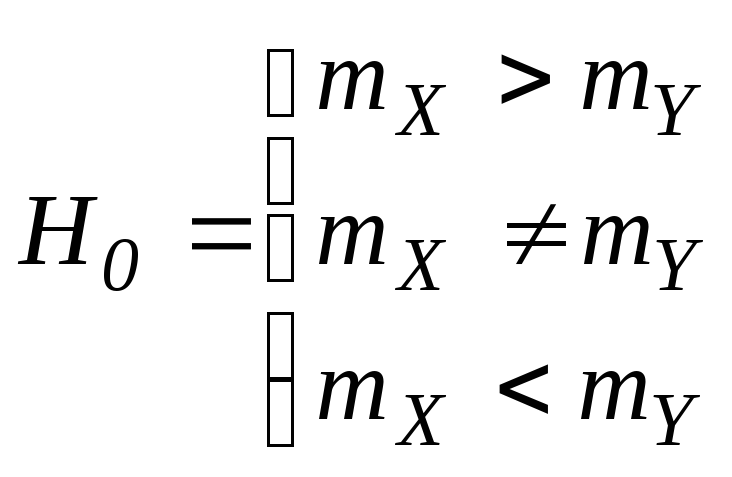
Случай 1. и - известны.

Подходящая статика:

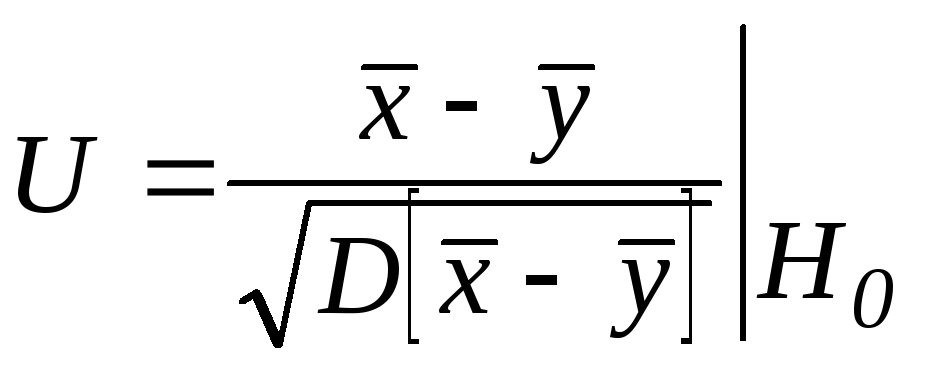~ N(0,1).

U – есть линейная комбинация нормальных величин  композиция устойчива  U ~ N(0,1).

Предположим, что Н­₀ верна. 



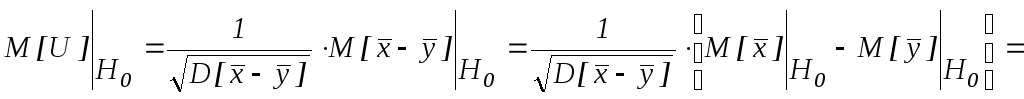
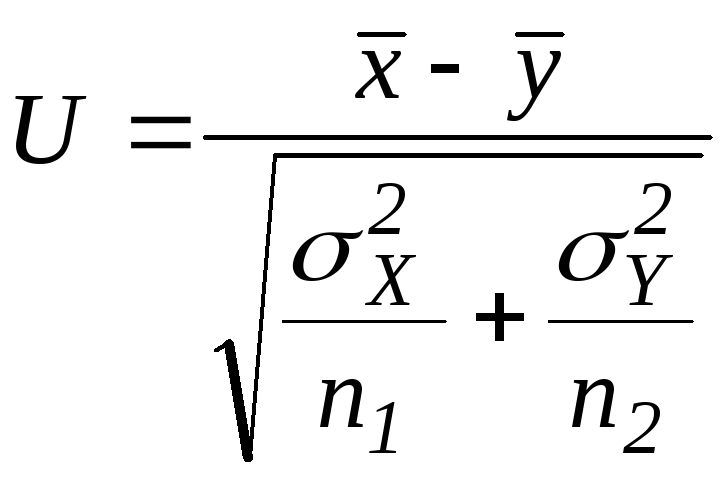~ N(0,1) (1)

Далее по общей методике.

Случай 2. и - неизвестны.

В этом случае U, определенное в (1) использовать нельзя.

Случай 2.1. Дисперсии неизвестны, но подтверждается гипотеза об их равенстве.

- подтверждается на уровне  .

Случай 2.2. Гипотеза отклоняется.

Рассмотрим случай 2.1.

- запишем так:

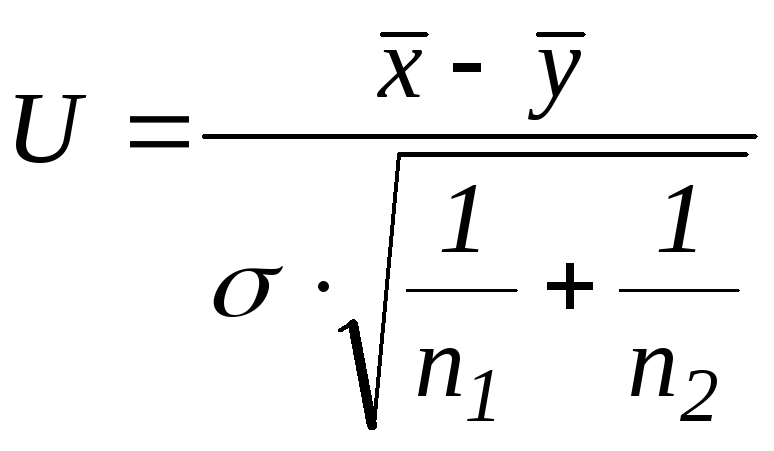~ N(0,1), но - мешающий параметр.

Теорема 22.2. Обозначим (2)

несмещенная выборочная дисперсия объединенной выборки.

- оценка неизвестна. .

Составим статику ~

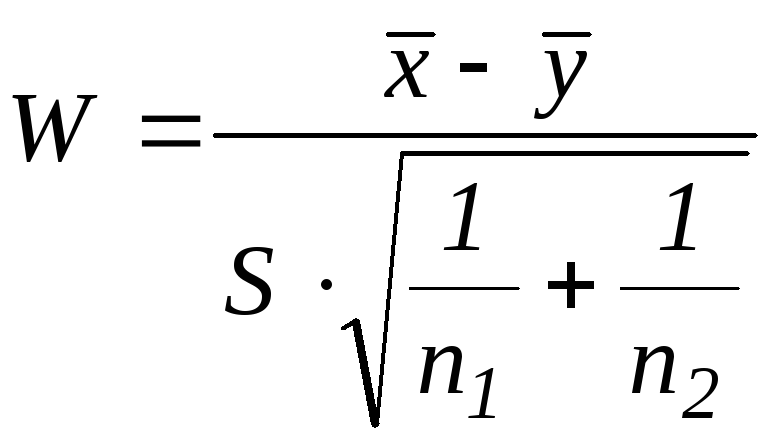преобразуем (2):

+ +

=

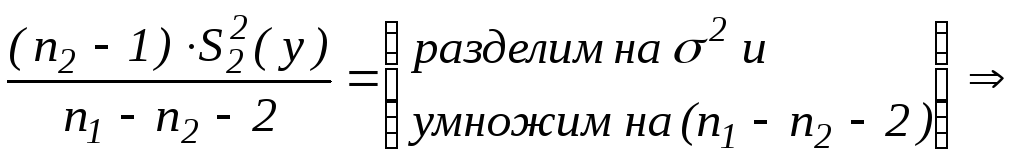
Очевидно, что ~

~

- распределение с композиционно устойчиво ~

Преобразуем:

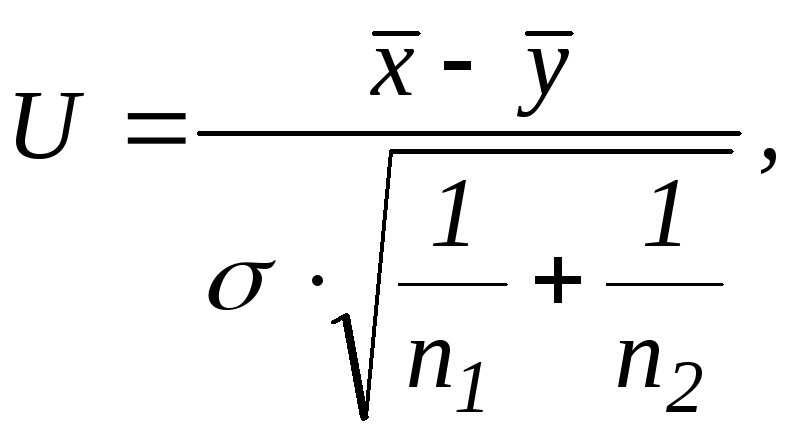
где  по теореме Пирсона ~

Рассмотрим случай 2.2.

не выполняется  статистика W – неприменима  используется так называемая статистика Уэлчи:

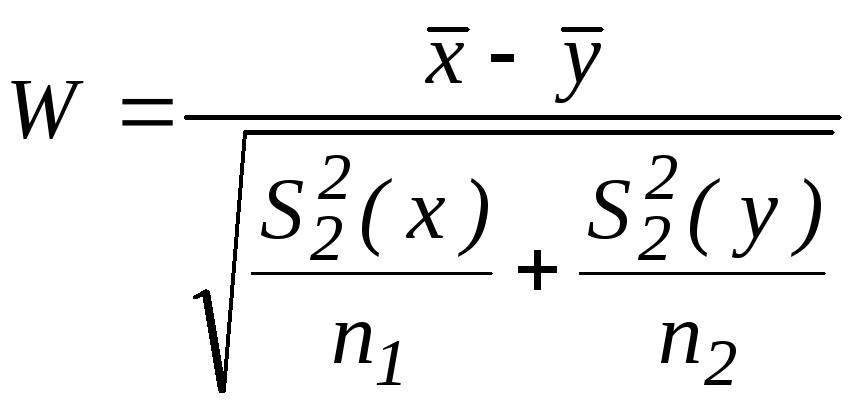~, где

.

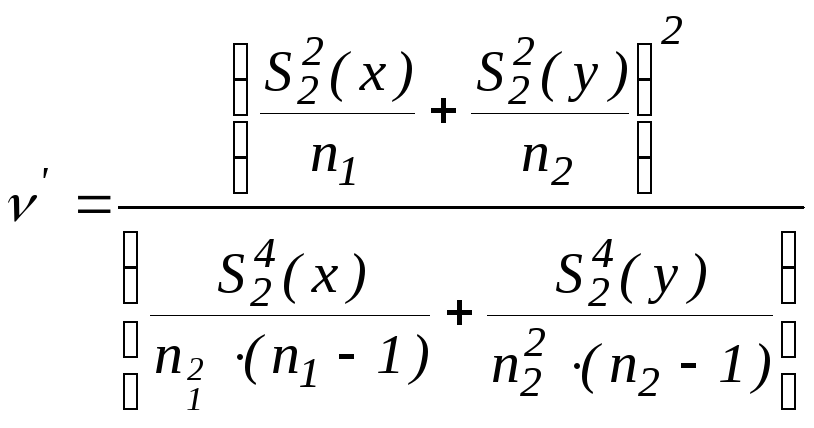
 6.5.3.4. Сравнение вероятностей.

X~B(1,P₁) – индикатор;

Y~B(1,P₂) – индикатор.

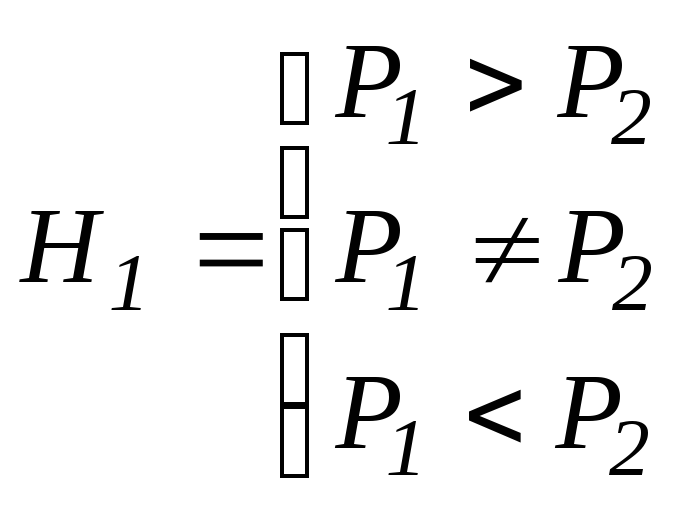Имеем выборки из X и Y:

- относительная частота;

- относительная частота.

Подходящая статика:

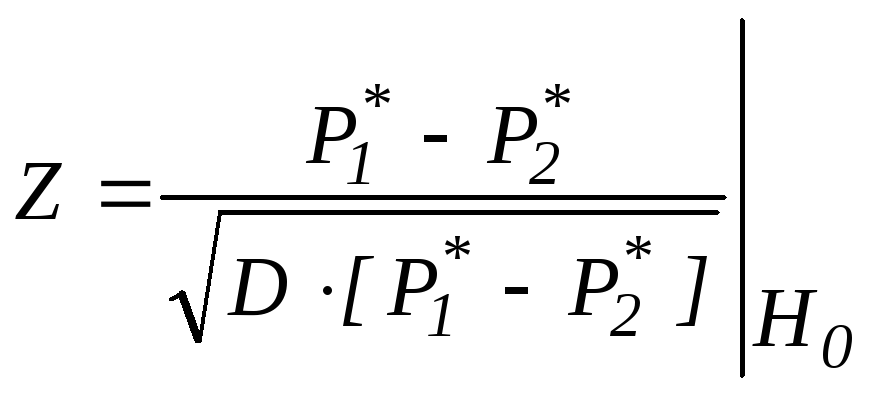~ N(0,1) при n>>1 (по теореме Лапласа-Муавра).

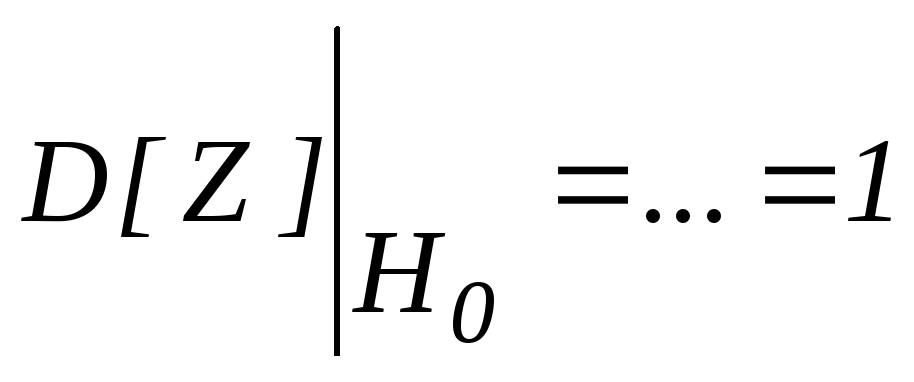
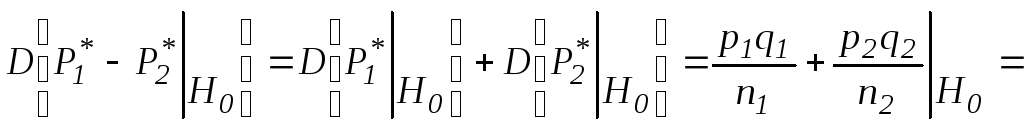
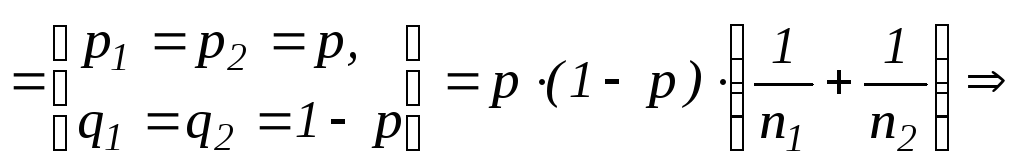
Статика: 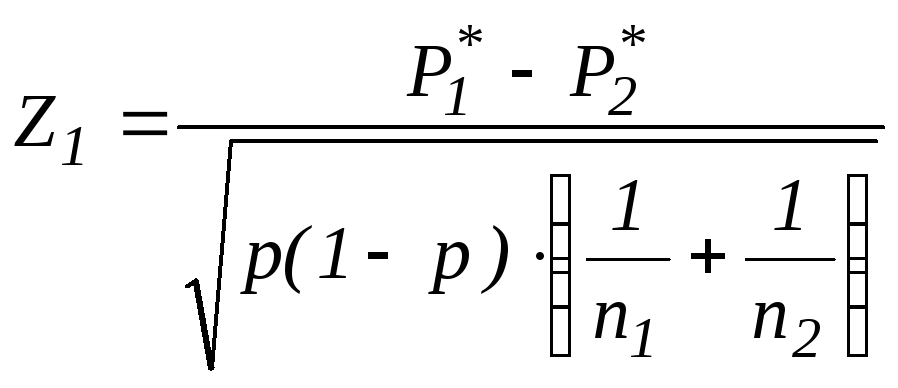~N(0,1) при

При условии:

Неизвестное р оценивается по объединенной выборке.

Было: ; (4)

Статика Z приобретает вид, где .