
Лекции / Лекции (МП-3 Земсков) / Лекции (word) / Лекци24
.docЛекция 24.
6.7. Корреляционный анализ.
Коэффициент корреляции является индикатором линейной зависимости.
Из теории вероятности:
![]() - нормированная
корреляция или коэффициент корреляции.
- нормированная
корреляция или коэффициент корреляции.
Существует выборка
из двумерного распределения (X,Y):
![]()
![]() -
выборочный коэффициент корреляции.
-
выборочный коэффициент корреляции.
Обозначим:
![]() ,
,
![]() ,
,
![]() -
выборочная дисперсия по x.
-
выборочная дисперсия по x.
![]() -
выборочная дисперсия по y.
-
выборочная дисперсия по y.
![]() -
выборочный коэффициент корреляции.
-
выборочный коэффициент корреляции.
Проверка гипотез о корреляции.
-
о наличии корреляции
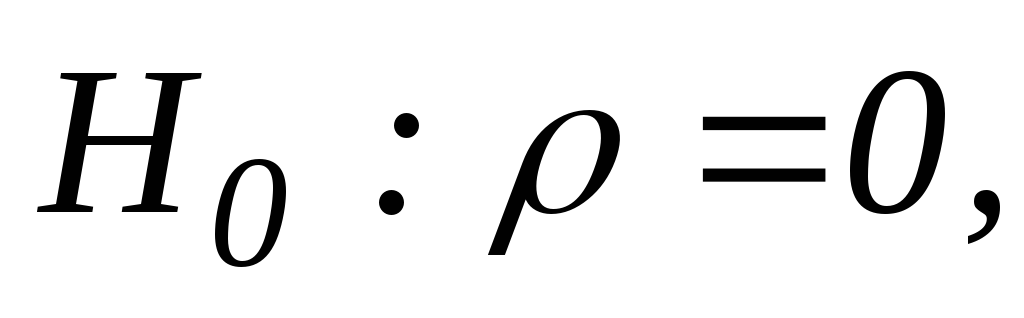
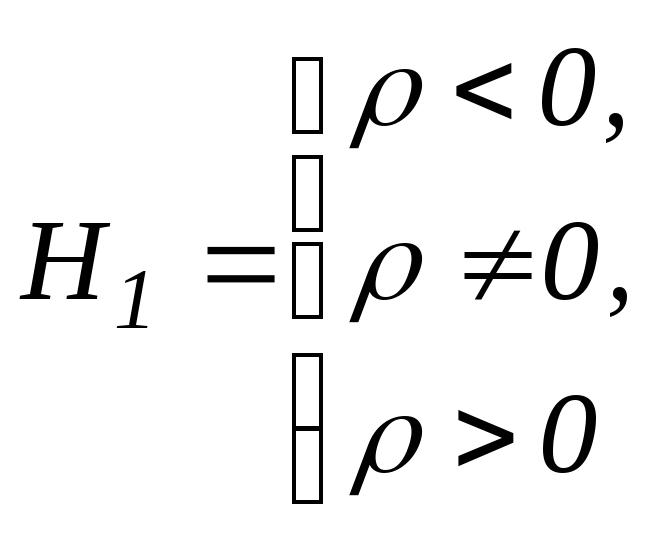
-
сравнение с эталоном
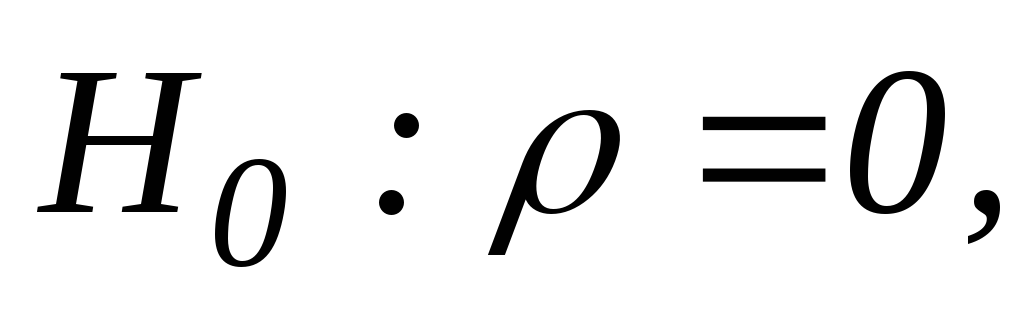
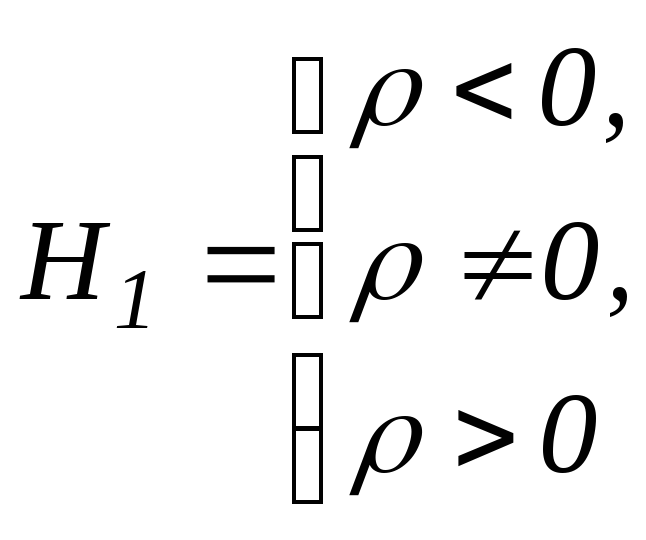
Для случая (1) используется статистика St
![]() ~St(n-2)
(1)
~St(n-2)
(1)
Для случая (2) и (1)
(если
![]() )
используется статика Фишера:
)
используется статика Фишера:
![]() ,
где
,
где
![]() - преобразование Фишера;
- преобразование Фишера;
Н быстрее N(0,1) , чем r.
![]()
![]()
При этом Z~N(0,1), быстрее, чем в первом случае.
Пример 1.
x |
8 |
10 |
5 |
8 |
9 |
|
y |
1 |
3 |
1 |
2 |
3 |
Вычислить rxy и проверить гипотезу о его наличии.
![]()
![]() ;
;
![]() ;
;
 ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]()
![]() ;
;
![]() ;
;
Проверим гипотезу (1):
![]()

Используем Стьюдентову статистику:
![]()
![]() .
.
Если считать по Фишеру (2), то:
![]()
H0
будет
принята;
H0
будет
принята;
![]()
H1
отвергается.
H1
отвергается.![]()
Пример 2.
Совершена повторная выборка (смотри пример 1), n=28 r=0,51; =0,05. C помощью статистики Фишера (2):
![]() ;
;
![]() H0
–
отвергается.
H0
–
отвергается.
§ 6.8. Регрессивный анализ.
В теории вероятности:
![]() - некоторая
функция от Х,
уравнения регрессии.
- некоторая
функция от Х,
уравнения регрессии.
Хреновая диаграмма
Диаграмма рассеивания.
Строим кривую, которая наилучшим образом проходит через облако точек.
Строим модель
регрессии:![]() ,
,
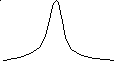
где к
- шум модели ( ),
так как 2
не зависит от номера измерения, то
говорят, что измерения равноточное.
),
так как 2
не зависит от номера измерения, то
говорят, что измерения равноточное.
Неизвестное: а
– вектор,
![]() ,
а сама функция – известна.
,
а сама функция – известна.
Вектор а отыскивается методом наименьших квадратов:
![]() ;
;
так как лучше всего согласуется с принципом максимального правдоподобия.
Теорема.
Критерий (3) соответствует признаку максимального правдоподобия.
![]()
![]() ,
,
а измерения
выполняются независимо
![]() -
независимы в совокупности.
-
независимы в совокупности.
Составим функции
правдоподобия для вектора
![]() :
:
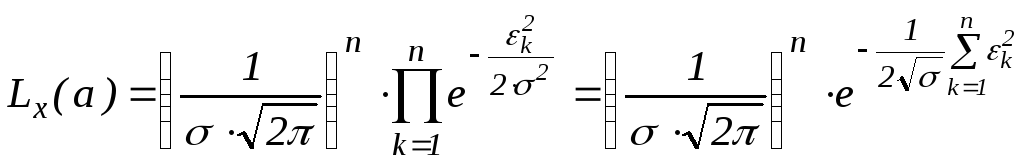
maxLx(a)
maxLx(a)![]()
![]() .
.![]()
Пример.
![]() Построение прямой
регрессии (зависимость между x
и
y
пытаются
приблизитьсяк
прямой).
Построение прямой
регрессии (зависимость между x
и
y
пытаются
приблизитьсяк
прямой).
![]() ,
Х –
контролируемая
переменная
может быть вычислена с любой точностью
и в любой точке.
,
Х –
контролируемая
переменная
может быть вычислена с любой точностью
и в любой точке.
Точки
![]() - план эксперимента. Пусть эти точки
заданы. Рассмотрим модель:
- план эксперимента. Пусть эти точки
заданы. Рассмотрим модель:
![]() .
.
Оценим a и b по методу наименьших квадратов:
![]() ;
;
![]() включает ошибку
изменения yk
и ошибку вычислений, и так далее.
включает ошибку
изменения yk
и ошибку вычислений, и так далее.
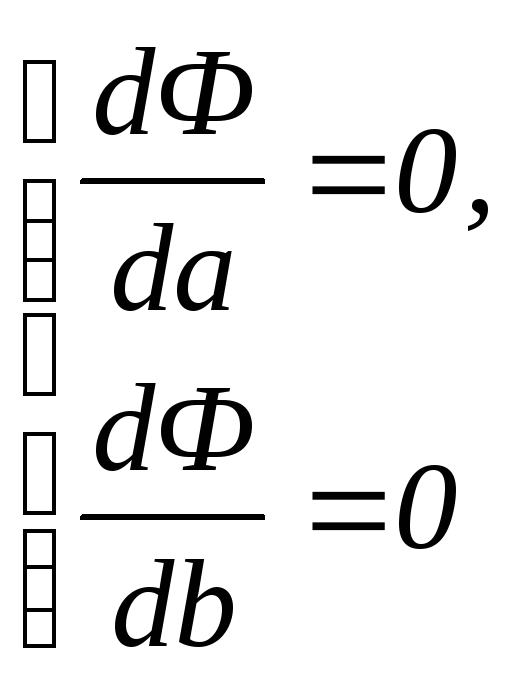
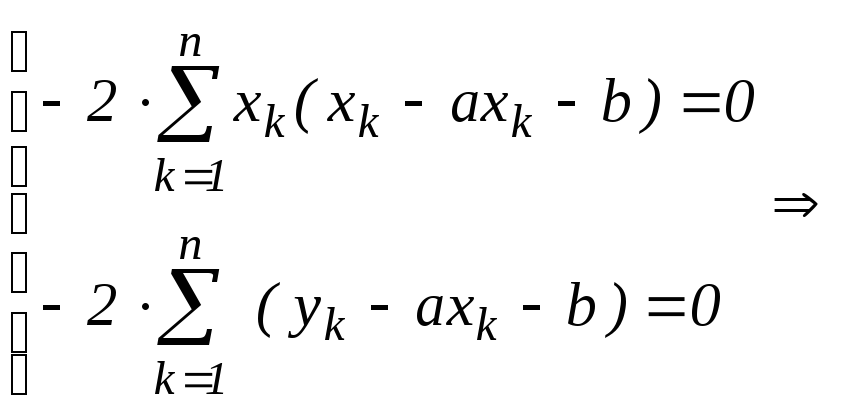
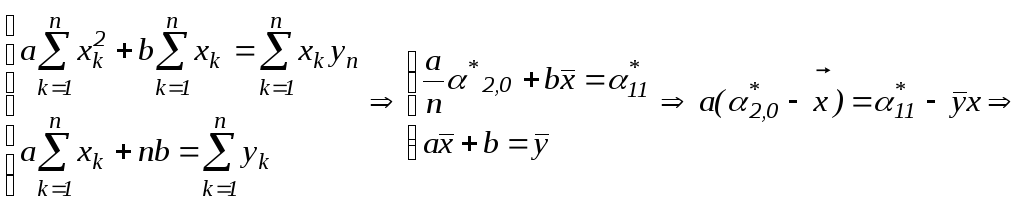
![]()
![]()
![]()
![]()
![]() - проходит
через центр рассеивания
- проходит
через центр рассеивания
![]()
![]() - ответ.
- ответ.
![]()
Как проверить адекватность модели?
Задача. Проверить гипотезу об адекватности модели регрессии.
В каждом измерении y содержится ошибка измерения.
Эта задача решается методом дисперсионного анализа.
6.9. Дисперсионный анализ.
Задача дисперсионного анализа.
Имеется l
независимых
генеральных совокупностей
![]() ,
причем известно, что
,
причем известно, что
![]() ~
~![]() .
.
![]()
![]()
Делается выборка:
Массив
![]() i=1,2,….l,
j=1,2,….ni
–номер
измерений.
i=1,2,….l,
j=1,2,….ni
–номер
измерений.
![]() -
из Х1;
-
из Х1;
![]() из Х2;
из Х2;
……………………….
Методология Фримера: берутся две специальные дисперсии, для этого:
-
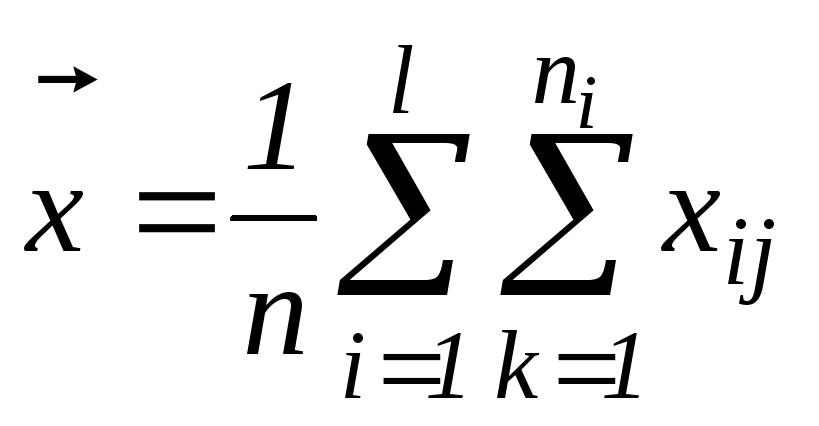 ,
,
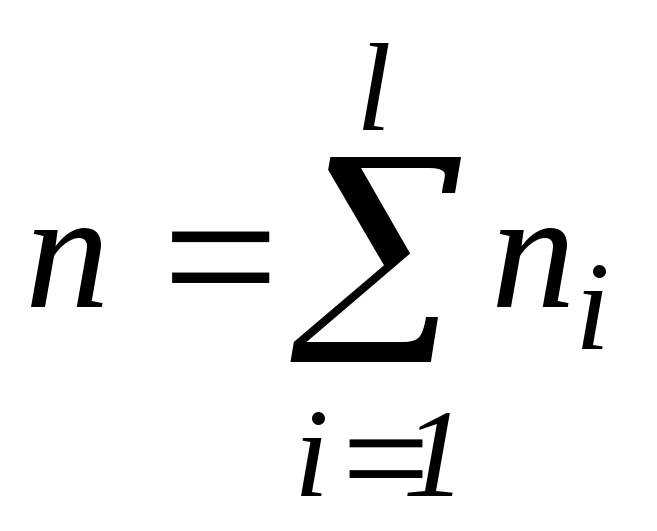 ,
,
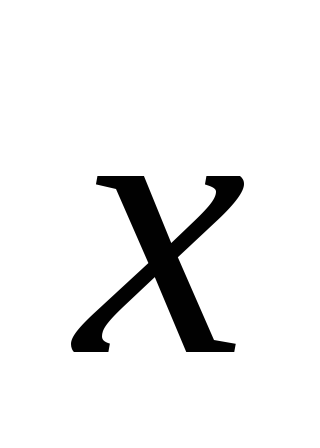 - тотальное (глобальное) среднее для
всего массива.
- тотальное (глобальное) среднее для
всего массива. -
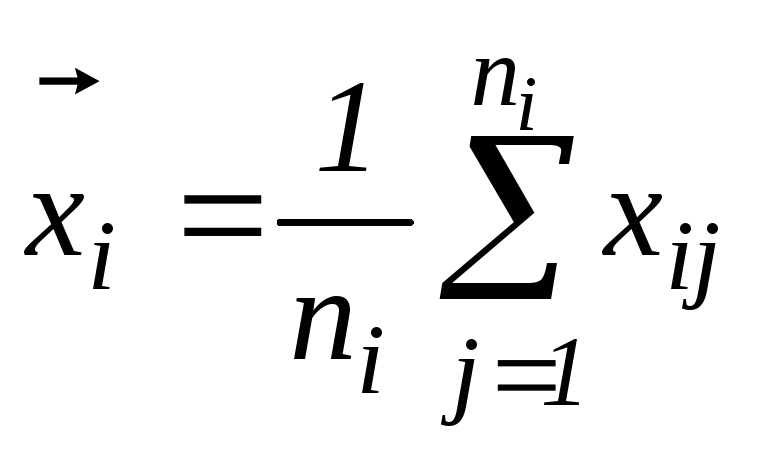 ,
,
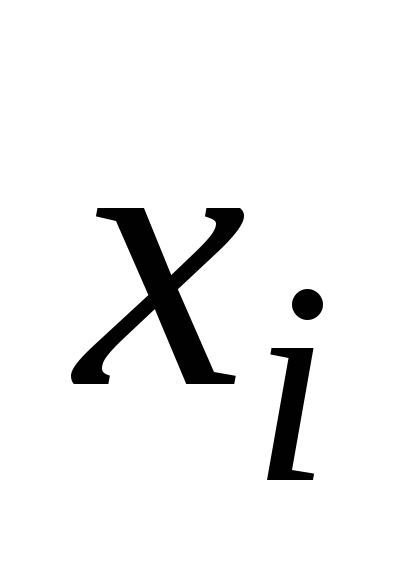 -
внутригрупповое среднее.
-
внутригрупповое среднее. -
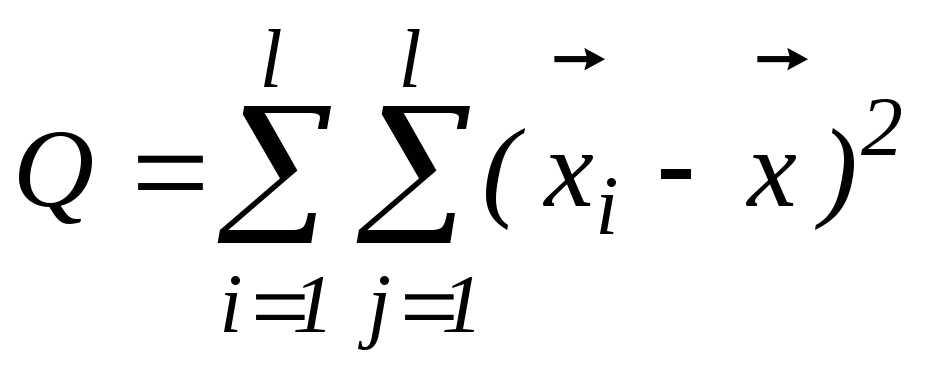 -
полная сумма квадратов.
-
полная сумма квадратов. -
Q разбивается на две суммы:
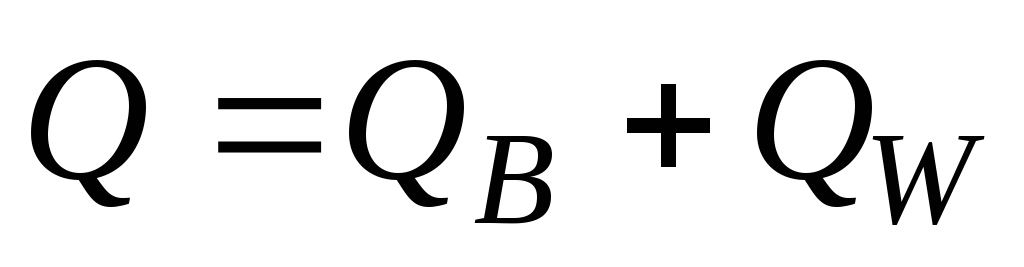
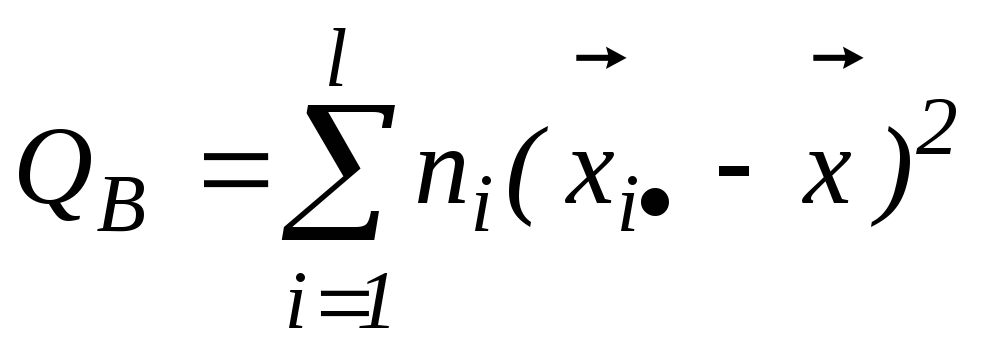 -
межгрупповая сумма;
-
межгрупповая сумма;
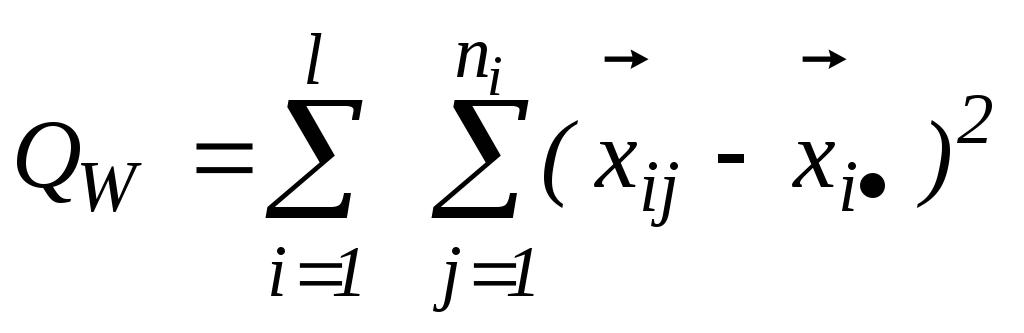 -
внутригрупповая сумма
-
внутригрупповая сумма
![]() ,
где
,
где
![]() -
число степеней свободы.
-
число степеней свободы.
![]() -
используется композиционная устойчивость
распределения Фримера.
-
используется композиционная устойчивость
распределения Фримера.
![]()
-
Для проверки гипотезы Н0 составляем статистику:
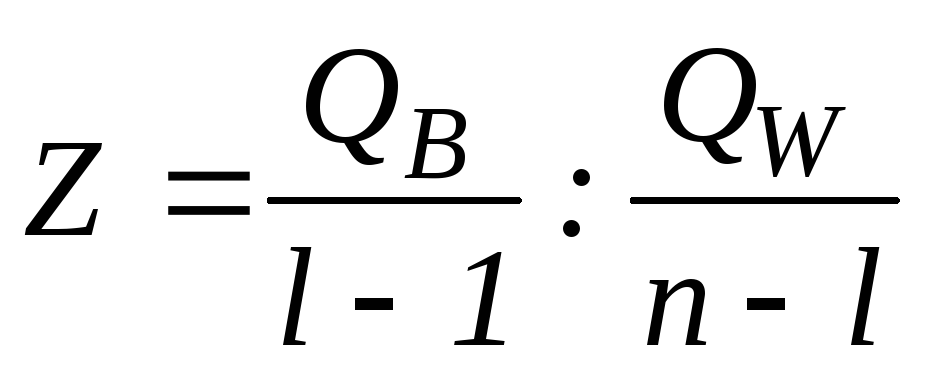 ~
~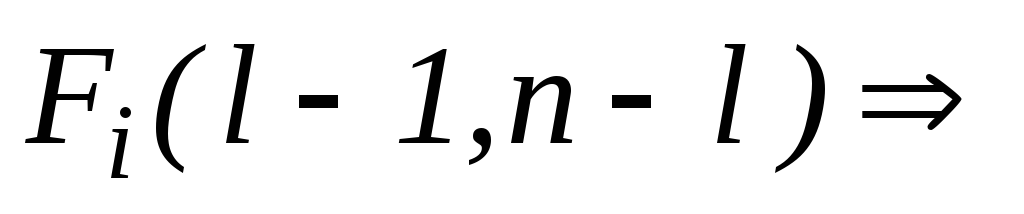
далее гипотеза проверяется по стандартному алгоритму.
Проверка адекватности модели регрессии (на примере прямой линии).
Нельзя проверить адекватность только одного измерения, т.к. тогда нет информации об ошибках.
![]() ,
где
,
где
![]() -
строится по средним точкам.
-
строится по средним точкам.
![]() -
сумма «между»
-
сумма «между»
![]() .
.
![]() -
сумма «внутри»
ошибка.
-
сумма «внутри»
ошибка.
![]()
![]()
Составляем статику:
![]() ~
~![]()
Если Н0 – отвергается, то модель неадекватна полиномиальная аппроксимация (кривая на порядок выше) плюс проверка аддитивности и т.п. пока Н-0 не примется.
