Лекции / Лекции (МП-3 Земсков) / Лекции (word) / Лекци5
.doc
2) Полиномиальная схема
k={1, 2,…,N}, k=1..N
n-число проведенных опытов
Событие Вn,m1,m2,m3,…,mN=
{в n опытах исход 1 осуществился m1 раз,
в n опытах исход 1 осуществился m1 раз,
в n опытах исход 2 осуществился m2 раза,
----------------------------------------------------
в n опытах исход N осуществился mN раз}
Это событие состоит
из слов: символ 1
встречается m1
раз, 2
— m2 раза, и т.д. Каждое такое слово
независимо от расстановки символов
имеет вероятность
![]() ,
при этом выполнены условия:
,
при этом выполнены условия:
1) m1+m2+…+mN=N
2) P(k)=Pk => P1+P2+…+PN=1
Таких слов всего (по схеме упорядоченных событий):
![]() ,
где m1!m2!…
mN!
- число упорядоченных разбиений (равно
числу слов)
,
где m1!m2!…
mN!
- число упорядоченных разбиений (равно
числу слов)
Тогда общая
вероятность P(Bn;
m1; m2; …
mN )=
![]()
![]()
Пример 4.5 Два равносильных шахматиста играют матч из 12 партий (результат последующей не зависит от результата предыдущей. Множество исходов k={1-й выиграл, 2-й выиграл, ничья} Вероятность того, что выиграет первый шахматист равна 0,2 ; второй —0,2; вероятность ничьи —0,6. Найдем вероятности А={1-й выиграл 3 партии, 3 — проиграл, остальные — ничья}, В={1-й выиграл матч, т.е. выиграл 6 партий}
Решение:
АВ12;3,3,6
=> P(A)=![]() 0,0055
0,0055
Можно упростить решение, использовав равносилие: либо один выиграл, либо ничья. P(B)-P(ничья в матче)=1
Р(ничья в матче)=Р(0,0,12)+Р(1,1,10)+…+Р(6,6,0)
Глава 2. Случайные величины
§1.1 Основные понятия, связанные со случайной величиной.
Пусть опыт полностью формализован, т.е. Э{, F,P}. Рассмотрим какую-либо функцию X(), , отображающую в R ( =>R). При некоторых дополнительных условиях X() называется случайной величиной, т.к. можно лишь с вероятностью сказать, какое значение примет X().
Пример 5.1 3 Раза подбрасывается монета. Определим случайную величину Х — число выпавших гербов. Построить явно эту функцию.
Решение:
={111, 011, 101,110,100,010,001,000}
Всего исходов 23=8, x 3,2,2,2,1,1,1,0
Определение: Ех={0,1,2,3} — множество возможных значений случайной величины.
Определение: Ех — спектр X()
Пример 5.2 Наудачу выбирается точка в единичном квадрате. Определть Z — расстояние от точки до начала координат. Выразить явно Z через исходы.
Решение.
= {(x,y)}|
0![]() x
x![]() 1,
0
1,
0![]() y
y![]() 1}
1}
Z()=![]()
Ez=[
0,![]() ]
— возможный
спектр Z()
]
— возможный
спектр Z()
Ez—случайная величина непрерывного типа (в примере 5.1 Ez —случайная величина дискретного типа)
Определение: Случайной величиной называется числовая функция X() такая, что для любого х из ножества действительных чисел R (x R ) множество тех , для которых выполняется условие X()<x принадлежит алгебре событий F для данного опыта. (Краткая запись: { | X()<x , x R} F ). В дальнейшем будем писать сокращенно : {X<x}
Случайные величины связаны с неравенствами. Все неравенства измеримы.
Действительно,
по определению алгебры {X![]() x}=
x}=![]()
Событие
{x1![]() X
X![]() x2}={X
x2}={X![]() x1}{X<x2}
F, т.е.
может быть рассмотрено, как произведение.
x1}{X<x2}
F, т.е.
может быть рассмотрено, как произведение.
Рассматриваемая в примере 5.1 функция X() является случайной, т.к. —конечно, следовательно множество всех подмножеств из конечного множества также конечны, поэтому совокупность подмножеств автоматически образует алгебру.
Рассматриваемая в примере 5.2 функция Z() будет случайной, если в качестве алгебры событий F будет рассматриваться совокупность всех квадрируемых (по Лебегу) подмножеств из .
§2.2 Функция распределения случайно величины и ее свойства.
Определение: Функцией распределения случайной величины X называется действительная функция действительного переменного, определяемая следующим равенством:
Fx(x)=P{X<x} (1)
Свойства Fx(x):
-
Fx(x) определена для любого х R, причем 0
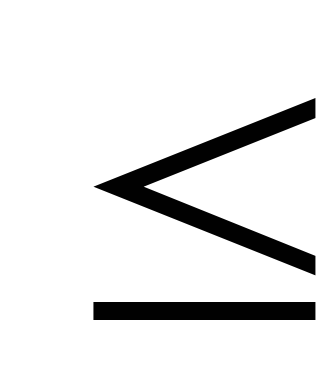 Fx(x)
Fx(x)
 1
1 -
Fx(-
 )=0,
Fx(+
)=0,
Fx(+ )=1,
т.к.
события {X<-
)=1,
т.к.
события {X<- )=,
{X<+
)=,
{X<+ )=
)=
-
Fx(x) — неубывающая функция переменной х.
(Действительно, пусть х1<x2 => {X<x1}{X<x2}=>(по следствию из аксиом)
Fx(x1)![]() Fx(x2)
Fx(x2)
-
Fx(x) — непрерывна слева для всех х R
-
Вероятность попадания на полуинтервал P{x1
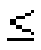 X
X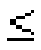 x2}=
Fx(x2)
- Fx(x1)
(2)
x2}=
Fx(x2)
- Fx(x1)
(2)
Доказательство:
Ясно,
что {X<x2}={X<x1}+{x1![]() X
X![]() x2}
P{x1
x2}
P{x1![]() X
X![]() x2}=
Fx(x2)
- Fx(x1)
x2}=
Fx(x2)
- Fx(x1)
Эти свойства универсальны, т.е. не зависят от ого дискретна или непрерывна функция X().
Определение: Случайная величина называется случайной величиной дискретного типа (СВДТ), если множество ее значений конечно, счетно и прерывно.
Определение: Случайная величина называется случайной величиной непрерывного типа, если множество ее значений образует интервал на действительной оси.
§2.3 Закон распределения случайной величины дискретного типа.
Определение: Законом распределения СВДТ называется таблица, состоящая из двух строк: в первой строке перечисляются все возможные значения случайной величины, а во второй строке указываются соответствующие вероятности их реализаций. При этом должно выполняться обязательное условие нормировки:
![]() ,
хk
Ех
,
хk
Ех
Пример 5.3 Описать закон распределения случайной величины Х из примера 5.1
Решение:
-
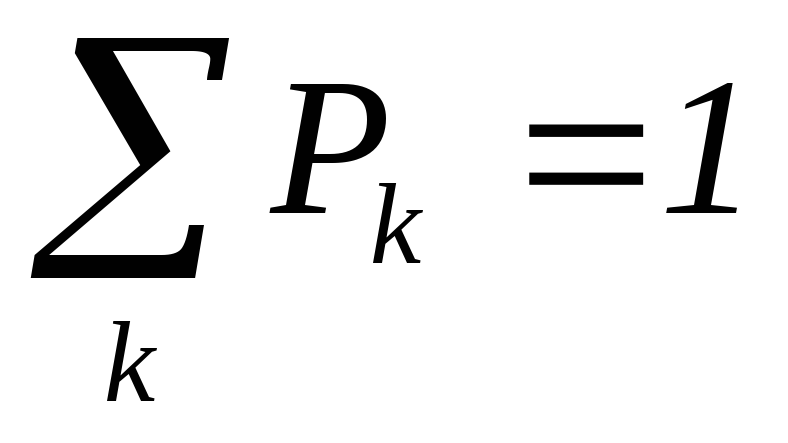
Х
0
1
2
3
P
1/8
3/8
3/8
1/8
P{X=0}=P{(000)}=![]()
P{X=1}=P{(100)}+
P{(010)}+ P{(001)}=![]()
Пример 5.4 Пусть Э — последовательность испытаний по схеме Бернулли. Рассмотрим случайную величину Х - число успехов в n опытах по схеме Бернулли. Описать Закон распределения случайной величины Х.
Решение:
Очевидно, что Ех={0,1,2,…,n}. Ясно, что событие {X=k}=Bn,k по формуле Бернулли
(3) P{X=k}=![]() ,
где Р
— вероятность успеха в одном опыте;
,
где Р
— вероятность успеха в одном опыте;
q=(1-p); k=0,1,…,n
Определение: Распределение, описываемое формулой (3) , называется биномиальным распределением с параметрами n и p
(Кратко: ХB(n,p))
Пример 5.5
Убедиться,
что распределение, полученное в примере
5.3 является биномиальным с параметрами
n=3,
p=![]()
Решение:
Например, P{X=2}=![]() .
С
другой стороны, если ХB(3,
.
С
другой стороны, если ХB(3,![]() )
P{X=2}=
)
P{X=2}=![]() =
=![]() и т.д.
и т.д.
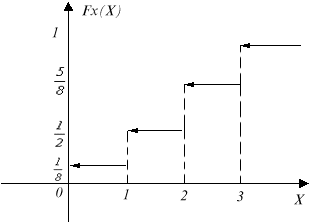
Пример 5.6 Описан закон распределения СВДТ, т.е. задана таблица. Построить функцию распределения Fx(x).
Решение:
Fx(x)=
P{X=x}=![]() (5)
(5)
![]()
(5) говорит от том, что Fx(x) является функцией комплексных вероятностей.
Построим график Fx(x) для примера 5.3