Лекции / Лекции (МП-3 Земсков) / Лекции (word) / Лекци17

Глава 6. Основные понятия математической статистики.

§6.1 Вводные понятия.

В данном разделе рассматриваются методы обработки экспериментальных данных с целю получения объективных выводов о свойствах измеряемой случайной величины.

Определение. Генеральной совокупностью (генеральной случайной величиной) называется исследуемая случайная величина. (Х - ГСВ)

Определение. Выборка из генеральной совокупности объема n - это n измеренных значений случайной величины Х записанных в порядке поступления этих измерений (обозначается: x₁, x₂, x₃,…, x_n).

Определение. Выборка апостериори - выборка после того, как она получена; ряд конкретных чисел x₁, x₂,…

Определение. Выборка априори - n случайных величин, одинаково распределенных и независимых в совокупности.

Определение. Выборочный вектор (X₁,…,X_n) - это n-мерный вектор, у которого все компоненты одинаково распределены и независимы.

Задачи математической статистики:

1. предварительная обработка;

2. задача оценивания;

- точное оценивание;

- интервальное оценивание;

3. корреляционный анализ - исследование стохастической зависимости между случайными величинами;

4. проверка статистических гипотез;

§6.2 Первичная обработка выборки.

Пусть Х~B(10,p), p - неизвестный параметр. Выборка из этого измерения: x₁, x₂, x₃,…, x_n, где x_i {0,1,2,…10}. Целью исследования будет оценка параметра р. Если Х - СВНТ (например, X~N(m,), m,  - неизвестны), то выборка x_i R. Весь вопрос в точности измерений. Если точности недостаточно, то могут быть повторы.

Типы выборок.

1. Простая выборка - числа записаны в порядке поступления (x₁, x₂, x₃,…, x_n)_.

2. Частотная выборка (для дискретного распределения)

x	x1	x2	…	xl
p*			…

где n_i - число измерений, равных x_i.

3) Интервальная выборка. (Х-СВНТ)

Объем такой выборки очень велик, поэтому использовать в простом виде невозможно. Задается число интервалов l:

x₁, x₂, x₃,…, x_n преобразуется в вариационный ряд x⁽¹⁾ x⁽²⁾ … x⁽ⁿ⁾.

x⁽ⁿ⁾- x⁽¹⁾ называется размахом, - шаг.

Получаем таблицу:

№ интервала	1	2	…	l
интервал	(a0,a1]	(a1,a2]	…	(al-1,al]
число выборок, попавших в интервал	n1	n2	…	nl
относительная частота			…

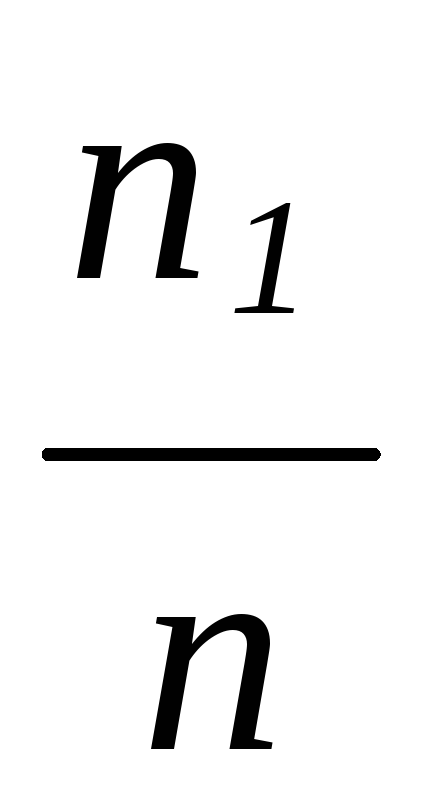
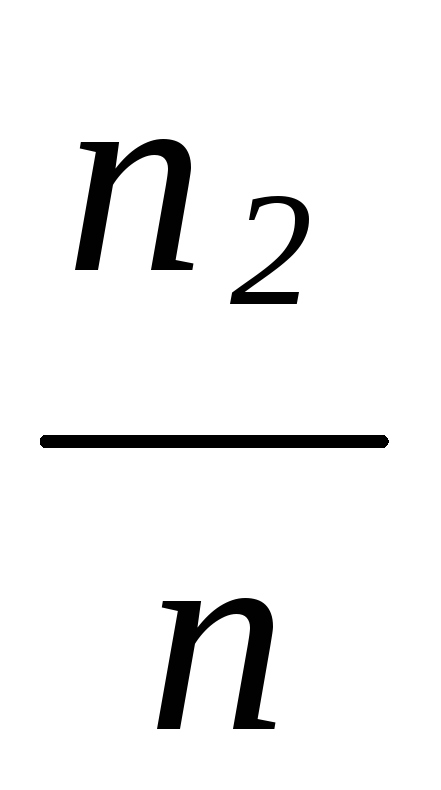
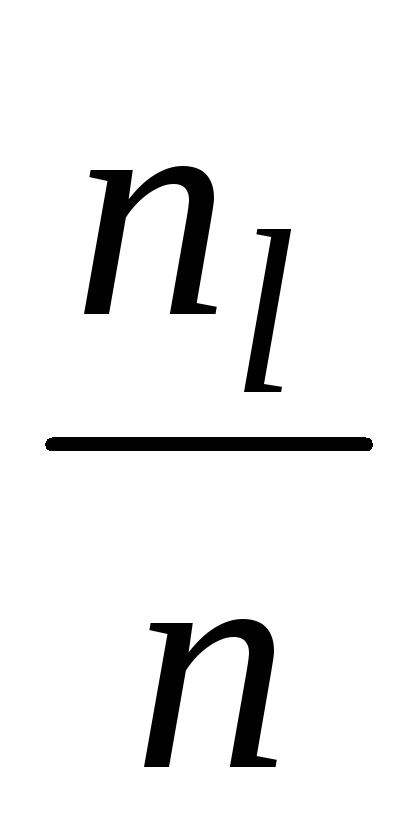
Определение. Выборочное (эмпирическое) распределение - таблица в случае 2) , либо для случай 1) таблица:

x	x1	x2	x3	…	xn
p*				…

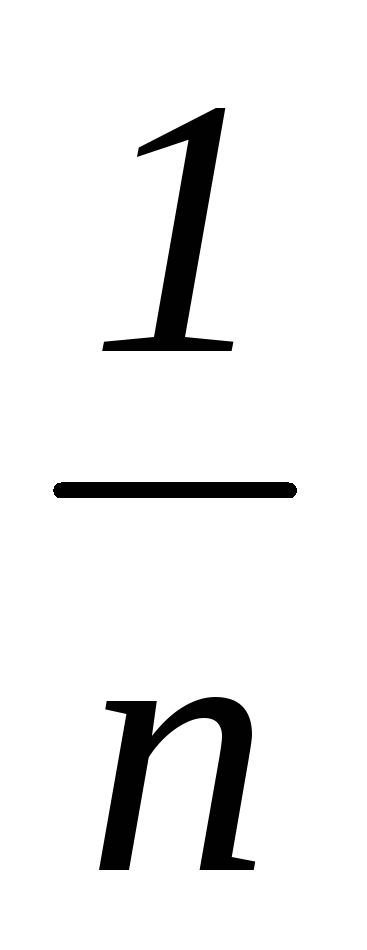
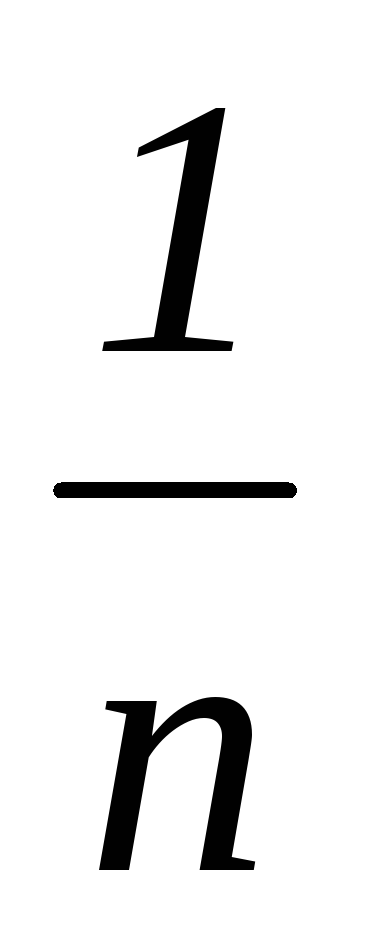
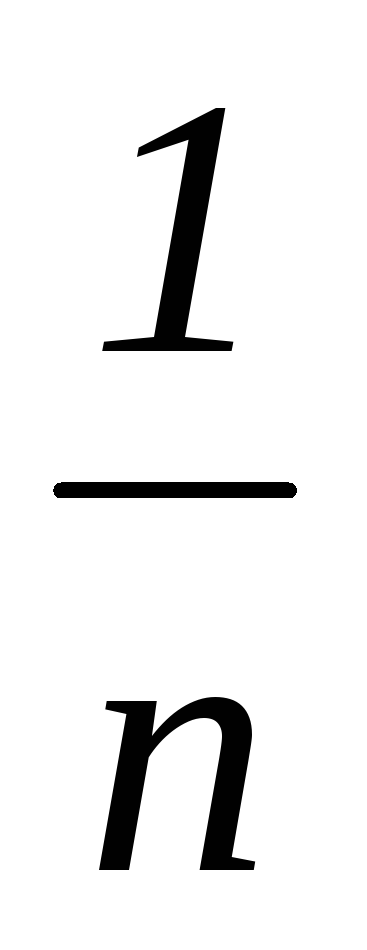
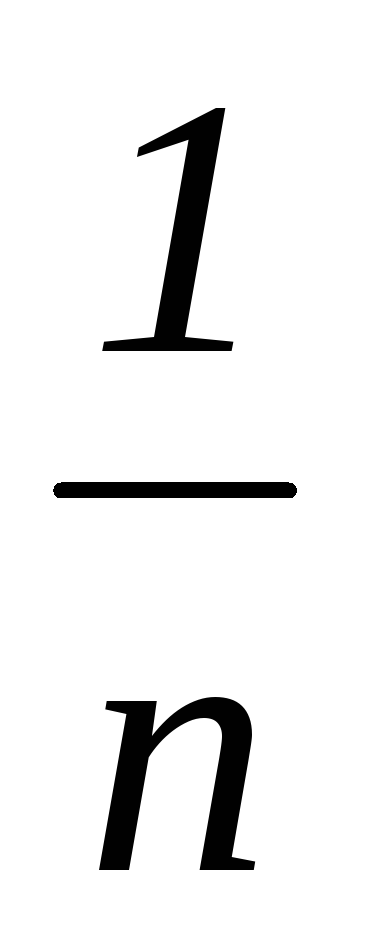
Применимы все законы и понятия теории вероятностей. Можно вычислить эмпирическую функцию распределения:

=

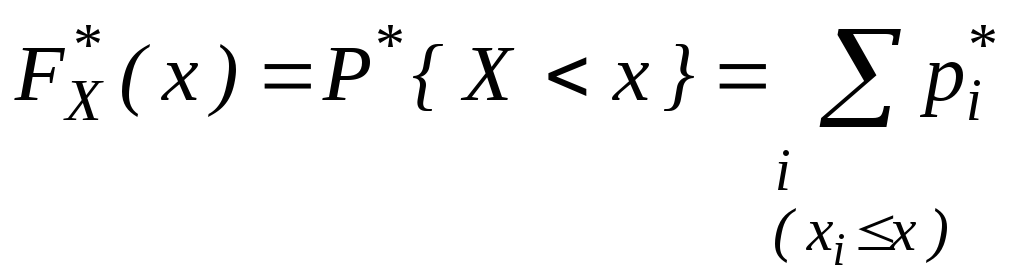Подсчитать можно только частоты .

Гистограмма.

Наибольшее значение имеет для интервалов визуальное представление вероятностей.

Выборочные характеристики (моменты)

1)

Частные случаи:

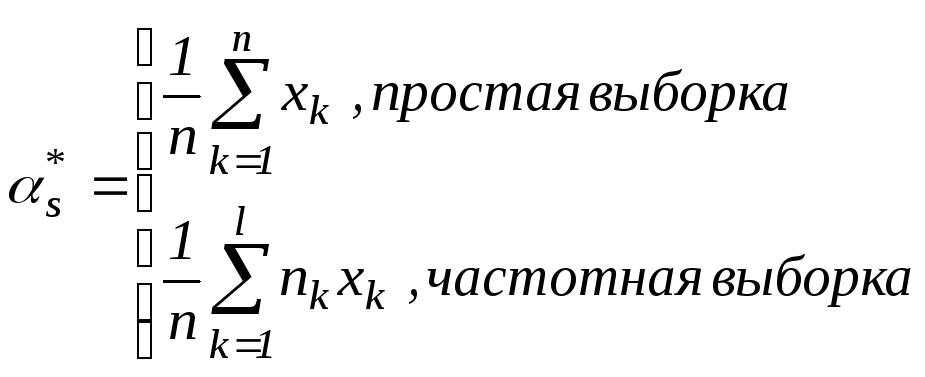
-среднеарифметическое выборочное (аналог математического ожидания).

2)

3) Мода выборочного распределения - аргумент максимума

4) Медиана (только для дискретного распределения):

 корень уравнения . Слева и справа от должно быть одинаковое количество значений.

§6.3. Точечное оценивание неизвестных характеристик генерального.

Требования, предъявляемые к оценке: Пусть  - неизвестная характеристика генерального, - ее оценка по выборке. - случайная величина. должна обладать следующими свойствами:

1) несмещенность: .

Пояснение:  - - ошибка оценивания.

Пусть  -=.

M[случайной ошибки]=0

2) состоятельность:

Микротеорема (о достаточных условиях состоятельности). Пусть оценка удовлетворяет двум условиям:

1) несмещенная;

2) ;

Тогда - состоятельна.

P{|- | }=(в силу условия 1)=P{|-|  } (согласно второму неравенству Чебышева) . В силу условия 2) получаем , т.е. состоятельна, что и требовалось доказать.

3) отностительная эфективность

Пусть и - несмещенные оценки параметра  оценка - более эффективная, если

Методы получения оценок в точках. Проверка свойств.

1) Метод подстановки.

Пусть  - неизвестная моментная характеристика генерального  =^* для эмпирического распределения. (Например, и т.д.)

Пример 1. Пусть Х - имеет конечный M[X²]. Оценить m_X и проверить свойства.

По методу подстановки предписано: m_X=₁. Проверим свойства:

а) несмещенность.

== несмещенность доказана.

б) состоятельность.

Достаточно проверить условие 2) микротеоремы. ==0  состоятельность доказана.

Пример 2. Пусть Х имеет конечный M[X⁴]. Оценить неизвестные ₂ и ₂ и проверить их свойства.

Проверим свойства:

а) === несмещенная;

б) ==(в силу независимости)= = =()

в) оценим дисперсию: