Лекции / Лекции (МП-3 Земсков) / Лекции (word) / Лекци16

Лекция 16.

5.2. Центральная предельная теорема.

Теорема. Пусть для последовательности случайных величин Х₁, Х₂,.., Х_n выполняются условия:

1. при любых n случайные величины Х₁, Х₂,.., Х_n – независимы в совокупности;

2. одинаково распределены;

3. существует

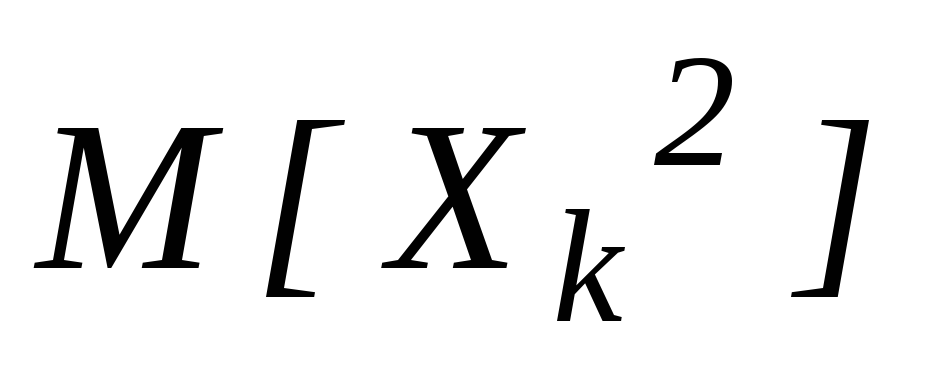
Обозначим:

, где

Тогда

(Подразумевается, что естественный закон будет нормальным)

Из условия (3) следует, что существует , .

Проверим, что - стандартизованная случайная величина.

Действительно,

=

=

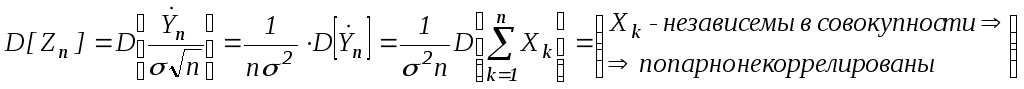Строим характеристическую функцию по этапам:

Заметим, что .

I этап. Ищем , т.к. по условию (3) существует 

 по свойству (4) характеристической функции существует и .

Тогда разложим функцию в ряд Тейлора до членов второго порядка включительно с остаточным членом в форме Пеано 

 (1)

(по свойству (1) характеристической функции);

;

Подставим это все в (1):

(2)

II этап. Так как (по свойству (3) характеристической функции) 

 (по формуле (2) ) =

III этап. ( по свойству (2) характеристической функции) =

=

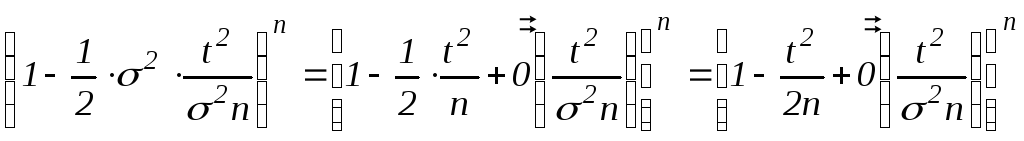
Итак, .

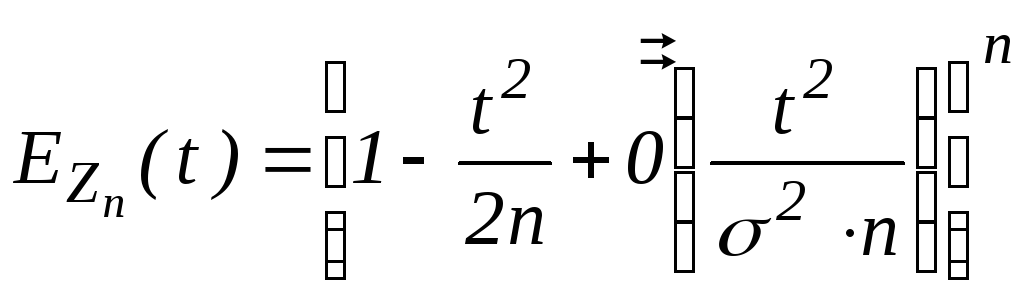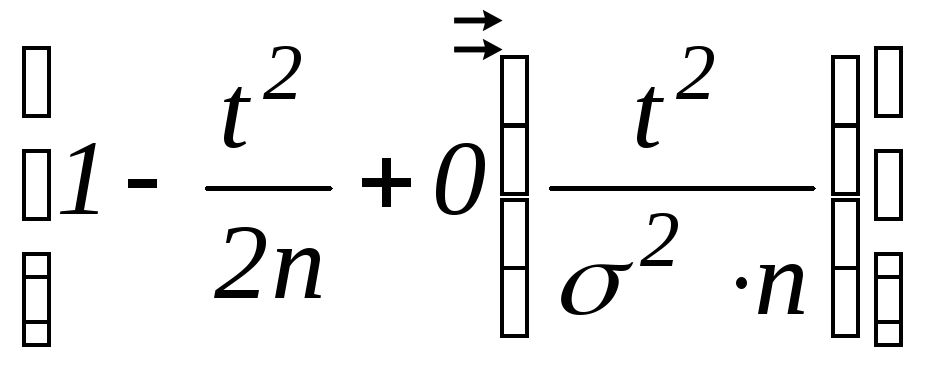=(, - малое)= = =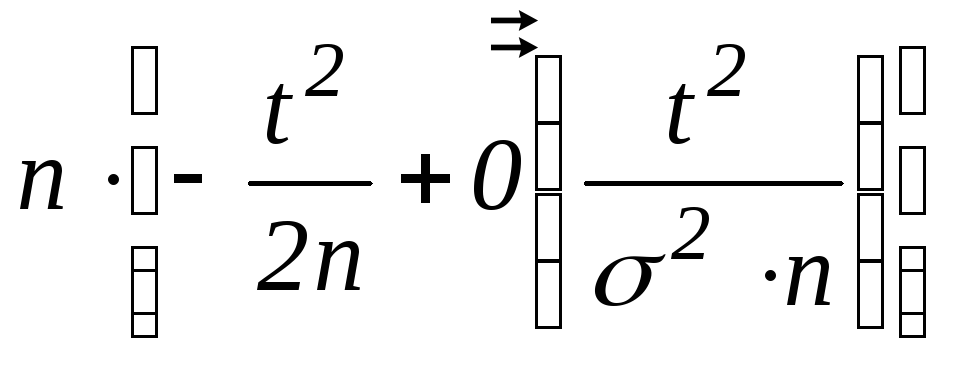

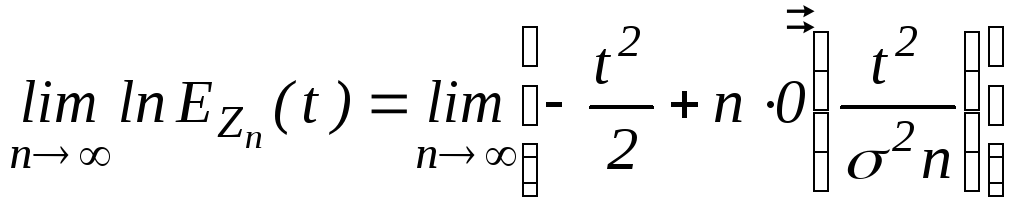Замечание. Мы дали одну из простейших формулировок центральной предельной теоремы. Все более поздние формулировки связаны с устранением пункта 2). Необходимо одинаковое распределение, но тогда усложняются условие 3). Чаще всего оно формулируется в виде условия Венде Берга (гарантирует, что все слагаемые Х_к вносят равномерно малый вклад в общую дисперсию)

Применение. 1) Баллистика.

2) Отклонение от нормали.

3) Статистика (ошибки распределений)

5.3. Следствия ЦПТ для схемы Бернулли.

Пусть ~B(n,p).

Известно, что , где I_k ~B(1,p) – индикатор успеха в n опытах по схеме Бернулли. Легко видеть, что последовательность I₁ ,I₂ ,…удовлетворяет ЦПТ. Можно утверждать, что если мы построим .

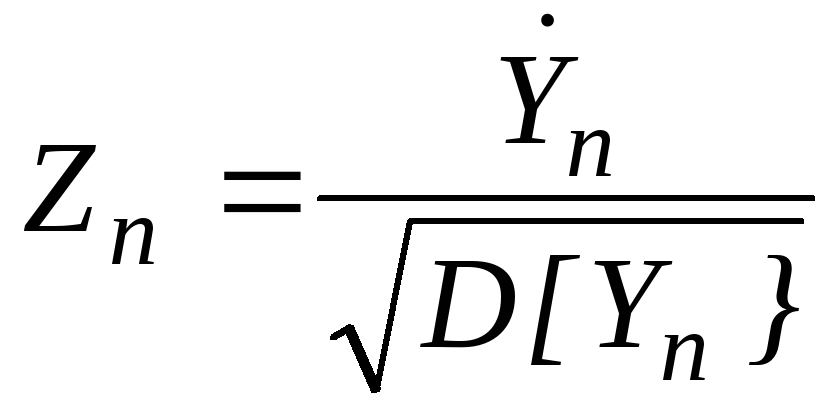Очевидно, что при достаточно больших n :

.

Воспользуемся общей оценкой.

Уточнение ЦПТ для конечных n приводит к неравенству:

(3)

Известно, что

Применим оценку (3) для схемы Бернулли. Роль Х_к выполняют I_k . Надо найти

Закон распределения I_k

Ik	0	1
p	q	p

Оценим правую часть в (3):

Тогда (4)

Локальная Теорема Муавра-Лапласа.

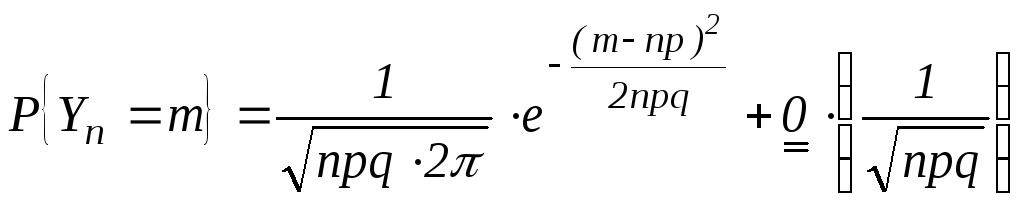(5)

Пример 1. Сделано 100 выстрелов с вероятностью попадания р=0,3. Вычислить вероятность .

={ число попаданий при n=100 выстрелов}

(важно, чтобы р не было очень маленьким)

npq=100  0,3  0,7 = 21

Ошибка имеет порядок

.

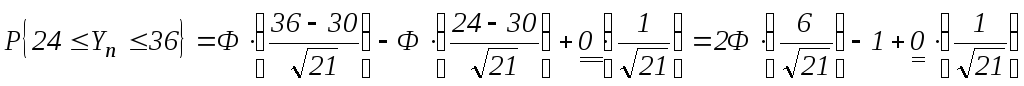
Точный ответ: 0,7578