Лаб.раб. по механике / ЛАБОРАТОРНАЯ РАБОТА №5

ЛАБОРАТОРНАЯ РАБОТА № 5

ОПРЕДЕЛЕНИЕ МОДУЛЯ СДВИГА

ЦЕЛЬ РАБОТЫ: экспериментальное определение модуля сдвига материала проволоки методом крутильных колебаний.

ОБОРУДОВАНИЕ: крутильный маятник, измерительные приборы.

КРАТКАЯ ТЕОРИЯ

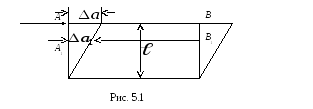
Деформация сдвига. Пусть имеется прямоугольный параллелепипед, нижняя грань которого закреплена, а к верхней грани приложена сила , ее называют скалывающей (рис. 5.1).

Отношение называется скалывающим усилием, оно равно силе, действующей на единицу площади поверхности верхней грани и направлено также по касательной к этой поверхности. Из рис. 5.1 видно, что под действием силы слои параллелепипеда начнут смещаться. Верхний слой сместится на величину ,более глубокие слои – на меньшую величину ,и т.д. Возникает деформация сдвига, которая приводит к появлению упругих сил в теле. Величина, определяемая соотношением, называется относительным сдвигом. Для малых углов сдвига и, следовательно, . Таким образом, при малой деформации относительный сдвиг равен углу сдвига в радианах. Опыт показывает, что абсолютный сдвиг определяется формулой , здесь - коэффициент сдвига, величина которого определяется упругими свойствами материала. На практике обычно пользуются другой величиной , называемой модулем сдвига. Следовательно, - относительный сдвиг пропорционален скалывающему усилию. При статических деформациях упругое напряжение равно и противоположно скалывающему усилию. Следовательно, - закон Гука: при небольших деформациях тангенциальное напряжение пропорционально относительному сдвигу. Можно показать, что величины объединяет соотношение . Это означает, что любую деформацию можно приводить к двум: либо к растяжению и сжатию с модулями , либо к растяжению (или сжатию) и сдвигу с модулями .

Деформация кручения.

Пусть имеется круглый стержень (или проволока) длиной и радиусом R (рис.5.2). Верхний конец этого стержня закреплен, а к нижнему приложен вращающий момент , где - некоторая вращающая сила. Тогда любой радиус незакрепленного конца повернется на некоторый угол , так как при кручении все поперечные слои подвергнутся деформации сдвига. Но эта деформация неоднородна, так как на различных расстояниях от места закрепления стержня угол поворота изменяется от нуля до максимального значения у свободного конца. Опыт показывает, что угол закручивания для упругой деформации пропорционален крутящему моменту φ~M или

(5.1)

Вычисления показывают, что момент сил связан с углом закручивания соотношением

. (5.2)

Здесь N – модуль сдвига материала стержня, - угол закручивания стержня на расстоянии от места закрепления, R – радиус стержня. Коэффициент зависит не только от материала стержня (через модуль сдвига ), но его геометрических размеров. Для данного стержня эта величина постоянная и называется модулем кручения. Из формулы (5.2) следует, что модуль кручения численно равен моменту сил, закручивающих данный стержень на угол .

ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА.

ТЕОРИЯ МЕТОДА И МЕТОДИКА ИЗМЕРЕНИЙ

Из формулы (5.2) следует два возможных метода экспериментального определения модуля сдвига:

1) Статический – в этом случае измеряется момент закручивающих сил и соответствующий ему угол закручивания;

2) Динамический – в этом случае, если закрученный на некоторый угол стержень освободить от действия вращающих сил, то возникшие в стержне упругие силы вызовут крутильные колебания стержня. Динамический метод не требует точной аппаратуры для измерения углов и моментов сил и находит широкое применение для экспериментального определения модуля сдвига. Как видно из формулы (5.2) для длинных и тонких нитей, на которые подвешивают колеблющееся устройство, нужен очень небольшой момент сил для закручивания нити на значительный угол. Этим обстоятельством пользуются при создании очень чувствительных измерительных приборов (так был с помощью крутильных весов открыт закон Кулона и впервые измерена гравитационная постоянная G – очень маленькая величина).

Схематическое устройство крутильного маятника изображено на рисунке 5.4. К нижнему концу проволоки из исследуемого материала прикреплен горизонтальный стержень АВ, на котором могут свободно передвигаться два одинаковых цилиндра. Для равновесия стержня АВ цилиндры располагаются симметрично относительно проволоки. Стержень АВ и цилиндры увеличивают инертность крутильного маятника, благодаря чему колебания становятся более заметными и продолжительными, а при изменении положения цилиндров на стержне меняется период крутильных колебаний маятника. Полученное устройство представляет собой один из видов физического маятника. Период его колебаний можно написать по аналогии с периодом пружинного маятника. Как известно, при колебаниях пружинного маятника массой на него действует упругая возвращающая сила , а период колебания равен . При колебаниях физического (крутильного) маятника на него действует возвращающий момент упругих сил , а период колебаний равен , здесь - момент инерции маятника (см. приложение). Учитывая формулу (5.2), можно написать окончательное выражение для периода . Итак, для двух положений цилиндров, находящихся на расстоянии и от оси вращения периоды колебания будут: и . Здесь - момент инерции прибора относительно оси вращения при положении цилиндров на расстоянии от оси вращения, - тоже для расстояния (см. приложение).

Из приведенных формул легко получить выражения для модуля кручения 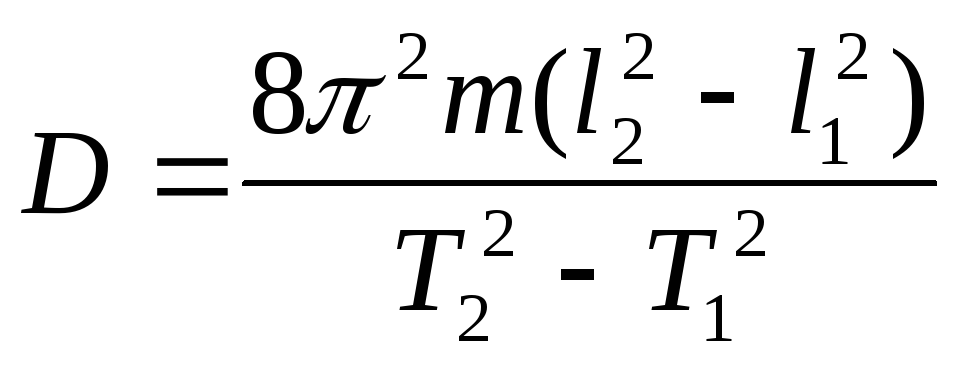и модуля сдвига .

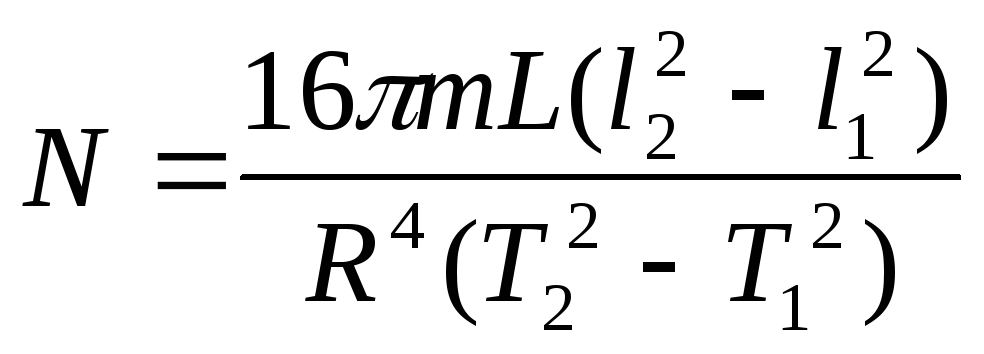ЗАДАНИЯ

1. Изучите теорию данного вопроса и ответьте на контрольные вопросы.

2. Изучите экспериментальную установку и порядок работы на ней.

3. Измерьте массу цилиндров и размеры проволоки.

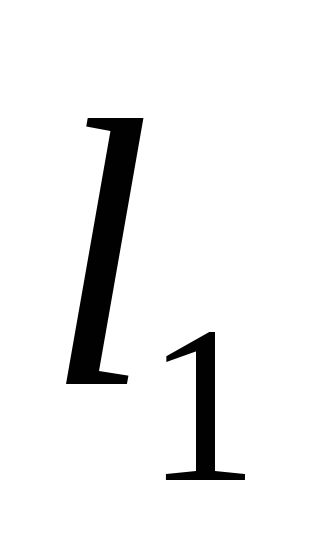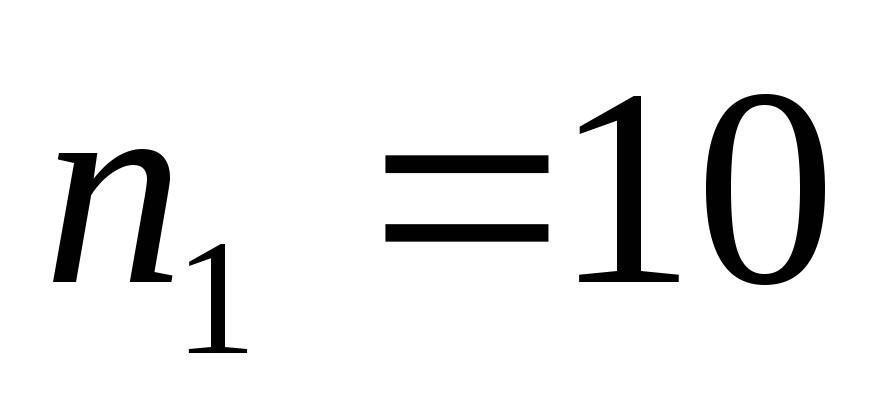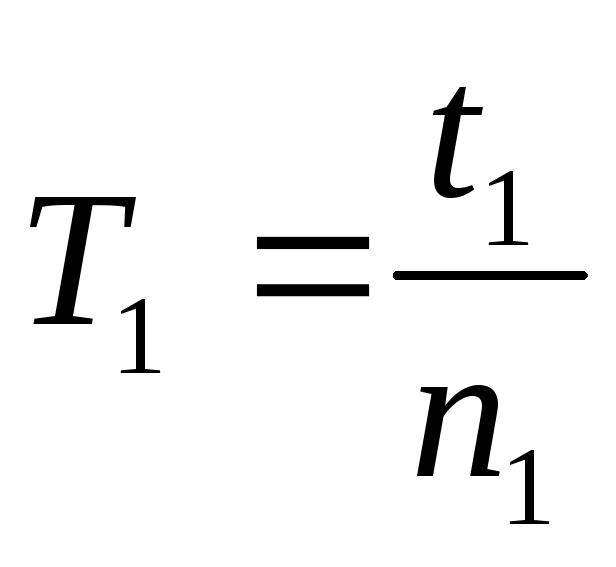4. Установите цилиндры на некоторое расстояние . Осторожно отклоните стержень АВ на некоторый небольшой угол и подсчитайте время , например, и колебаний. Определите период колебаний и 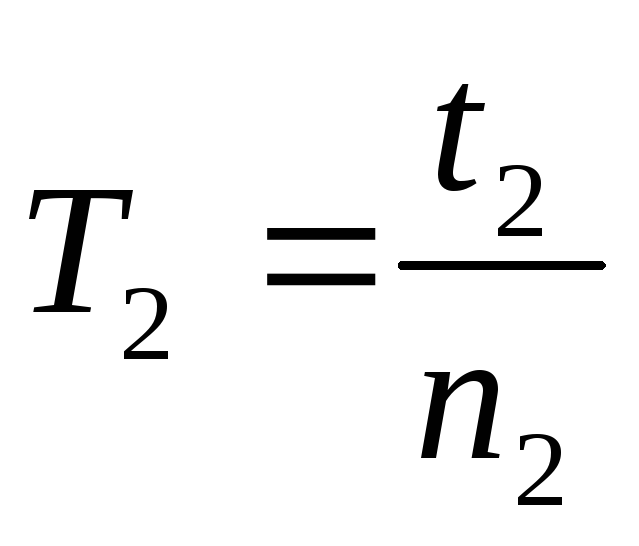. Затем отклоните стержень на другой несколько больший угол и проделайте те же измерения. Дело в том, что изложенная теория создана для малых незатухающих колебаний. В данной работе колебания конечно же затухающие. Кроме того заранее трудно сказать являются ли колебания малыми. Если полученные четыре периода будут отличаться незначительно (единицы процентов), то условие малости и слабого затухания будет выполнено. Если, например, для колебаний период будет значительно отличаться от 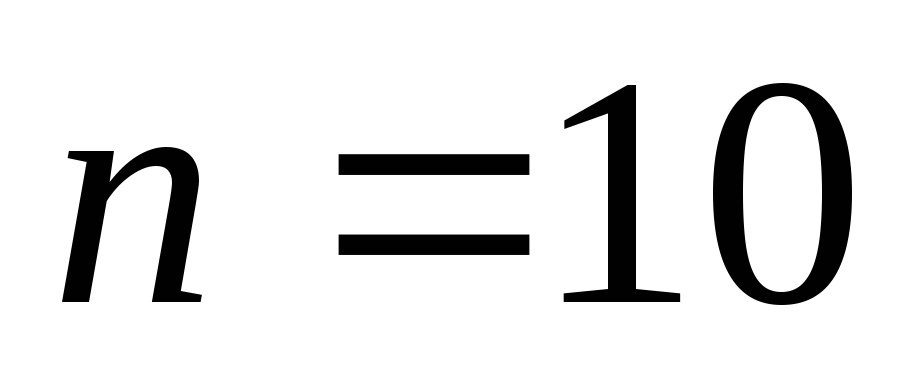, то определять период за большое число колебаний нельзя (а за малое число будет большая погрешность).

5. Аналогично измерить период колебаний для расстояния .

6. Вычислите модуль сдвига 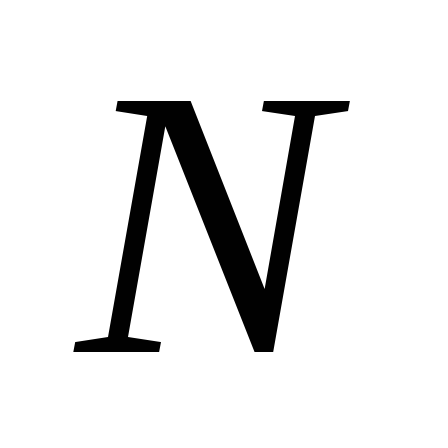, оцените погрешность измерений и сравните полученный результат с табличным.

7. Проделайте такие же измерения и расчеты для проволоки из другого материала.

ОПРЕДЕЛЕНИЕ МОДУЛЯ СДВИГИ ПРИ ПОМОЩИ

КРУТИЛЬНЫХ КОЛЕБАНИЙ КОЛЬЦА

ТЕОРИЯ МЕТОДА И МЕТОДИКА ИЗМЕРЕНИЙ

К концу проволоки вместо стержня прикрепляют массивный диск, расположенный горизонтально. На диск кладут кольцо так, чтобы его центр находился на оси вращения системы. Период крутильных колебаний измеряют также как в предыдущем случае дважды: без кольца и с кольцом. Периоды колебаний рассчитываются по формулам и . Здесь - момент инерции диска; - момент инерции системы диск-кольцо.

Здесь ; ; и - массы диска и кольца соответственно; - радиусы диска и кольца (внутренний и внешний).

Из приведенных соотношений получаем

Задание: произвести измерения и подсчеты также, как в предыдущем случае.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какая деформация называется упругой?

2. Что такое предел упругости и предел прочности?

3. Сформулируйте закон Гука для деформации растяжения, сдвига и кручения. Каков физический смысл величин, входящих в формулы закона Гука?

4. Почему в крутильном маятнике стержень, цилиндры, диск и кольцо должны быть достаточно тяжелыми (но не слишком тяжелыми)?

5. Как надо выбирать расстояния и ?

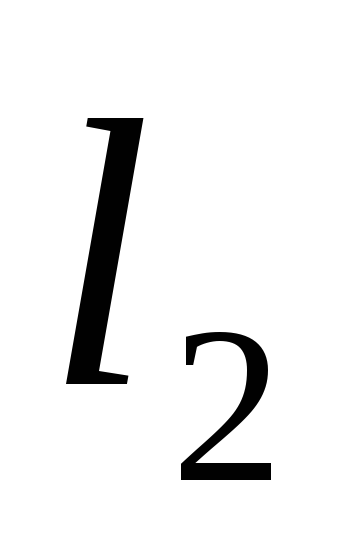6. Что такое физический маятник? Как определяется его период колебаний?

7. Что такое момент силы и момент инерции тела?

8. В чем заключается теорема Штейнера?

ПРИЛОЖЕНИЕ

Как известно, при прямолинейном движении тела его инертные свойства (способность сохранять покой или движение без изменения) определяются массой. При вращательном движении для характеристики этого свойства одной массы недостаточно. Оказывается надо знать еще как она распределена в теле относительно оси вращения. Для этого вводится новая характеристика – момент инерции тела относительно оси вращения. Для простейшего объекта – материальной точки момент инерции относительно оси вращения равен . Из этой формулы следует, что чем дальше материальная точка будет находиться от оси вращения (т.е. чем больше ), тем больше ее инертность во вращательном движении (при неизменной массе). Момент инерции твердого тела как системы материальных точек естественно определить соотношением . Здесь - масса материальной точки, находящейся на расстоянии от оси вращения. Для практического вычисления моментов инерции эта формула неудобна. Методами дифференциального и интегрального исчисления можно показать, что моменты инерции наиболее часто встречающихся тел равны:

1. Сплошного диска ;

2. Тонкостенного кольца (обода) ;

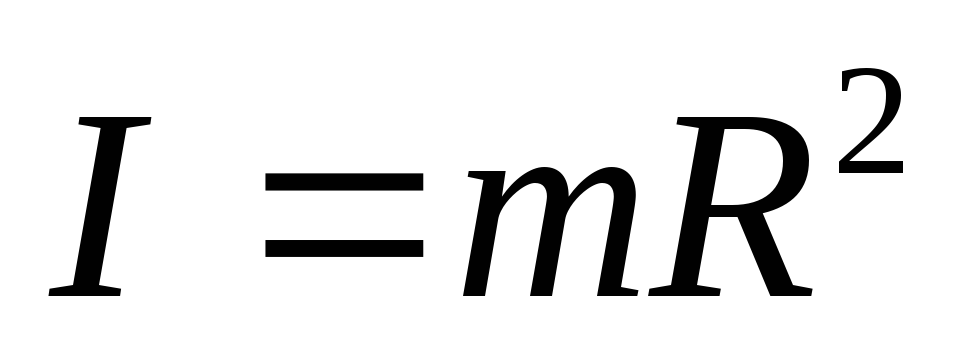3. Толстого кольца (как в данной работе) . Здесь и - внутренний и внешний радиусы.

Все приведенные формулы определяют момент инерции относительно оси, проходящей через центр масс (геометрический центр) тел. Но часто приходится находить момент инерции относительно оси, параллельной вышеуказанной, находящейся на расстоянии от первой. В этом случае для нахождения момента инерции используется теорема Штейнера . Здесь - момент инерции тела относительно оси, проходящей через центр масс тела, - момент инерции относительно оси, находящейся на расстоянии от первой, - масса тела.

В данной работе приводится формула для момента инерции крутильного маятника. Если бы цилиндр был в положении, указанном на рис 5.3, то момент инерции установки был бы равен . Здесь - момент инерции стержня и - момент инерции цилиндра относительно оси, совпадающей с проволокой (их явные выражения не нужны). При смещении цилиндров на расстояние (рис.5.4) момент инерции установки в соответствии с теоремой Штейнера будет равен ; для расстояния будет . Коэффициент 2 появляется из-за того, что цилиндров 2.

Формулы для момента инерции крутильного маятника с диском и кольцом очевидны.