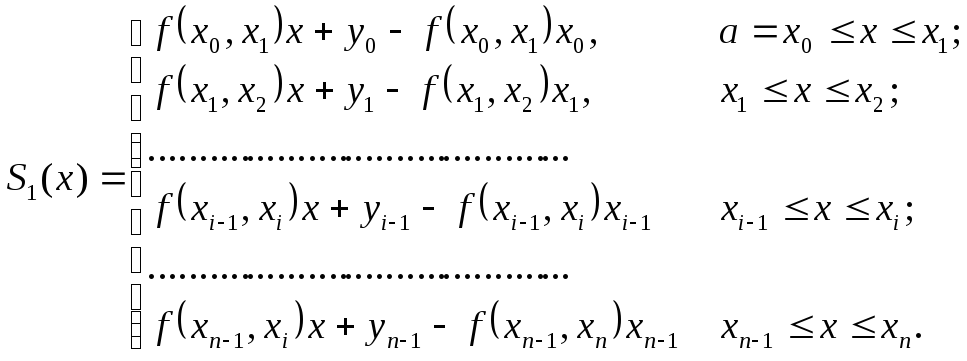МатМод2Г / Самостоятельно / Интерполирование сплайнами (кратко)

Интерполирование сплайнами

Остановимся на рассмотрении интерполирования полиномиальными сплайнами. Задача интерполирования полиномиальным сплайном состоит в следующем:

Пусть в точках a=x₀<x₁<…<x_n=b заданы значения функции f(x):

f(x₀)=y₀, f(x₁)=y₁, … , f(x_n)=y_n.

Необходимо найти функцию S_m(x), удовлетворяющую требованиям:

1. на каждом из отрезков [x_i-1, x_i] S_m(x) является многочленом степени m

   Smi(x)=a0ixm+ a1ixm-1+…+ am-1,ix+ ami,   xi-1x xi,  i=1,2, …,n;

2. в точках x_i имеют место равенства

   Sm(xi)= f(xi)=yi,  i=0,1, …,n (условие интерполяции);

3. S_m(x) непрерывна и имеет непрерывные производные до (m‑1)‑го порядка, т.е.

, i=1,2, …,n, j=0,1,…,m

(условия непрерывности).

Функция S_m(x) называется полиномиальным сплайном порядка m. В дальнейшем для краткости будем называть ее просто сплайн.

Итак, чтобы построить интерполяционный сплайн S_m(x) необходимо найти n(m+1) коэффициентов a_ki, k=0,1,…,m, i=1,2, …,n. Для чего по условиям (2) и (3) составляют систему линейных алгебраических уравнений. Условие (2) дает n+1 уравнение, а условие (3)  m(n1) уравнений. Недостающие m1 уравнение получают, налагая дополнительные краевые условия, т.е. условия в точках a и b.

Можно доказать, что полученная таким образом система линейных алгебраических уравнений определяет единственный сплайн степени m S_m(x), интерполирующий функцию f(x) в заданных узлах интерполяции.

На практике чаще всего применяют сплайны 3-его порядка, называемые кубическими, так как это сплайны минимальной степени, имеющие непрерывную вторую производную, что является необходимым требованием при проектировании кривых. Это значит, что на каждом из отрезков [x_i-1, x_i], i=1,2, …,n функцию f(x) заменяют кубическим многочленом S_3i(x), принимающим на концах отрезка значения S_3i(x_i-1)=f(x_i-1)=y_i-1 и S_3i(x_i)=f(x_i)=y_i соответственно, причем и , i=1, 2, …, n. Дополнительные краевые условия могут быть, например, такими: и (можно задать и другие краевые условия).

Задача построения кубического сплайна сводится к решению системы линейных алгебраических уравнений с симметричной матрицей коэффициентов, со строгим диагональным преобладанием, т.е. в каждой строке модуль диагонального элемента больше суммы модулей остальных элементов. В линейной алгебре доказывается, что система с такой матрицей имеет единственное решение. Кроме того, матрица коэффициентов системы является трехдиагональной, т.е. ненулевыми в ней являются только элементы главной и двух соседних ей диагоналей. Решение такой системы находят методом прогонки, который является частным случаем метода Гаусса, учитывающим специальный вид матрицы системы.

На практике иногда применяют интерполирование сплайном первого порядка S₁(x). Оно состоит в замене графика функции f(x) ломаной, построенной по узлам. Для построения такой ломаной, необходимо найти коэффициенты прямых, проходящих через точки (x_i, y_i) и (x_i, y_i):

или

, i=1,2, …,n.

Таким образом, с учетом обозначения , имеем