МатМод2Г / Самостоятельно / Отделение корней уравнения

Некоторые приемы отделения корней уравнения.

Определение

Корень уравнения F(x) = 0 считается отделенным на отрезке [a, b], если на этом отрезке нет других корней.

Существует большой набор приемов и теорем, помогающие это сделать, но единой теории не существует.

Корни отделяются просто, если можно построить график функции f(x). Точки пересечения графика с осью Оx дают значения корней, и по графику легко определить два числа a и b, между которыми заключен только один корень.

Пример 1. Отделить корни уравнения x³-3x-1=0.

 Построим график функции y = x3-3x-1 (рис.1). Кривая пересекает ось Оx в трех точках. Следовательно, уравнение имеет три действительных корня с1 , с2 , с3. Из чертежа видно, что с1[-2,1], с2[-1,0], с3[1,2] 
	Рис.1.

Если построение графика y = f(x) вызывает затруднение, то уравнение (1) преобразовывают к виду f₁(x) = f₂(x) так, чтобы графики функций f₁(x) и f₂(x) было легко построить. Абсциссы точек пересечения этих графиков и являются корнями уравнения. По графику определяют два числа a и b, между которыми заключен корень.

Пример 2. Отделить корни уравнения x - cos x = 0 .

 Перепишем уравнение в виде: x = cos x и построим графики функций y = x и y = cos x в промежутке [-,] (рис.2). Графики функций пересекаются в одной точке. Учитывая свойства функ-ций можно утверждать, что вне этого промежутка данное уравнение корней не имеет. Таким образом, c [ 0,/2].
	Рис.2.

Рассмотренный способ отделения корней будем называть графическим.

Корни уравнения (1) можно отделить, используя приемы анализа функций, известные из курса математического анализа. Ниже приведены некоторые теоремы, знание которых необходимо при отделении корней.

Теорема 1 (о существовании нуля функции)
	Если функция f(x) непрерывна на отрезке [a,b] и на его концах принимает значения разного знака, то есть f(a)f(b)<0, то внутри отрезка существует хотя бы одна точка, в которой функция f(x) обращается в нуль.

Проиллюстрируем теорему графически:

f(a)>0; f(b)<0. Рис.3.

Теорема 2 (о существовании и единственности нуля функции).
	Если функция f(x) непрерывна на отрезке [a,b], принимает на его концах значения разного знака, то есть f(a) f(b) < 0, и первая производная f(x) сохраняет постоянный знак на интервале (a,b), то на этом интервале существует точка - и при том единственная - в которой функция f(x) обращается в нуль.

Проиллюстрируем теорему графически:

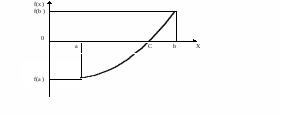
Рис.4. f(a)<0, f(b)>0; f(x)>0.	Рис.5. f(a)>0, f(b)<0; f(x)<0.

Пример 3. Отделить корни уравнения 5^x - 6x - 3 = 0.

 Проведем аналитическое исследование заданной функции.

Функция f(x) = 5^x - 6x - 3 определена и непрерывна на всей числовой прямой. Находим первую производную f(x)= 5^x ln 5- 6 и выделяем промежутки, внутри которых первая производная сохраняет знак. Для этого находим точки, в которых производная обращается в нуль:

5^x ln 5 - 6 = 0;

5^x = 6 / ln 5;

x ln 5 = ln 6 - ln(ln 5);

x = (ln 6 - ln(ln 5))/ ln 5  (1.7918- 0.4759)/1.6094  0.8176;

Найденная точка делит числовую ось на два промежутка. Если значения функции на концах этих промежутков имеют противоположные знаки, то по теореме 2 каждый из них содержит корень уравнения и при том только один. Составим таблицу знаков функции на концах выделенных промежутков:

x	- 	0.8176	+ 
знак f(x)	+		+

Следовательно, уравнение имеет два действительных корня, заключенных в промежутках: (- , 0.8176) , (0.8176, + ).

Сузим каждый промежуток так, чтобы его границы были конечными:

x	- 1	0	0.8176	1	2
знак f(x)	+				+

Итак, уравнение имеет два действительных корня: с₁ [-1, 0 ], с₂ [1, 2].

Рассмотренный способ отделения корней будем называть аналитическим.

Замечание.  Если оказалось, что функция f(x) в области определения не меняет знак, то это значит, что уравнение либо не имеет корней, либо имеет корень четной кратности, либо имеет четное число близлежащих корней. 

Для полиномов, т.е. когда F(x) = P_n(x)= a_nxⁿ + a_{n -1} x^n-1 +  + a₁x + a₀ , таких вспомогательных теорем гораздо больше.

Теорема 3 (Основная теорема алгебры).
	У всякого многочлена Pn(x) степени не ниже первой с произвольными коэффициентами (действительными или комплексными) число корней - с учетом их кратности - равно степени многочлена.

В данном случае учитываются все корни - как действительные, так и комплексные. Поэтому следует не забывать, что комплексные корни всегда попарно сопряженные.

Теорема 4 (теорема Декарта).

Количество действительных положительных корней уравнения Pn(x)= 0 - с учетом их кратности - либо равно числу перемен знака в последовательности коэффициентов полинома Pn(x) уравнения, либо на четное число меньше. Количество действительных отрицательных корней уравнения - с учетом их кратности - либо равно числу перемен знака в последовательности коэффициентов полинома Pn(-x), либо на четное число меньше.

При составлении последовательности коэффициентов, свободный член учитывается, а равные нулю коэффициенты не учитываются.

Пример 4. Отделить корни уравнения x³ - 6x² +20 = 0.

 По основной теореме алгебры уравнение может иметь не более трех действительных корней. Для их отделения воспользуемся теоремой Декарта.

Выпишем последовательность коэффициентов заданного полинома:

коэффициент	1	6	+20
знак коэффициента	+		+	две смены знака

Следовательно, положительных действительных корней не более двух.

Теперь выпишем последовательность коэффициентов полинома

P₃ (-x)= - x³ - 6x² +20:

коэффициент	1	6	+20
знак коэффициента			+	одна смена знака

Следовательно, отрицательных действительных корней не более одного.

Полином P₃ (x)= x³ - 6x²+ 20 определен и непрерывен на всей числовой прямой. Находим первую производную P₃(x) = 3x²- 2x=3x(x-4) и выделяем промежутки, внутри которых первая производная сохраняет знак:

x	(- , 0)	(0, 4)	(4, + )
знак P3(x)	+		+

Сузим промежутки так, чтобы их границы были конечными и найдем значение полинома на концах промежутков:

x	- 2	(-2, 0)	0	(0, 4)	4	(4, 6)	6
P3(x)	-12		20		-12		20
знак P3(x)	+	+	0		0	+	+

Итак, уравнение имеет три действительных корня:

с₁(-2, 0 ), с₂( 0, 4), с₃(4, 6).

Пример 5. Отделить корни уравнения x⁵ + 3x⁴ - x³ -1 = 0.

 По основной теореме алгебры уравнение может иметь не более пяти действительных корней. Для их отделения воспользуемся теоремой Декарта.

Выпишем последовательность коэффициентов заданного полинома:

коэффициент	1	+3	1	1
знак коэффициента	+	+			одна смена знака

Следовательно, положительных действительных корней не более одного.

Теперь выпишем последовательность коэффициентов полинома

P₅(-x)= - x⁵ + 3x⁴ + x³ -1:

коэффициент	1	+3	+1	1
знак коэффициента		+	+		две смены знака

Следовательно, отрицательных действительных корней не более двух.

Значит данное уравнение может иметь не более трех действительных корней. Определим, где они находятся.

Полином P₅(x)= x⁵ + 3x⁴ - x³ -1 определен и непрерывен на всей числовой прямой.

Перепишем уравнение в виде: x² + 3x- 1= 1/x³ и построим графики функций

f₁ =x² + 3x - 1=(x+3/2)² - 13/4 и f₂ = 1/ x³. Графики функций пересекаются в трех точках.

Рис.6.

По графику определяем, что корни уравнения заключены в промежутках:

с₁(-4,-3), с₂(-1, 0 ), с₃( 0, 1).