Метод хорд

Пусть уравнение

f(x)=0

имеет на отрезке [a,b] единственный корень c, значение которого необходимо найти с заданной точностью , >0.

Заменим уравнение (1) эквивалентным ему уравнением

x=x-(x)f(x)

где (x) – непрерывна на отрезке [a,b] и не имеет корней на этом отрезке. Выберем в качестве функции (x) функцию

, где x^*[a,b] и не является корнем уравнения (1).

Тогда (2) примет вид:

Построим последовательность

, n=0, 1, 2, …

Воспользовавшись условием сходимости итерационных методом, аналогично тому как это было сделано для метода Ньютона можно доказать, что существует такая окрестность X корня c, что выбрав x₀X, получим итерационную последовательность (3), сходящуюся к корню c. И опять возникает проблема выбора начального приближения x₀, для разрешения которой рассмотрим геометрическую интерпретацию метода, выделив при этом четыре случая поведения функции f(x) на отрезке [a,b]:

1. f’(x)>0, f”(x)>0;

2. f’(x)<0, f”(x)>0;

3. f’(x)>0, f”(x)<0;

4. f’(x)<0, f”(x)<0.

Остановимся на первом из них. Пусть f’(x)>0 и f”(x)>0, то есть функция монотонно возрастает и выпукла вниз (вогнута вверх)

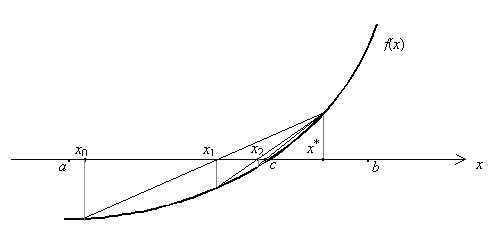
Выберем x^* справа от корня c, а x₀ слева от корня c, то есть c<x^*b, ax₀<c. Через точки (x₀, f(x₀)) и (x^*, f(x^*)) проведем прямую и точку пересечения ее с осью Ox обозначим x₁. Через точки (x₁, f(x₁)) и (x^*, f(x^*)) снова проведем прямую, точку пересечения которой с осью Ox обозначим x₂ и так далее.

Уравнение прямой, проходящей через точки (x_n, f(x_n)) и (x^*, f(x^*)), n=0, 1, 2,… имеет вид:

Тогда для точки пересечения этой прямой с осью Ox (x_n+1,0) имеем

Откуда

.

То есть получили формулу (3).

Таким образом, геометрически метод хорд состоит в замене на каждой итерации дуги кривой y=f(x) отрезком прямой (хордой), соединяющей некоторую фиксированную точку (x^*, f(x^*)) с точкой (x_n, f(x_n)), n=0, 1, 2,… Точка пересечения ее с осью Ox x_n+1, n=0, 1, 2,… является очередным (n+1)-ым приближением к корню. При этом, если x^*выбрать справа от корня c, а x₀ слева от корня c, то есть c<x^*b, ax₀<c, то последовательность (3) монотонно возрастает и ограничена снизу, а значит сходится. Если же x^*выбрать слева от корня c, а x₀ справа от корня c, то есть ax^*<c, c<x₀b, то последовательность (3) может расходиться, что демонстрирует приведенный ниже рисунок

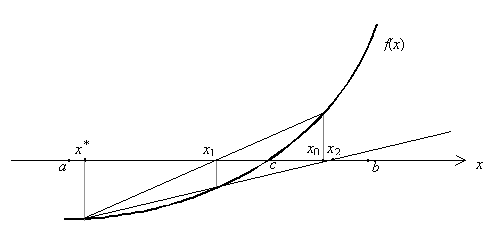
Докажем это.

Выясним, как точка x₁ располагается относительно точки x₀, то есть определим знак разности x₁-x₀. Из (3) имеем

то есть

и если c<x^*b ( f(x^*)>0) и ax₀<c (f(x₀)>0), то x₁>x₀, а если ax^*<c ( f(x^*)<0) и c<x₀b ( f(x₀)>0), то x₁<x₀

Выясним, как точка x₁ располагается относительно точки c, то есть определим знак разности x₁-с. Используя (3), найдем

Добавим в правую часть равенства f(c), равное нулю,

Применим к разностям значений функции f(x) и ее производной теорему Лагранжа о среднем¹

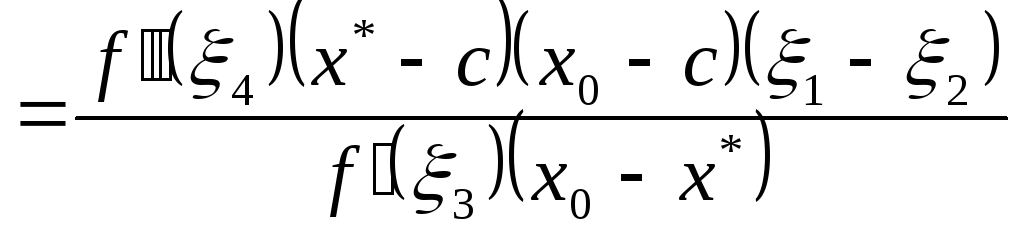
Окончательно имеем

,

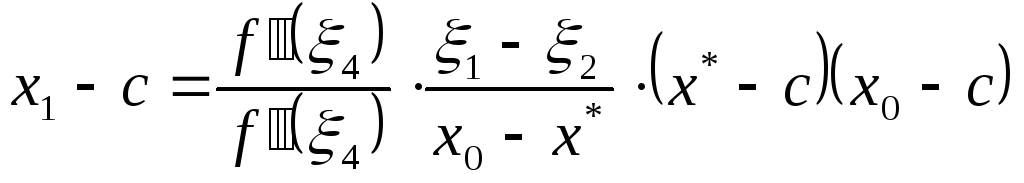где ₁ находится между x₀ и c, ₂ находится между x^* и c, ₃, ₄[a,b] (так как находятся между точками x₀, x^* и ₁, ₂ соответственно). И так как f’(x)>0 и f”(x)>0, x₀ и x^* располагаются по разные стороны от корня и₁ располагается по отношению к ₂ также как x₀ по отношению к x^*, то x₁<c.

Таким образом, если c<x^*b и ax₀<c, то x₀<x₁<c<x*.

Если же ax^*<c и c<x₀b, то x₁<x₀ и x₁<c и в этом случае необходимо выяснить, как точка x₁ располагается относительно точки x^*, то есть определить знак разности x₁-x^*. Используя (3), найдем

.

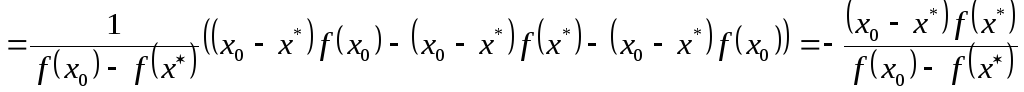Окончательно имеем

Таким образом, если ax^*<c ( f(x^*)<0) и c<x₀b ( f(x₀)>0), то x^*<x₁<c<x₀.

Далее доказательство проведем по индукции.

Выясним, как точка x₂ располагается относительно точек x₁ и c, то есть определить знаки разностей x₂-x₁ и x₂-с. Выполнив преобразования, аналогичные приведенным выше, получим

и так как ax₁<c (f(x₁)>0), то x₂>x₁,

,

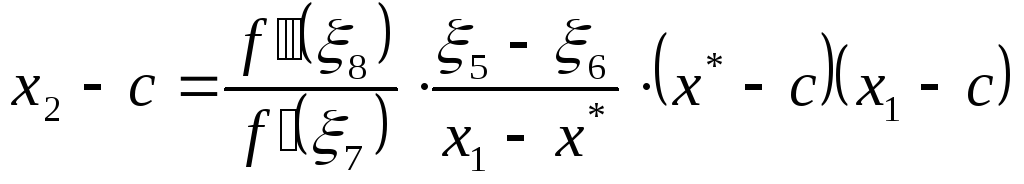где ₅ находится между x₁ и c, ₆ находится между x^* и c, ₇, ₈[a,b] (так как находятся между точками x₁, x^* и ₅, ₆ соответственно).

Таким образом, если c<x^*b и ax₀<c, то x₀<x₁<x₂<c<x*.

Если же ax^*<c и c<x₀b, то x₁<c<x₂ и исходя из графических соображений может оказаться, что x₂> x₀.

Пусть ax₀<x₁<x₂<…< x_n-1<c<x*b. Докажем, что x_n-1< x_n<c., то есть выясним, как точка x_n располагается относительно точек x_n-1 и c. Выполнив преобразования, аналогичные приведенным выше, получим

и так как ax_n-1<c (f(x_n-1)>0), то x_n>x_n-1,

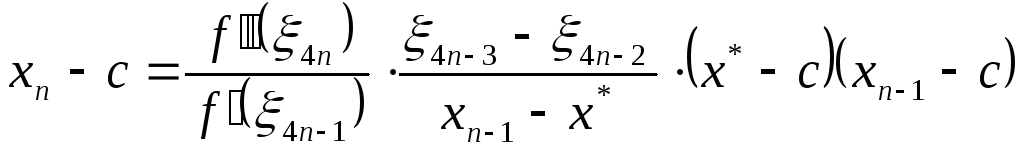, где _4n-3(x_n-1,c), _4n-2(c,x^*), _4n-1(x_n-1,x^*), _4n-3(_4n-3, _4n-2), и так как x_n-1<c<x^*, то x_n-1<x_n<c.

Таким образом, если f’(x)>0 и f”(x)>0 и x^*выбрать справа от корня c, а x₀ слева от корня c, то ax₀<x₁<x₂<…<x_n…<c<x*b, то есть последовательность (3) монотонно возрастает и ограничена снизу, а значит сходится.

Проведя в случаях II-IV аналогичные рассуждения, приходим к выводу:

Если функция f(x) непрерывна на отрезке [a,b] вместе со своими первой f’(x) и второй f”(x) производными, сохраняющими постоянный знак на этом отрезке, то выбрав x^*[a,b] и x₀[a,b] так, что f(x^*) f(x₀)<0 и f(x₁) f(x₀)>0 получим монотонную итерационную последовательность (3), сходящуюся к корню уравнения (1).

Для оценки погрешности метода хорд можно использовать полученную выше общую формулу оценки погрешностей итерационных методов, но для этого необходимо подобрать q, что в данном случае сделать затруднительно. Поэтому получим формулу для оценки погрешности метода хорд другим способом.

Из (3) имеем

Прибавим к левой части равенства f(c), равное нулю, а к дроби справа применим теорему Лагранжа о среднем

, где ₁ находится между x_n и x^*

Применив теорему Лагранжа о среднем к левой части равенства, получим

, где ₂ находится между x_n и с

К разности в скобках левой части равенства прибавим и вычтем x_n+1

;

.

Откуда

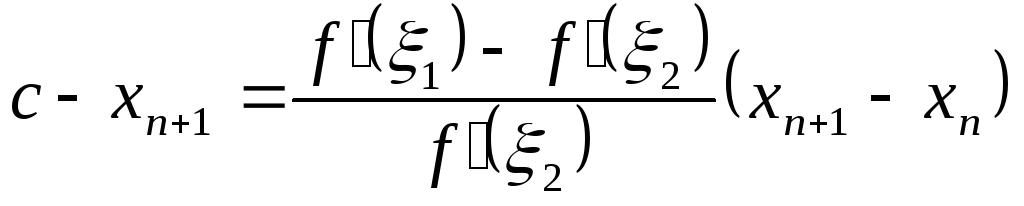
и

,

и так как f^’(x) сохраняет знак на отрезке [a,b] и ₁, ₂[a,b], то |f^’(₁)-f^’(₂)|M₁-m₁, где , и

,

то есть требуемая точность будет достигнута, если

или

1 Теорема Лагранжа о среднем. Если функция f(x)=0 непрерывна на отрезке [a,b] и в каждой точке интервала (a,b) имеет конечную или бесконечную определенного знака производную, то существует, по крайней мере, одна точка (a,b) такая, что f(b)– f(a)= f’()(b–a).