Лекции / 16

Вопрос 16. Статистическая проверка непараметрических гипотез.

Будем считать, что закон распределения генеральной совокупности неизвестен. Пусть из генеральной совокупности объемом n извлечена выборка. По виду полигона или гистограммы относительных частот всегда можно высказать гипотезу о законе распределения выборки, а, значит, и генеральной совокупности.

О1.Нулевой непараметрической гипотезой называется гипотеза об общем виде функции распределения H₀: F(x) = F₀(x).

Проверка гипотезы о предполагаемом распределении производится с помощью непараметрических критериев значимости. Способ построения таких критериев и методика их применения для проверки непараметрических гипотез такая же, как и для параметрических, т.е. проверка непараметрических гипотез производится на основании вычисления значения некоторой выборочной статистики или критерия, распределение, которое получено в предположении истинности H₀ и сравнении наблюдаемого значения с критическими.

Непараметрический критерий значимости можно разделить на:

1. критерий согласия, с помощью которого проверяется гипотеза об общем виде функции распределения. Наиболее распространенные из них ­­­– это критерий согласия χ²-Пирсона и λ-критерий Колмогорова;

2. критерии, с помощью которых проверяется гипотеза о принадлежности двух выборок одной и той же генеральной совокупности.

С помощью критериев первой группы можно проверить гипотезу о любом виде функции распределения (Пуассона, показательное, биномиальное, нормальное и др.). Однако, наиболее часто проверяется гипотеза о нормальном распределении.

Критерий согласия хи-квадрат (критэрий Пирсона), его применение к проверке статистических гипотез.

Пусть из генеральной совокупности извлечена выборка n50, а СВ имеет функцию распределения F(x).По данной выборке составлена таблица частот

			……..
			………

.

Требуется проверить нулевую гипотезу о том ,что модельная ф-я F(x) значимо представляет выборку, т.е. .При проверки этой гипотезы с помощью

критерия согласия Пирсона пользуются следующей схемой:

1. находят вероятности попадания СВ в частичный интервал

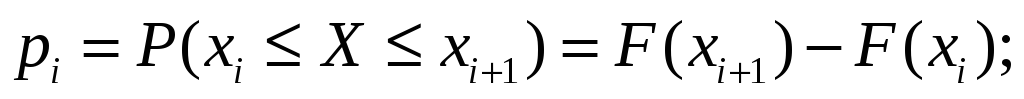
2. вычисляют теоретические частоты ,которые можно ожидать, если нулевая гипотеза справедлива;

3. находят наблюдаемое значение критерия, которое равно:

4. находят критическое значение критерия с помощью таблицы значений 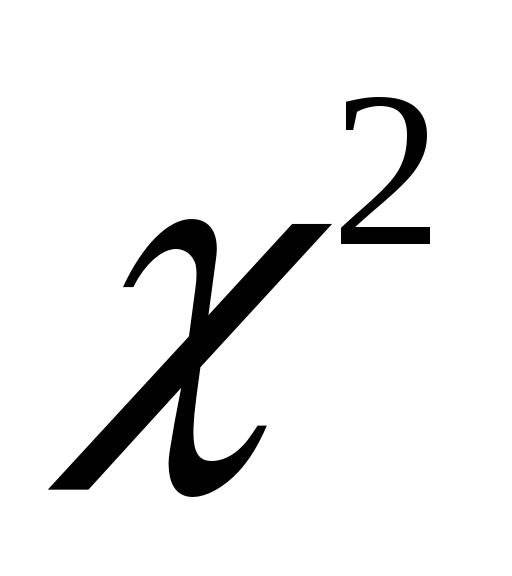(хи-квадрат) по уровню значимости и числу степеней свободы 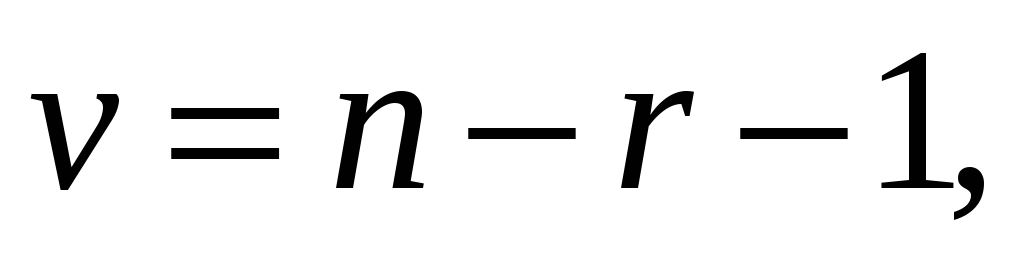где n-число частичных интервалов, r-число параметров распределения F(x),т.е.

5. сравнивают 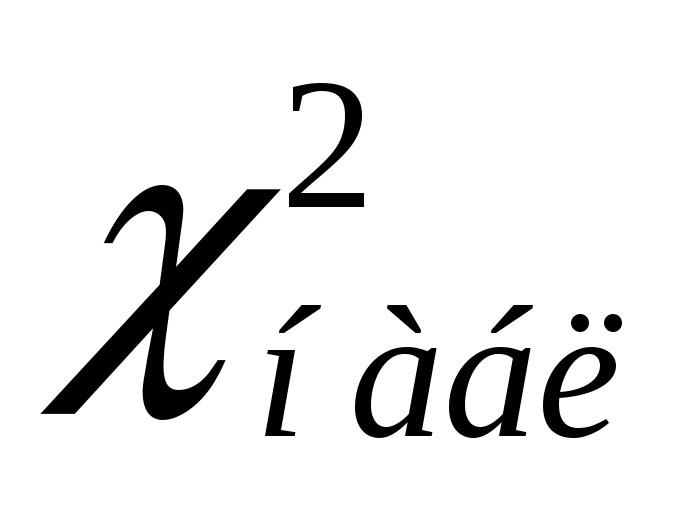и , пользуясь критерием с правосторонней критической областью, т.е. если :

а) , нулевую гипотезу отклоняют;

б) < - нет оснований отвергнуть нулевую гипотезу.

Зам.: При применении критерия важно, чтобы в каждом частичном интервале было не меньше 5 значений или элементов, т.е. , если , то частичные интервалы объединяются.