Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального
образования «Санкт-Петербургский государственный морской технический университет»
(СПбГМТУ)
КОНСПЕКТ ЛЕКЦИЙ ПО ДИСЦИПЛИНЕ МАТЕМАТИКА
Направление подготовки: 180100 «Кораблестроение, океанотехника и системотехника объектов морской инфраструктуры»;
Профили подготовки: 1.180100.62.01 «Кораблестроение», 1.180100.62.03 «Океанотехника».
Квалификация (степень) выпускника: Бакалавр техники и технологии
Форма обучения: очная
Санкт-Петербург
2011
Раздел 5. Дифференциальное исчисление функции нескольких переменных
5.1. Дифференцирование функций нескольких переменных
Начала функционального анализа. Множества точек на плоскости и в пространстве. Окрестности точек. Функция двух переменных и ее геометрическое изображение. Понятие о функции трех и n переменных. Линии и поверхности уровня. Предел и непрерывность функции двух переменных. Свойства функций, непрерывных в замкнутой области. Частные производные, их геометрический и физический смысл. Полное приращение функции двух переменных, дифференцируемость функции двух переменных. Необходимое и достаточное условие дифференцируемости. Полный и частный дифференциалы. Применение полного дифференциала к приближенным вычислениям. Сложная функция нескольких переменных, ее дифференцирование. Инвариантность формы дифференциала. Производные и дифференциалы высших порядков. Неявные функции одной и нескольких переменных. Теорема существования неявной функции. Производные неявных функций. Градиент и производная по направлению. Касательная плоскость и нормаль к поверхности. Геометрический смысл полного дифференциала. Формула Тейлора для функций двух переменных.
5.1.1. Прямое произведение множеств. n – мерное пространство Rn .
Определение 5.1.1
Пусть заданы два множества X и Y . Прямым произведением X ×Y этих множеств называется множество всех упорядоченных пар (x, y), где x X и y Y .
ЗАМЕЧАНИЕ
Упорядоченность пары (x, y) следует понимать в том смысле, что (x, y) ≠ (y, x).
Задача 5.1.1
Если заданы множества X = {1,2,3} и Y = {p, q}, то их прямым произведением является следующее множество
X ×Y = {(1, p); (1, q); (2, p); (2, q); (3, p); (3, q)}.
Задача 5.1.2
Если R – множество всех вещественных чисел, то прямое произведение R × R или
пространство R2 – это множество всех упорядоченных пар вещественных чисел. Если использовать метод координат, то можно установить взаимно однозначное соответствие
между элементами (x, y) R2 и точками M (x, y) плоскости с выбранной на ней системой координат.
Задача 5.1.3
R × R × R или пространство R3 - это множество всех упорядоченных троек вещественных чисел. Метод координат позволяет установить взаимно однозначное
соответствие между элементами (x, y, z) R3 и точками M (x, y, z) трехмерного Евклидова пространства с выбранной в нем декартовой системой координат.
Определение 5.1.2
Прямое произведение R × R ×... × R , то есть множество всех упорядоченных n раз
наборов (x1, x2,..., xn ) из n вещественных чисел называется n – мерным пространством и обозначается: Rn . Элементы (x1, x2,...xn ) Rn называются точками пространства Rn и обозначаются M (x1, x2,..., xn ). Вещественные числа x1, x2,...xn
называются координатами точки M .
2
Определение 5.1.3 |
|
|
|
|
|
|
(x1 |
, x1 ,..., x1 )и M |
|
(x2 |
|
,..., x2 )пространства Rn |
||
Расстоянием между точками M |
1 |
2 |
, x2 |
|||||||||||
|
|
|
|
|
|
1 |
2 |
n |
1 |
2 |
|
n |
||
называется число, ρ(M1, M 2 ), которое определяется по формуле: |
||||||||||||||
ρ(M |
1 |
, M |
2 |
) = |
(x1 − x2 )2 + (x1 |
− x2 )2 |
+ ... + (x1 |
− x2 )2 . |
||||||
|
|
|
1 |
|
1 |
2 |
2 |
|
|
|
n |
n |
||
Теорема 5.1.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Расстояние ρ(M1, M 2 ) |
между |
точками |
M1 |
и |
M 2 |
|
из пространства Rn |
|||||||
удовлетворяет следующим соотношениям:
a)ρ(M1, M 2 ) ≥ 0.
b)ρ(M1, M 2 ) = 0 M1 = M 2 .
c)ρ(M1, M 2 ) = ρ(M 2, M1).
d)ρ(M1, M 2 ) ≤ ρ(M1, M 3)+ ρ(M 3, M 2 ).
Утверждения a, b и c теоремы очевидны из определения расстояния. Утверждение
d , так называемое неравенство треугольников, доказывается аналогично тому, как это было сделано для расстояния в линейном векторном евклидовом пространстве.
Пространство Rn , в котором определено расстояние между двумя точками (метрика),
называется метрическим.
5.1.2. Окрестности точек в пространстве Rn . Классификация точек. Открытые и
замкнутые множества.
Определение 5.1.4 |
|
|
|
|
|
|
|
|
|||||
Пусть M |
0 |
(x0 |
, x0 |
,..., x0 ) Rn |
и δ > 0 – |
вещественное число. δ – окрестностью |
|||||||
|
|
|
1 |
2 |
|
n |
|
|
|
|
|
|
|
точки |
M |
0 |
|
называется |
множество точек |
M (x , x |
2 |
,..., x |
n |
) Rn , для которых |
|||
|
|
|
|
|
|
|
|
1 |
|
|
|||
справедливо: ρ(M0, M ) < δ. δ – окрестность точки M 0 обозначается Uδ(M0 ).
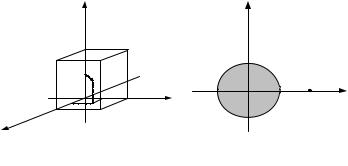
Задача 5.1.4
y |
z |
|
δ |
M0
x x
δ
M0
y
Рис. 5.1.1. Рис. 5.1.2.
Если M 0 R2 , то Uδ(M0 ) – открытый круг (граница не входит в это множество) с
центром в точке M 0 |
и радиусом δ (рис. 5.1.1). Если M 0 R3, то Uδ(M 0 )- открытый |
||||||||||||||||
шар (граница не входит в это множество) |
с центром в точке M 0 и радиусом |
|
δ |
(рис. |
|||||||||||||
5.1.2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение 5.1.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пусть M |
0 |
(x0 |
, x0 |
,..., x0 ) Rn и |
δ > 0 |
. Проколотой δ – окрестностью точки |
M |
0 |
|||||||||
|
1 |
2 |
|
|
n |
|
|
|
|
|
|
|
|
|
|
||
называется множество U |
δ |
(M |
0 |
) \ {M |
0 |
}, то есть множество точек M (x , x |
2 |
,..., x |
n |
) Rn , |
|||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||
3
для которых справедливо: 0 < ρ(M 0, M ) < δ. Проколотая |
δ – окрестность точки M 0 |
||||||
обозначается U&δ(M 0 ). |
|
|
|
|
|
||
Определение 5.1.6 |
|
|
|
|
|
||
Точка |
M 0 |
D R n называется |
внутренней точкой множества |
D , |
если |
||
Uδ(M 0 ) D . |
|
|
|
|
|
||
Определение 5.1.7 |
|
|
|
|
|
||
Точка |
M 0 |
называется |
граничной |
точкой множества |
D Rn , если |
ее |
любая |
окрестность содержит как точки множества D , так и точки, не принадлежащие D . |
|
||||||
Определение 5.1.8 |
|
|
|
|
|
||
Точка |
M0 |
называется |
предельной |
точкой множества |
D Rn , если |
любая ее |
|
проколотая окрестность содержит хотя бы одну точку множества D .
ЗАМЕЧАНИЕ
Граничные и предельные точки множества могут и не принадлежать этому множеству.
Определение 5.1.8
Совокупность всех граничных точек множества называется его границей.
Задача 5.1.5
Для |
множества точек M (x, y, z) пространства R3 , для которых справедливо: |
0 ≤ x ≤ 1 |
|
|
≤ 1, и которое геометрически в прямоугольной системе координат изображается |
0 ≤ y |
|
|
≤ 1 |
0 ≤ z |
|
кубом (рис. 5.1.3), начало координат O(0,0,0) является граничной и предельной точкой, а точка – внутренней и предельной.
Рис. 5.1.3. |
Рис. 5.1.4. |
Задача 5.1.6
Пусть множество D R2 является объединением множества пар чисел (x, y), для которых x2 + y2 <1, и точки M (2,0). Все точки этого множества кроме точки M
внутренние и предельные. Точки (x, y), для которых x2 + y 2 = 1 – граничные и
предельные (рис. 5.1.4). Точка M не является ни внутренней, ни предельной, ни граничной.
Определение 5.1.9
Множество D Rn называется открытым, или связной областью, если все его точки внутренние.
Определение 5.1.10
Множество D Rn называется замкнутым, если оно содержит все свои предельные точки.
4
Задача 5.1.7 |
|
E = {(x, y): x2 + y2 < 1} является открытым. |
|
|
Множество |
E R2 : |
Множество |
||
D R2 : D = {(x, y): x2 + y2 |
≤ 1}является замкнутым. |
|
||
ЗАМЕЧАНИЕ |
|
|
|
|
Не следует |
понимать, |
что |
любое множество открыто или замкнуто. |
Множество |
{(x, y): x2 + y 2 <1} {(2,2)}, согласно определению, не является ни тем, ни другим. Кроме того, можно указать множества, которые и замкнуты и открыты одновременно. Например, множество вещественных чисел R и замкнуто и открыто одновременно. Если его не
рассматривать как подмножество R2 , то оно открыто. Если считать R R2, то оно замкнуто.
5.1.3. Функции n переменных. Предел и непрерывность функции n переменных
Определение 5.1.11
Функцией n переменных называется отображение некоторого множества D Rn во множество вещественных чисел R . Иначе говоря, функция – это правило, по которому
M (x1, x2,..., xn ) Rn ставится в соответствие вещественное число w . Это правило (соответствие) обозначают: w = f (x1, x2,..., xn ) или w = f (M ).
Множество D |
называется |
|
областью определения функции, а множество |
E = {w R : w = f (M ), M D } – областью значений функции w = f (M ). |
|||
ЗАМЕЧАНИЕ |
|
|
|
Если D R2 , то |
w = f (x , x |
2 |
) - функция двух переменных. Обычно для функции двух |
|
1 |
|
|
переменных используют обозначение z = f (x, y).
В трехмерном евклидовом пространстве с введенной декартовой системой координат функция z = f (x, y) задает некоторую поверхность. Например, функция
задает параболоид вращения (рис. 5.1.5).
z 
y
x
Рис. 5.15.
Задача 5.1.8
Найдите область определения и область значений функции двух переменных z = 
4 − x2 − y2 .
Решение
Область определения заданной функции находится из условия 4 − x2 − y2 ≥ 0, или x2 + y2 ≤ 4. Из последнего неравенства следует, что область определения D R2 –
это внутренность круга, ограниченного окружностью x2 + y2 = 4.
5