2.3. Расчет рам методом сил

В методе сил в качестве основной выбирается обычно статиче­ски определимая система, получаемая из заданной n раз статически неопределимой системы путем отбрасывания n жестких связей или постановкой (введением) шарниров. Этими жесткими связями мо­гут быть жесткие опоры или связи, соединяющие одну часть стерж­ня с другой. Усилия взамен отброшенных связей прикладываются в месте разреза или введенного шарнира в виде поперечных, про­дольных сил или изгибающих моментов.

Можно выбрать различные варианты основной системы. Необ­ходимо, чтобы полученные таким образом основные системы были статически определимыми и кинематичеcки неизменяемыми.

Раccмотpим в качестве примера трижды статически неопреде­лимую систему (рис. 2.6, а). Разpезав опоpные cтеpжни опоpы A и C и заменяя их влияние cилами X₁, X₂, X₃, полyчим один из воз­можных ваpиантов оcновной cиcтемы (pиc. 2.6, б). Втоpой ваpиант полyчим пyтем pазpеза в жеcткой заделке В, и замены его влияния введением cил X₁, X₂ и момента X₃  (pиc. 2.6, в). Тpетий вариант получаем введением в узел D шарнира, удалением из узла C жест­кой опоры и введением в узел В шаpниpно-неподвижной опоры взамен жесткой заделки (рис. 2.6, г).

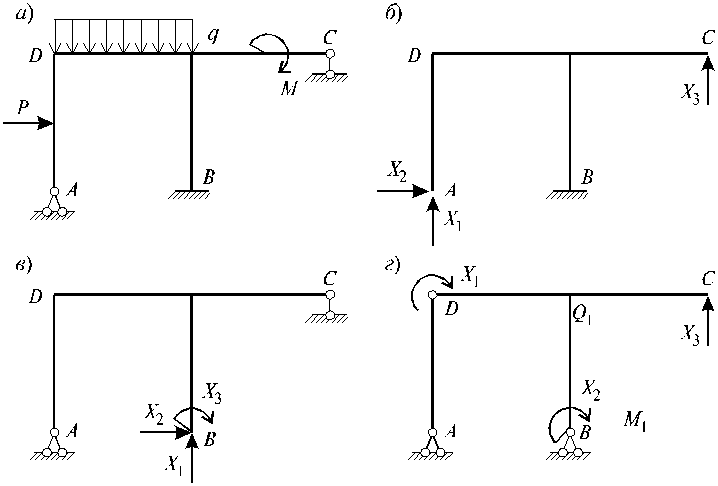
Рис. 2.6

Все полученные системы являются статически определимыми и геометрически неизменяемыми, поэтому они могут быть исполь­зованы для расчета. Однако из них надо выбрать наиболее простую для расчета. Веpоятно, наиболее простым является I-ый вариант (рис. 2.6, б), так как консольная система, как правило, проще рас­считывается (нет необходимости находить опорные реакции).

Для основных систем неконсольного вида необходимо в первую очередь вычислить, пользуясь уравнениями равновесия, опорные реакции, а затем, приняв их за внешние силы, построить эпюры. Для избежания ошибок всегда следует проводить проверку пра­вильности вычисления опорных реакций.

Поcле выбора основной системы составляют дополнительные уравнения совместности деформаций, называемые каноническими уравнениями метода сил. Количество их всегда равно числу неиз­вестных усилий.

Каноничеcкие уравнения метода сил составляются для основной системы из условия равенства нулю перемещений по на­правлению внешних лишних связей и относительных перемещений по направлению внутренних лишних cвязей. Итак, в основной сис­теме перемещения по направлению каждого из неизвестных усилий X_i (i = 1, 2, 3,..., n) от всех действующих на нее силовых факторов должны быть равны 0, т.е.

D_iР + d_i1 X₁ + d_i2 X₂ +...+ d_in X_n = 0,    (i = 1, 2, 3,..., n), (2.6)

где D_iР - перемещение в основной системе по направлению отбро­шенной i-ой связи от действия внешних нагрузок; d_in - перемещение в основной системе по направлению отброшенной i-ой связи от дей­ствия единичного усилия X_k = 1 (k = 1, 2, 3,..., n).

Из теоремы о взаимности перемещений, примененной к основ­ной системе, следует, что d_ik = d_ki .

Очевидно, что выполнения равенства (2.6) является необходимым и достаточным условием эквивалентности заданной и основной систем. Система (2.6) называется каноническим уравнением метода сил.

Решив систему уравнений (2.6) относительно X_i , мы можем за­менить дальнейший расчет заданной статически неопределимой си­стемы расчетом статически определимой основной системы, нагру­женной той же нагрузкой с дополнением усилий X₁, X₂,..., X_n , заменяющих влияние отброшенных связей.

Для определения коэффициентов d_ik и свободных членов D_iР канонических уравнений (2.6) в методе сил применяют формулу Мора (2.3) или для рам уравнение (2.5), выражающее перемещения через внутренние силы в стержневой системе.

При вычислении коэффициентов и свободных членов канони­ческих уравнений метода сил, кроме непосредственного интегриро­вания (2.5) применяют различные упрощенные приемы вычисле­ния интегралов. Особенно обстоятельно они разработаны для рам с прямолинейными стержнями постоянного сечения. Жесткость EJ = = const при этом выносится за знак интеграла, а под интегралом остается произведение двух функций: M_i и M_k , одна из которых, как правило, или обе являются линейными функциями. Операция интегрирования здесь часто называется перемножением эпюр и ее символически изображают следующим образом:

, (2.7)

здесь знак означает умножение в смысле формулы Мора.

Применение готовых формул показано в таблице 2.1. Сами эти формулы без труда определяются элементарными методами. Эта таблица является весьма универсальной, так как она пригодна для определения перемещений по двум любым прямолинейным эпю­рам, а также криволинейной с прямолинейной. Если любая из фи­гур, приведенных в табл. 2.1, перемножается с треугольником, то это перемножение сводится к трапеции, одна из ординат которых равна 0. При перемножении на прямоугольник нужно учесть, что М_a = М_b .

При помощи расчленения эпюр на части можно добиться того, чтобы при перемножении участвовали эпюры простой структуры, приведенные в табл. 2.1.

Например, пусть нужно перемножить эпюры, приведенные на рис. 2.7. Каждую из эпюр можно представить в виде суммы: в пер­вом случае, в виде двух треугольных и параболической; во втором -в виде двух треугольных.

Рис. 2.7 Рис. 2.8

Итак, .

Тогда

.

А далее следует воспользоваться формулой для вычисления ин­тегралов , приведенных в табл. 2.1.

Довольно удобным способом перемножения эпюр является способ Верещагина. Этот способ применим в случае когда из двух перемножаемых эпюр одна как минимум является прямоли­нейной. Если одна из эпюр является криволинейной вычисляется площадь W криволинейной эпюры, которая умножается на ордина­ту под ее центром тяжести, взятую в прямолинейной эпюре (рис. 2.8).

Предположим M₁ = f (x); M₂ = a x + b, тогда

=

=,

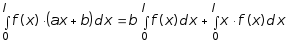но величина =W представляет собой площадь криволи­нейной эпюры, а величина = S - статический момент площади этой эпюры относительно левого конца стержня. Следо­вательно,

.

Известно, что величина S/W представляет собой ординату центра тяжести криволинейной эпюры, а b + a×S/W - значение M₂ при x_с = S/W.

В случае двух криволинейных эпюр способ Верещагина непри­меним. Надо пользоваться интегралом Мора. Способ Верещагина применим также в тех случаях, когда одна  из эпюр не криволиней­ная, а ломаная.

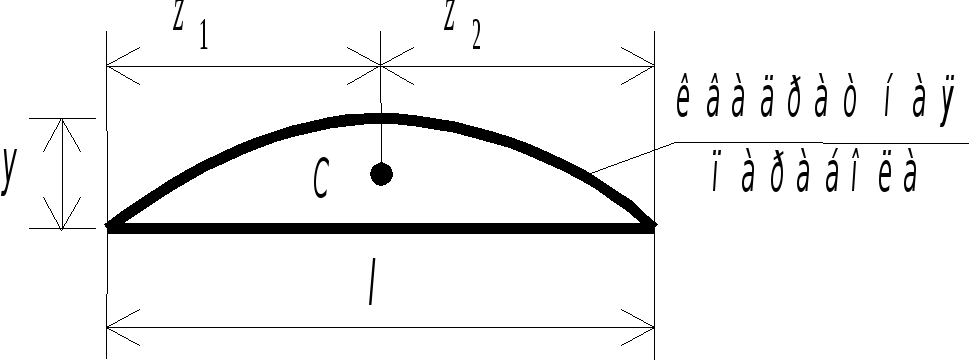
В таблице 2.2 приведены формулы для определения площади W, положения центра тяжести z_C и ординаты y_C в центре тяжести для некоторых довольно распространенных плоских фигур.

В случае, когда имеются эпюры общего вида (например, обе эпюры криволинейные, либо трапеции, рис. 2.8), разбиение уже на два равных интервала дает согласно формуле Симпсона точное выражение интеграла:

,

где индексы А и С относятся к сечениям расположенным на концевых сечениях интервала длиной l, а индекс В к серединному сечению того же интервала.

В тех случаях, когда функции M₁ и M₂ в рассматриваемом интервале длиной l, являются линейными и известны их значения в концевых сечениях интервала, то формулу переумножения M₁ и M₂ можно преобразовать в следующем виде:

. (2.8)

Итак, после составления и решения канонической системы уравнений метода сил (2.6) мы получаем значения X₁, X₂, X₃,..., X_n , т.е. значения усилий в лишних связях. Затем строим для основной системы эпюры изгибающих моментов от каждого из найденных усилий. Для этого могут быть использованы построенные ранее единичные эпюры, все ординаты которых необходимо теперь умно­жить на найденные значения соответствующих неизвестных.

Таблица 2.2

№№	Фигура	Площадь	Абсциссы центра тяжести
n/n			z1	z2
1.		y l
2.
3.
4.
5.

Сложив по характерным сечениям (на протяжении всей рас­считываемой конструкции) ординаты эпюр от действия всех сил X_i с ординатами грузовой эпюры, получим окончательную (суммар­ную) эпюру изгибающих моментов в заданной статически неопре­делимой системе.