5. Мокрая очистка газов

Очистку газов от частичек пыли и капелек тумана путем контакта газа с жидкостью используют в тех случаях, когда подлежащие очистке газовые потоки не имеют высокой температуры, при которой происходило бы значительное испарение или даже кипение жидкости.

Поверхностью контакта между газом и жидкостью может быть суммарная поверхность жидкой пленки, стекающей по слою твердой насадки типа керамических колец Рашига, или поверхность газовых пузырей в жидкости.

Основное требование к жидкости, используемой для мокрой очистки газов от пыли, – ее способность смачивать поверхность частиц, которые эта жидкость должна улавливать.

Конструкции аппаратов для мокрой газоочистки различны. Полые распылительные скрубберы (уловители) представляют собой вертикальные аппараты круглого сечения, в которых очищаемый запыленный газ может подаваться как сверху, так и снизу, а жидкость разбрызгивается в верхней части аппарата. Частицы пыли (или тумана) захватываются поверхностью падающих капелек, и так называемый шлам, т. е. жидкость с уловленными ею частицами, выводится из нижней части аппарата.

В насадочных скрубберах внутренний объем вертикальной колонны заполнен инертной насадкой, по поверхности которой стекает пленка подаваемой сверху жидкости. Газовый поток проходит в зазорах между элементами насадки, при этом частицы пыли из газа захватываются пленкой жидкости и в нижней части скруббера вместе с жидкостью выводятся из аппарата.

Центробежные пленочные скрубберы, по существу, представляют собой циклоны (см. рис. 13), на внутреннюю поверхность корпуса которых сверху в виде пленки подается жидкость. Как и в обычном циклоне, центробежная сила отбрасывает частицы к стенке корпуса, где они поглощаются пленкой жидкости. При этом уменьшается опасность вторичного захвата пыли уже очищенным газовым потоком (см. центробежную очистку газов).

Барботажные (пенные) пылеуловители (рис. 23) используются для очистки газов с повышенным содержанием пыли. Запыленный газ (Г + Т) поступает под газораспределительную решетку 2, на которую подается жидкость (Ж). Запыленный газ барботирует через слой 3 жидкости и далее проходит через слой 4 образующейся пены. Частицы пыли захватываются поверхностью жидкости и отводятся в виде шлама (Ш) через сливной порог 5 и частично – с протечками через отверстия решетки.

Пенные пылеуловители обладают сравнительно высокой улавливающей способностью даже для весьма мелких частиц (частицы размером 5 мкм

Р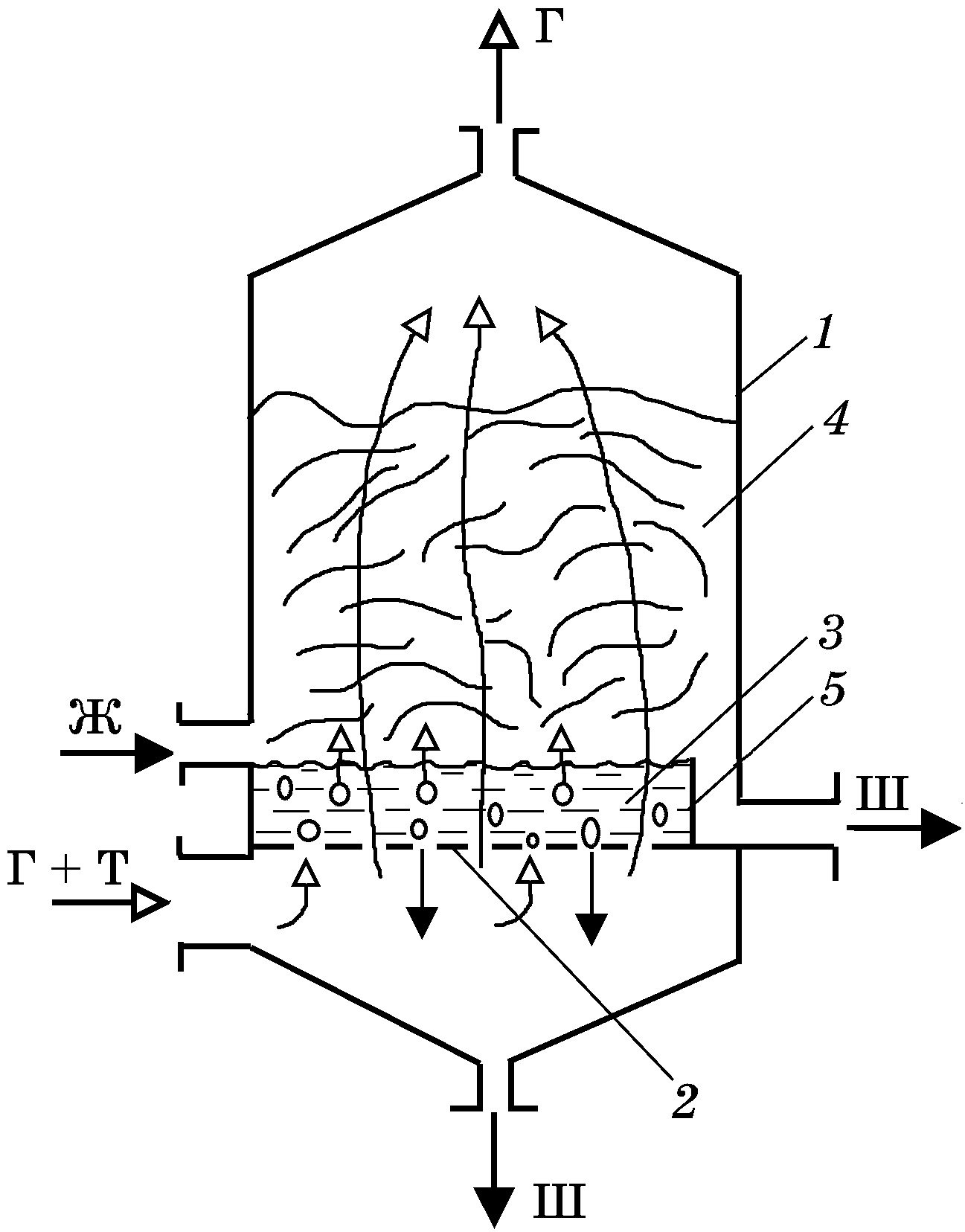ис. 23. Барботажный (пенный) пылеуловитель:

1 – корпус; 2 – газораспределительная решетка; 3 – слой жидкости; 4 – слой пены; 5 – переливной порог; Г + Т – запыленный газ; Ж – жидкость; Г – очищенный газ; Ш – шлам

улавливаются на 80–90 %), но отклонение скорости подаваемогопод решеткугаза от расчетного значения (3м/с) может приводить либо к большому уносу пеныгазовым потоком, либо, наоборот, – к проливу жидкости через отверстия решетки.

В заключение отметим, что выбор того или иного метода гидромеханического разделениянеоднородных сред зависит от многих факторов: от требуемой эффективности разделения, исходной концентрации дисперсной фазы, среднего размера частиц истепени неоднородности частиц по их размерам, температуры поступающего на разделение гетерогенного потока, его химической агрессивности и т. п. В зависимости от преимуществ и недостатков каждого из способов разделения и по результатам технико-экономического анализа, т. е. определения капитальных, эксплуатационных и приведенных затратпроизводится выбор того или иного способа разделения и размеров основных аппаратов.

Вопросы для самопроверки

1.	Как классифицируются методы разделения неоднородных систем?
2.	От каких сил зависит скорость гравитационного осаждения частиц?
3.	Запишите уравнение скорости периодической фильтрации.
4.	На основе каких экспериментальных данных определяются константы скорости фильтрации?
5.	Каковы основные конструкции фильтров периодического и непрерывного действия?
6.	Какие силы действуют на частицы при центробежном разделении?
7.	Что такое фактор разделения центрифуг?
8.	Какие существуют способы выгрузки осадков из фильтрующих и осадительных центрифуг?
9.	Какие силы действуют на частицы при электроочистке запыленных газов?
10.	Поясните принцип действия и перечислите основные виды мокрой очистки запыленных газов.

ПРИМЕРЫ

Осаждение

Пример 1. Определить скорость осаждения сферических частиц диаметром 0,10 мм из материала плотностью 2400 кг/м³ при температуре 20 °С: а) в воздухе при атмосферном давлении; б) в воде.

Решение. Поскольку размер осаждающихся частиц невелик, то имеет смысл вначале использовать формулу (1) для ламинарного обтекания сферы.

а) В воздухе

w_ос = (2400 – 1,21) 9,81 (0,10  10^–3)²/(l8  0,0185  10^–3) = 0,710 м/с,

где  = (29/22,4) (273/293) = 1,21 кг/м³ и  = 0,0185  10^–3 Па  с – плотность и вязкость воздуха при 20 °С.

Значение критерия Рейнольдса

Re_ос = 0,710  0,1  10^–3  1,21/(0,0185  10^–3) = 4,65.

Поскольку Re_oc = 4,65 > 0,2, то режим обтекания сферической частицы не соответствует ламинарному и использование формулы Стокса (1) не является правомерным.

Согласно универсальному методу расчета скорости осаждения следует вычислить значение критерия Архимеда по формуле (3):

Аr = (2400 – 1,21) 1,21  9,81 (0,1  10^–3)³/(0,0185  10^–3)² = 83,3.

По графику для сферических частиц (рис.1) находится значение Re_oc = 3,2, откуда

w_oc = 3,2  0,0185  10^–3/(0,1  10^–3  1,21) = 0,489 м/с.

Таким образом, неправомерное использование формулы ламинарного обтекания Стокса в данном случае приводит к завышению скорости осаждения почти в два раза (0,710 м/с против правильного значения 0,489 м/с).

б) В воде

w_ос= (2400 – 998) 9,81 (0,10  10^–3)²/(18  1,005  10^–3) = 0,0076 м/с,

где  = 998 кг/м³ и  = 1,005  10^–3 Па  с – плотность и вязкость воды при 20 °С.

Критерий Рейнольдса при осаждении в воде

Re_oc = 0,0076  0,1  10^–3  998/(1,005  10^–3) = 0,758.

Поскольку и здесь Re_oc > 0,2, то обтекание частицы и здесь не ламинарное, поэтому скорость осаждения рассчитывается универсальным способом, для чего вычисляется значение критерия Архимеда

Аr = (2400 – 998) 998  9,81 (0,1  10^–3)³/(1,005  10^–3)² = 13,9.

По графику на рис. 1 находится значение Re_ос = 0,7, откуда

w_oc = 0,7  1,005  10^–3/(0,1  10^–3  998) = 0,00705 м/с.

Можно произвести проверочный расчет, определив из рис. 2.1 значение критерия Лященко: Ly = 0,02, откуда

w_ос = (0,02 [1,005  10^–3(2400 – 998) 9,81]/998²)^1/3 = 0,0652 м/с.

Разность полученных значений лежит в пределах точности отсчетов по рис. 1.

Пример 2. Определить эквивалентные диаметры продолговатых частиц каменного угля и плоских частиц сланца (_сл = = 2200 кг/м³), осаждающихся с одинаковой скоростью w_ос = = 0,10 м/с в воде при 20 °С.

Решение. Вычисляются значения критериев Ly согласно формуле (2):

для частиц угля

Ly_y = 0,10³  998²/[1,005  10^–3 (1350 – 998) 9,81] = 287,

для частиц сланца

Ly_сл = 0,10³  998²/[1,005  10^–3 (2200 – 998) 9,81] = 84,0,

где  = 998 кг/м³ и  = 1,005  10^–3 Па  с – плотность и вязкость воды при 20 °С; _у = 1350 кг/м³ – плотность каменного угля .

По графику рис. 1 определяются соответствующие значения критерия Архимеда:

для продолговатых частиц угля Ar_y = 9  10⁴, откуда согласно формуле (3):

d_{э, у} = = 2,82 10^–3 м;

для пластинчатых частиц сланца Аr_сл = 7  10⁴, откуда

d_э, сл = = 1,81  10^–3 м.

Пример 3. Каково должно быть расстояние между горизонтальными полками пылеосадительной камеры (рис. 2), чтобы успевали осаждаться частицы колчеданной пыли диаметром 8,0  10^–6 мм из потока печного газа, расход которого составляет 0,60 м³/с (при нормальных условиях), температура 427 °С, вязкость 0,034  10^–3 Па  с и плотность 0,50 кг/м³. Плотность колчедана 4000 кг/м³. Размеры рабочего объема камеры: длина 4,1 м, ширина 2,8 м и общая высота 4,2 м.

Решение. Объемный расход газа пересчитывается на заданную температуру:

V_c = 0,60 (273 + 427)/273 = 1,54 м³/с.

Линейная скорость движения газа вдоль полок камеры

w_г = 1,54/(2,8  4,2) = 0,131 м/с.

Время пребывания газа в камере

^– = L/w_г = 4,1/0,131 = 31,3 с.

Скорость осаждения одиночной сферической частицы находится по формуле Стокса (1):

w_ос = (4000 – 0,50) 9,81 (8  10^–6)²/(18  0,034  10^–3) = 0,0041 м/с.

Производится проверка правильности применения формулы (1), для чего находится значение критерия Рейнольдса

Re_oc = 0,0041  8  10^–6  0,50/(0,034  10^–3) = 0,000482 < 0,2.

Для расчета пылеосадительной камеры действительная скорость осаждения частиц принимается в два раза меньшей: 0,00410/2 = = 0,00205 м/с.

Искомое расстояние между соседними горизонтальными полками определяется как путь, проходимый осаждающимися частицами в течение времени их пребывания в рабочей зоне камеры:

h = w_ос^– = 0,00205  31,3 = 0,0642 м.

Пример 4. Определить диаметр отстойника (рис. 3) для непрерывного осаждения частиц мела в воде при 15 °С. Производительность отстойника 80 т/ч начальной суспензии, массовая доля мела в которой 8 %. Диаметр наименьших частиц, подлежащих осаждению, составляет 0,035 мм. Влажность образующегося шлама 70 %.

Решение. Находится скорость осаждения частиц при ламинарном режиме обтекания (формула (1)):

w_ос = (2200 – 1000) 9,81 (0,035  10^–3)²/(18  1,14  10^–3) = 0,000703 м/с,

где _ч = 2200 кг/м³ – плотность мела;  = 1,14  10^–3 Па  с – вязкость воды при 15 °С.

Проверка значения критерия Рейнольдса

Re_oc = 0,000703  0,035  10^–3  1000/(1,14  10^–3) = 0,0216 < 0,2.

Действительная скорость осаждения частиц в реальном аппарате

w_oc = 0,000703/2 = 0,000351 м/с.

Площадь отстойника определяется по формуле (5)

S_ос = (80  10³/3600) (1 – 8/30)/(1000  0,000351) = 46,4 м².

Диаметр отстойника

D = = = 7,69 м.

Пример 5. Определить необходимую высоту отстойника (рис. 2.3), если для уплотнения водной суспензии в зоне ее cгyще­ния необходимо 16 часов. Относительная плотность частиц равна 2,6. Среднее разбавление в зоне сгущения Т : Ж = 1 : 1,5. Суточная производительность отстойника диаметром 10 м составляет 23 т по твердой фазе.

Решение. По формуле (11) определяется плотность суспензии в зоне сгущения

Массовая доля твердой фазы в суспензии в зоне сгущения, согласно определению, х = 1/(1 + 1,5) = 0,40 кг тв./кг сусп. Следовательно, 1 м³ сгущенной суспензии содержит массу твердой фазы T = _cx = 1330  0,40 = 531 кг.

В течение суток на 1 м² осаждается масса твердой фазы 23/(0,785  10²) = 0,293 т/(м²  сут).

Через зону сгущения за 16 ч пройдет 0,293(16/24) = 0,195 т твердой фазы на 1 м² площади осаждения.

Поскольку в зоне сгущения 1 м³ суспензии содержит 0,531 кг твердой фазы, то высота этой зоны

h₂ = 0,195/0,531 = 0,368 м.

По практическим данным высота зоны питания принимается из диапазона 0,45–0,75 м, т. е. можно принять h₁ = 0,60 м.

Высота нижней зоны, в которой вращаются скребки, зависит от наклона лопастей, и ее согласно практическим данным можно принимать соответствующей 0,15 м на 1 м радиуса отстойника. Следовательно, h₃ = 0,15(10/2) = 0,75 мм.

Суммарная высота отстойника

H = h₁ + h₂ + h₃ = 0,60 + 0,368 + 0,75 = 1,72 м.

Пример 6. Вычислить время, необходимое для получения 30 л фильтрата из суспензии через 2,5 м² поверхности фильтрующей перегородки, если при предварительном испытании той же суспензии при тех же фильтрующей перегородке и разности давлений с 1,2 дм² опытного фильтра было собрано: 0,025 л фильтрата через 2,3 мин и 0,080 л через 15 мин после начала фильтрования.

Решение. Имеющиеся опытные данные используются для подстановки в уравнение фильтрования (7) и определения констант фильтрования:

(0,025  10^–3/1,2  10^–2)² + 2 (0,025  10^–3/1,2  10^–2) С = K (2,3  60),

(0,080  10^–3/1,2  10^–2)² + 2 (0,080  10^–3/1,2  10^–2) С = K (15  60),

откуда K = 5,52  10^–8 м²/с и С = 0,785  10^–3 м.

Полученные значения K и С используются для вычисления времени фильтрования:

(30  10^–3/2,5)² + 2 (30  10^–3/2,5) 0,785  10^–3= 5,52  10^–8 ,

откуда  = 3,16  10³ с = 52,7 мин.

Пример 7. С помощью барабанного вакуум-фильтра (рис. 2.4) непрерывного действия необходимо фильтровать 2,36  10^–3 м³/с водной суспензии, содержащей 17,6 % мелкодисперсной твердой фазы и имеющей плотность _с = 1120 кг/м³. Влажность получаемого осадка должна быть 34 % при разрежении внутри барабана 600 мм рт. ст. В процессе фильтрования на лабораторной модели при разрежении 510 мм рт. ст. были получены следующие значения констант фильтрования: K = 11,2  10^–6 м²/с, C = 6,0  10^–3 м³/м², а влажность осадка 34 % достигнута за 32 с. Определить требуемые поверхность фильтрования и частоту вращения барабана.

Решение. Приближенно принимая значения константы K при прочих равных условиях пропорциональными разности давлений по обе стороны от фильтрующей перегородки (см. формулу (6)), для рабочего разрежения 600 мм рт. ст. пересчитывается новое значение константы фильтрования:

K/11,2  10^–6 = 600/510, откуда K = 13,1  10^–6 м²/с.

Производительность 1 м² фильтрующей перегородки за время 32 с находится из уравнения (2.7):

V = – 6,0  10^–3 += 15,3  10^–3 м³/м².

Удельная производительность 1 м² фильтрующей перегородки, отнесенная к единице времени:

v_ф = 15,3  10^–3/32 = 0,479  10^–3 м³/(м²  с).

Заданная производительность по суспензии пересчитывается на производительность по фильтрату, для чего предварительно определяется соотношение масс влажного и сухого осадков в конце процесса фильтрования т = 1/(1 – 0,34) = 1,52; при массовой доле твердой фазы в исходной суспензии х = 0,176 массовый ее расход G_c = V_c_c = 2,36  10^–3  1120 = 2,64 кг/с; масса влажного осадка G_ос = G_cхm = 2,64  0,176  1,52 = 0,706 кг/с; масса фильтрата G_ф = G_с – G_ос = 2,64 – 0,706 = 1,94 кг/с. При плотности фильтрата _ф = 1000 кг/м³ его объемный расход составит V_ф = G_ф/_ф = = 1,94/1000 = 1,94  10^–3 м³/с.

Следовательно, необходимая поверхность фильтрования составит

S_ф = V_ф/v_ф = 1,94  10^–3/0,479  10^–3 = 4,05 м².

В барабанных вакуум-фильтрах поверхность зоны фильтрования, погруженной в суспензию, составляет обычно приблизительно 35 % от общей поверхности барабана, следовательно, необходимая общая площадь поверхности:

S = S_ф/0,35 = 4,05/0,35 = 11,6 м².

По каталогу на барабанные вакуум-фильтры ближайший вариант имеет общую поверхность 12 м², диаметр и длину барабана 2,1 м и 1,8 м соответственно.

Частота вращения барабана, обеспечивающая заданное время фильтрования:

n = 0,35/32 = 0,0109 c^–1 =0,656 мин^–1.

Пример 8. Определить необходимый диаметр стандартного циклона для улавливания частиц с наименьшим диаметром 80 мкм из потока воздуха, расход которого V_с = 2000 кг/ч, температура 100 °С; давление атмосферное.

Решение. Предварительное значение условной скорости газа w_ц в цилиндрической части циклона ЦН-15 вычисляется по формуле (14):

w_ц = = = 3,04 м/с,

где значения (р/) = 740 м²/с² и ₀ = 160 принимаются согласно рекомендациям.

Плотность воздуха при 100 °С и атмосферном давлении

 = (29/22,4) 273/(273 + 100) = 0,948 кг/м³.

Диаметр циклона находится из уравнения расхода (13):

D == 0,496 м.

Принимается диаметр циклона D = 0,50 м.

Условная скорость воздуха в циклоне увеличенного диаметра w_ц = 3,04 (0,496/0,50)² = 2,99 м/с, а перепад гидростатического давления р = 160  0,948  2,99²/2 = 679 Па = 69 мм вод. ст.

Пример 9. Определить производительность (по питанию) автоматической осадительной центрифуги АОГ-800 при работе ее на водной суспензии гидроксида магния. Плотность частиц 2525 кг/м³. Температура суспензии 30 °С. Наименьший диаметр частиц 3 мкм. Диаметр барабана центрифуги 800 мм, длина барабана 400 мм, диаметр сливного борта 570 мм, частота вращения барабана 1200 мин^–1. Цикл работы центрифуги составляет 20 мин; из них 18 мин – подача суспензии с одновременным осаждением и 2 мин – разгрузка осадка.

Решение. Часовая производительность центрифуги определяется по формуле (20), для чего предварительно по формуле (1) находится скорость осаждения частиц наименьшего диаметра в поле силы тяжести (в предположении о ламинарном режиме осаждения):

w_ос = (2525 – 1000) 9,81 (3  10^–6)²/(18  0,80  10^–3) = 0,00935  10^–3 м/с,

где  = 0,80  10^–3 Па  с – динамическая вязкость воды при 30 °С.

Скорость осаждения w_ос в поле центробежной силы

w_ос = w_ос [²R/g] = 0,00935  10^–3 [(2  1200/60)² (0,800/2 + 0,570/2)/2/9,8l] =

= 5,29  10^–3 м/с,

где при вычислении фактора разделения центрифуги использован средний радиус кольца суспензии.

Проверяется режим осаждения в поле центробежной силы:

Re = w_осd/ = 5,29  10^–3  3  10^–6  1000/(0,80  10^–3) = 19,8  10^–3 < 0,2.

Отношение периода осаждения к продолжительности общего цикла работы

k = 18/20 = 0,90.

Часовая производительность центрифуги согласно (2.20) при  = 0,45:

V_ч = 25,3  0,45  0,40  1200²  0,343²  0,00935  10^–3  0,90 = 6,49 м³/ч.

Пример 10. Определить значения критической скорости начала псевдоожижения, а также рабочую (на полное сечение аппарата) и действительную (в свободном сечении между частицами) скорости воздуха при числе псевдоожижения K_w = w/w_кр = 1,6 для псевдоожиженного (взвешенного) слоя сферических частиц силикагеля плотностью 1100 кг/м³. Температура воздуха 150 °С. Ситовой состав силикагеля:

Фракция, мм	–2,0 + 1,5	–1,5 + 1,0	–1,0 + 0,5	–0,5 + 0,25
Массовая доля, %	43	28	17	12

Решение. Определение значения критерия Архимеда требует вычисления эквивалентного диаметра частиц, что можно сделать по соотношению d_э = :

d_э = 1/(0,43/1,75 + 0,28/1,25 + 0,17/0,75 + 0,12/0,375) = 0,983 мм,

где d₁ = (2,0 + 1,5)/2 = 1,75 мм, d₂ = (1,5 + 1,0)/2 = 1,25 мм, d₃ = (1,0 + + 0,5)/2 = 0,75 мм и d₄ = (0,5 + 0,25)/2 = 0,375 мм.

Значение критерия Архимеда:

Аr = (1100 – 0,833) 0,833  9,81 (0,983  10^–3)³/(0,024  10^–3)² = 1,47  10⁴,

где плотность воздуха при 150 °С  = 1,29  273/(273 + 150) = 0,833 кг/м³ и  = 0,024  10^–3 Па  с – вязкость воздуха при 150 °С .

По рис. 12 полученному значению Ar = 1,47  10⁴ соответствует значение критерия Ly_кр = 2,5  10^–2 при порозности неподвижного слоя ₀ = 0,4. Откуда скорость начала псевдоожижения

w_кр = =

= =0,210 м/с.

Рабочая скорость воздуха

w = K_ww_кр = 1,6  0,210 = 0,337 м/с.

Порозность взвешенного слоя находится по рис. 2.12 при Ly = = Ly_кр  K³_w = 2,5  10^–2  1,6³ = 0,102 и Аr = 1,47  10⁴, что дает значение 0,48.

Действительная скорость воздуха в зазорах между частицами

w_д = w/ = 0,337/0,48 = 0,702 м/с.

Пример 11. В условиях предыдущего примера определить размеры аппарата и перепад статического давления при прохождении воздуха через него. Через аппарат с псевдоожиженным слоем непрерывно проходит 2,50 т/ч силикагеля при среднем времени его пребывания в слое 10 мин. Расход воздуха при рабочих условиях составляет 4300 м³/ч. Свободное сечение газораспределительной решетки 1,5 % при диаметре отверстий 0,80 мм; толщина решетки 2,0 мм. Плотность неподвижного слоя силикагеля _нас = 650 кг/м³.

Решение. Диаметр цилиндрического аппарата определяется из уравнения расхода при найденной в предыдущем примере скорости воздуха на полное сечение аппарата:

Масса силикагеля в слое находится как произведение массового расхода силикагеля на среднее время пребывания его в слое (соотношение (35)):

М = (2,5  10³/3600) (10  60) = 417 кг.

Объем и высота неподвижного слоя силикагеля

V = М/_нас = 417/650 = 0,642 м³

и

h₀ = V/(/4  D²) = 0,642/(/4  2,12²) = 0,182 м.

Порозность неподвижного слоя

₀ = 1 – _нас/ = 1 – 650/1100 = 0,409.

Высота взвешенного при K_w = 1,6 слоя согласно соотношению (33)

Перепад давления на слое согласно соотношению (29)

р_сл = (1100 – 0,833) 9,81 (1 – 0,48) 0,207 = 1160 Н/м².

Скорость воздуха в отверстиях решетки

w₀ = 0,337/0,015 = 22,5 м/с.

При отношении диаметра отверстия решетки к ее толщине d₀/ = 0,80/2,0 = 0,40 согласно рис. 11 коэффициент  = = 0,63. Тогда перепад давления на решетке согласно формуле (2.30)

р_р = 0,503  0,833  22,5²(1 – 0,015²)/0,63² = 534 Н/м².

Суммарное сопротивление аппарата

р_сл = 1160 + 534 = 1690 Н/м² = 173 мм вод. ст.

П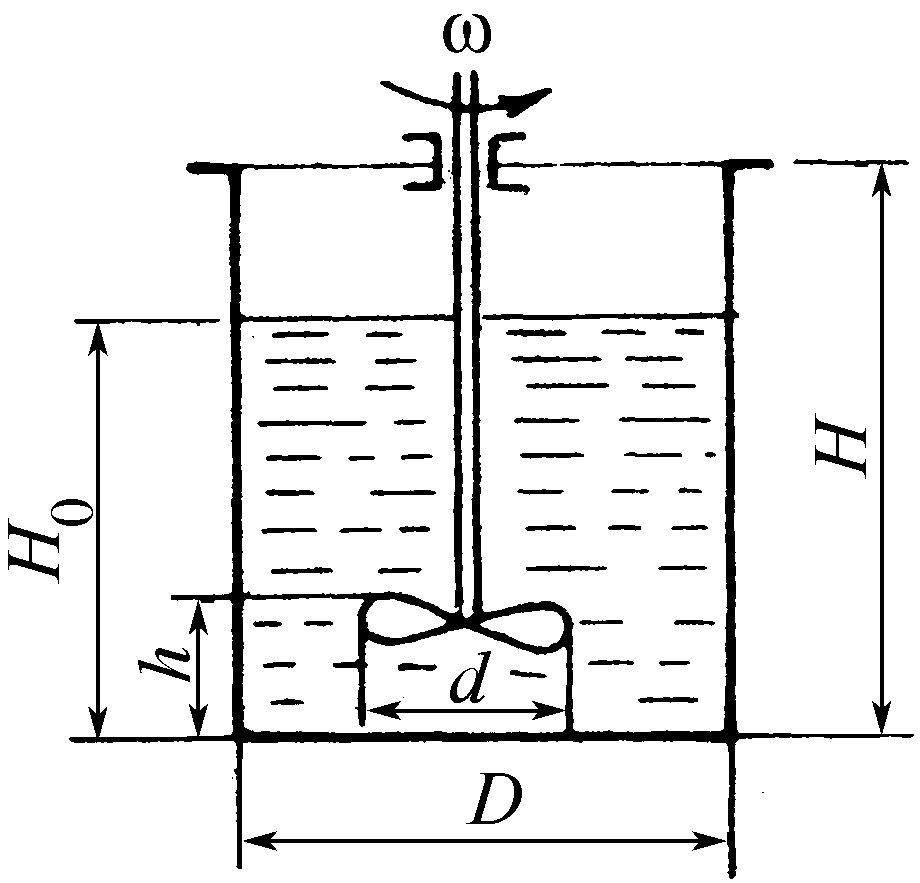ример 12.В аппарате цилиндрической формы диаметром 1200 мм перемешивается жидкая смесь, имеющая плотность 1600 кг/м³ и динамическую вязкость 20  10^–3 Па  с (рис. 2.14). Пропеллерная мешалка вращается с частотой 3,5 с^–1. Определить установочную мощность электродвигателя.

Решение. Диаметр нормализованной мешалки принимается равным одной третьей части диаметра аппарата, не имею­щего поперечных перегородок:

d = D/3 = 1,200/3 = 0,400 м.

Рис. 24. Схема установки перемешивающего устройства в цилиндрическом аппарате

Определяется значение центробежного критерия Рейнольдса

Re_ц = 1600  3,5  0,400²/(20  10^–3) = 44 800.

Полученное значение Re_ц > 60 соответствует турбулентному режиму работы мешалки.

Значение критерия мощности определяется по графику:

K_n = 0,27.

Находится мощность, потребляемая непосредственно мешалкой при работе ее в установившемся режиме:

n = K_Nn³d⁵ = 0,27  1600  3,5³  0,400⁵ = 190 Вт.

Мощность в пусковой период работы мешалки обычно в 2–3 раза превышает мощность в установившемся режиме:

N_пуск = 2,5  190 = 475 Вт.

Установочная мощность электродвигателя, имеющего вместе с механической передачей КПД 0,95 и с учетом 20 % запаса мощности

N_уст = 475  1,20/0,95 = 600 Вт.

КОНТРОЛЬНЫЕ ЗАДАНИЯ

Вариант задания определяется по последней цифре зачетки.

1. Определить скорость осаждения шарообразных частиц плотностью ρ кг/м³ и диаметром d мкм: а) в воде при 15 °С; б) в воздухе при 15 и 500 °С.

№ варианта	ρ , кг/м3	d, мкм
0	3200	5
1	2900	10
2	2850	12
3	2700	16
4	2600	22
5	2550	28
6	2400	32
7	2340	45
8	2170	50
9	1930	80

2. Определить скорость воздуха (при 60 °С) в вертикальной трубе-сушилке, обеспечивающую восходящее движение частиц плотностью ρ кг/м³ и диаметром d мм.

№ варианта	ρ , кг/м3	d, мм
0	200	3
1	290	2
2	285	1,2
3	270	1,6
4	260	2,2
5	255	2,8
6	400	3,2
7	340	4,5
8	170	0,8
9	930	8,0

3. Определить массу осадка влажностью 25 %, собирающегося на фильтрующей перегородке в результате фильтрования V м³ суспензии плотностью ρ кг/м³ с массовой долей твердой фазы х %.

№ варианта	ρ , кг/м3	V, м3	х, %
0	1200	5	8
1	1900	7	10
2	1850	9	12
3	1700	11	16
4	1600	14	22
5	1550	12	18
6	1400	8	12
7	1340	6	15
8	1170	17	5
9	1030	4	8

4. Определить необходимую поверхность фильтрования рамного фильтр-пресса для получения V м³ фильтрата в течение T ч, если значения констант фильтрования K = 7,1  10^–7 м²/с и С = = 1,2  10^–3 м³/м².

№ варианта	V, м3	T, час
0	3,2	5
1	2,9	2
2	2,85	3
3	2,7	1,6
4	8,6	7
5	12,4	8
6	7,3	3,2
7	6,0	4,5
8	5,2	5,0
9	4,0	3

5. Определить скорость вертикального потока воздуха, необходимую для начала псевдоожижения слоя сферических частиц алюмосиликагеля размером d мм. Плотность частиц составляет 968 кг/м³. Температура воздуха 100 °С. Определить также перепад статического давления на псевдоожиженном слое, если высота неподвижного слоя составляла H мм.

№ варианта	H, мм	d, мм
0	200	0,8
1	290	1,0
2	360	1,2
3	370	1,6
4	260	2,2
5	550	2,8
6	400	3,2
7	340	4,5
8	470	5,0
9	130	6,0

6. Определить наибольший диаметр гранулированных частиц угля плотностью 660 кг/м³, начинающих переходить во взвешенное состояние в воздухе при скорости потока w м/с и температуре t°С.

№ варианта	w, м/с·102	t°С
0	3,2	50
1	2,9	100
2	8,5	120
3	17	160
4	20	220
5	15	280
6	14	102
7	23	150
8	21	50
9	19,3	80

58