Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский политехнический университет Петра Великого (бывш. СПбГПУ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

матан2сем краткий конспект

.pdf

Скачиваний:

Добавлен:

16.04.2015

Размер:

792.71 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 83 4 5 6 7 8 > Следующая >>>

1. Найти произведения	матриц		ABи			BA,		если	они	существуют.	Сравнить	матрицы
произведения, если
		1		3			1	2	3
		1		3	,			2
	A				,	B 3		2	1 .
		2		1
		2		1			0	2	0
							0	2	0
2. Найти произведения	матриц		ABи			BA,		если	они	существуют.	Сравнить	матрицы
произведения, если							7	5
				3			7	5
				3			6
							6	3
		A	4		,	B	1	2	.
				5
				5		8		1
				6		8		1
				6			5 3
							5 3
3. Найти произведения	матриц		ABи			BA,		если	они	существуют.	Сравнить	матрицы
произведения, если

A 3 , B 1 5 3 4 .5

Практическое занятие №2. Тема. Определители

Цель: Научиться вычислять разными способами определители матрицы.

Пример решения задачи

Задача 1.

а) С помощью теоремы Лапласа.

б) Предварительно упростив, получив нули в какой либо строке (столбце).

2	4	1	3		0 2	5		4	1	3		4	1 3

7	0	2	5
				2	3 5	2	7	3	5	2	3	0	2 5
0	3	5	2
					3 1	3		3 1		3		3	5 2
3	3	1	3

2( 3 ( 2) ( 2) 3 1 5 ( 3 5 5 3 3 ( 2))) 7(4 5 3 3 ( 1) ( 2) 3 1 3(3 5 ( 3) 1 3 3 4 1 ( 2))) 3 (4 ( 2) ( 2) 3 5 ( 1) (3 ( 2) 3 4 5 5))

2( 12 15 ( 75 18)) 7(60 6 9 ( 45 9 8)) 3(16 15 ( 18 100))

2 82 7 125 3 ( 67) 201 164 875 838

Ф КазНПУ 0703-12-09 Учебно-методический комплекс дисциплины для обучающегося

2	4	1 3		1	1	1 6			1	1	6

7	0	2 5		13 6		2 11
								1	13	6	11
0	3	5	2	15 18		5	17
									15	18	17
3	3	1	3	0	0	1	0

1 (1 ( 6) ( 17) 15 1 11 13 18 6 (6 ( 6) ( 15) 1 13 ( 17) 1 11 18))

1 (114 165 1406 ((540 221 198)) 1 (838) 838

Задания

Вычислить определители матрицы.

	2	3	4
		9
1. A 4			7
	3	3	0

	3		2	5	7		1		8	2	4

			2	5			1		9	2	1
2. A	6				9	3. A
		0	1	3	1			0	0	3	1

		1 0		7	0			5	4	8	6

Практическое занятие №3.

Тема. Системы линейных уравнений. Правила Крамера

Цель: Научиться находить решение СЛАУ методом Крамера.

Пример решения задачи

Задача1.

x1 5x2 3x3 2 2x1 x2 x3 1 4x1 2x2 x3 2

						1				5	3

Решение:					A 2					1		1
										2	1
						4				2	1
det A				1	5	3
				1	5	3
				2	1	1			1 20 12 12 10 2				27
				4	2	1
x1	2				5	3
	2				5	3
	1				1 1			2 10 6 6 5 4 23
		2			2	1
x2			1		2	3
			1		2	3
			2		1 1			1 8 12 12 2 4 37
			4		2	1
x3		1			5	2
		1			5	2
		2			1 1		2 20 8 8 20 2 36
		4			2	2

x	23	;x	37	;x	36		4	;
	27		27		27
1		2		3		3
Ф КазНПУ 0703-12-09 Учебно-методический комплекс дисциплины для обучающегося									22

						Задания
x1 x2		2x3			0	4x2 3x3 x4 0
x1 x2		2x3			0		x2	2x3			x4		0
	x1	3x2					x2	2x3			x4		0
1.	x1	3x2			1	2. x x			x		x		0
x x		2	x	3	0		1	2		3		4
	1	2		3			x	2x		2	x		0
							1			2		4

Практическое занятие №4.

Тема. Метод Гаусса. Теорема КронекераКапелли

Цель: Научиться находить решение СЛАУ методом Гаусса.

Пример решения задачи

Задача 1.

a) исследовать на совместимость

б) Найти общее решение методом Гаусса и записать два частных.

3x x x 2x 3x 4
	1		2	3	4			5
2x1 3x2 2x3 x4 4x5 5
x1 2x2 3x3 4x4 x5 3
x1 2x2 3x3 3x3 3x4 7x5 1
1		-2 3 -3			7	-1		1		-2 3 -3 7	-1	1 2		3 3 7		1
1		-2 3 -3			7	-1		1		-2 3 -3 7	-1

1		2 3 4			1	3	0			4 0 7 -6	4		0 4	0 7 6		4
2		3 -2 1			-4	5		0		7 -8 7 -16	7
2		3 -2 1			-4	5		0		7 -8 7 -16	7		0 7	8 7	18	7
		1 1 -2			3	4				7 -8 7 18	7		0 7	8 7	18	7
3		1 1 -2			3	4		0		7 -8 7 18	7
1			2	3	3			7	1
1			2	3	3			7	1
	0		4	0	7		6		4
	0		4	0	7		6		4
	0		0 32		21		30		0

32x3 21x4 30x5 0

2130

x3 32 x4 32 x5

4x2 7x4 6x5 4

x							7		x						6			x			1
x	2								x		4							x	5		1
	2						4				4				4				5
x1 2x2 3x3 3x4 7x5 1
x1		2x2 3x3 3x4 7x5																													7	x4		6		x5					21		x				30	x5	3x4	7x5 1
																										1 2											1 3								4
																										1 2											1 3								4
																															4			4							32						32
			7		x				3x						2								63	x			90	x		3x			7x			1		47	x			38		x			1
					x		4		3x					5	2									x	4			x	5	3x		4	7x		5	1			x	4				x		5	1
		2					4							5								32			4	32			5			4			5		32			4	32					5
x				47				x						19				x			1
x	1							x		4								x		5	1
	1	32								4			16							5
x							7		x						3		x				1
x	2								x		4						x		5		1
	2						4				4				2				5
x						21				x						15				x
x	3									x		4								x		5
	3	32										4			16							5
Частные решения:
Ф КазНПУ 0703-12-09 Учебно-методический комплекс дисциплины для обучающегося																																																			23

x4 32, x5 32, x1 86, x2									4, x3		51
x4 32, x5				32, x1 84, x2						12, x3		51
											Задания
	4x2 3x3 x4 0													x1 x2 x3 x4 x5 0
	x2 2x3 x4 0												x1 x2 x3 2x4 x5 0
	x2 2x3 x4 0												x1 x2 x3 2x4 x5 0
1. x x		2	x	3	x	4		0			2. x 2x				2	x		3	2x		4	4x	5	0
	1	2		3		4							1		2			3			4		5
	x 2x			2	x		4	0					x 2x			2	x		3	x	4	2x	5	0
	1			2			4						1			2			3		4		5

Практические занятия №5, №6.

Тема. Скалярное, векторное и смешанное произведение векторов

Цель: Научиться вычислять и применять скалярное, векторное и смешанное произведение векторов в обычной и координатной форме.

Пример решения задачи

Задача 1. Найти числовое значение выражения

				.				2, если					1
3	m	-2(	m		n	)+4	n			m	=				;	n	= 6, (			,		) =
																			m		n
																							3
										2
3		-2(		.		)+4		2 = 3.	1	- 2.		1		.	6cos(			)+4 . 36 =					3	3+144 = 142	1
	m		m		n		n
2										2					3								2	2

Задача 2. Вычислить площадь параллелограмма, построенного на векторах

a k j , b i j k

Sn = aхb

aхb = (k j )х(i j k ) = k i k j j i j k j 2i k 2i j k

aхb = 1 4 1 6 Sn

Задача 3. Вычислить объем параллелепипеда, построенного на векторах a 3i 4j, b 3j k , c 2 j 5k

3 4 0

V = a b c = 0 3 1 = – 45 – 6 = – 51,

0 2 5

a, b, c = левая тройка векторов.

Задания

1.Дан АВС. АВ{-1,-1,-2 }, ВС{3,3, -6 }. Найти углы .

2.Упростить выражение: a b c c a b c b b c a

3.Вычислить (a b)(a 2b c)(c a )

Практическое занятие №7-8. Тема. Прямая на плоскости

Цель: Научиться узнавать и применять типы уравнение прямой на плоскости.

Задача 1. Найти угловой коэффициент и отрезки, отсекаемые на осях координат для прямой

2x+y+5 = 0

Решение: y 2x 5,	k 2,	x	y	1,	a	5	,	b 5
Решение: y 2x 5,	k 2,	5		1,	a		,	b 5
		5	5		2


		2
Задача 2. Даны вершины АВС, если А(1,5), В(-1,2), С(3,2). Найти высоты.
Ф КазНПУ 0703-12-09 Учебно-методический комплекс дисциплины для обучающегося									24

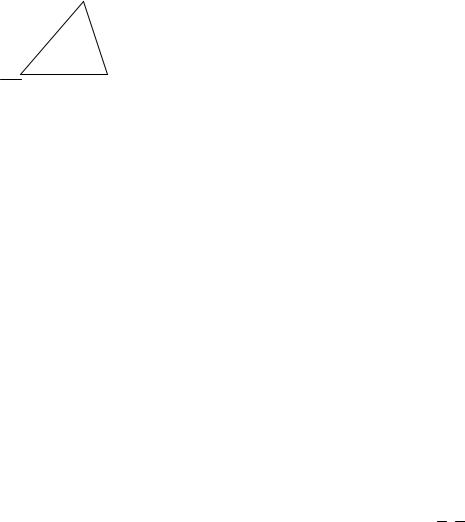
Решение: C

АА1 ВС, ВВ1 АС, СС1 АВ

АВ

2, 3 ,

ВС

4,0 ,

АС

2, 3

ВС- нормаль для АА1, уравнение АА1: 4х + С = 0, т.к.

А АА1, получим С = – 4, АА1: 4х – 4 = 0

Аналогично получим ВВ1: -3y + 8 = =0, СС1 = –2x – 3y + 12 = 0

Задача 3. Определить координаты точки, симметричной т.М (2,-5) относительно прямой 2x + 8y – 15 = 0

Решение:		2,8 ,		2,8 ,	x 2	y 5	,	x 2	y 5
	n		s
					2	8		1	4

или ММ1: 4x – y – 13 = 0. Mo = l ММ12x 8y 15 0

4x y 13 0

							, y 1, x			7
		17y 17 0								7
		17y 17 0
								2
М1: x				x1 x2		, y		y1 y2
М1: x						, y		2
			2					2
	7		2 x2		, x2 5,			1	5 y2		,	y2 7 . Итак М1(5,7).
2					, x2 5,			1			,	y2 7 . Итак М1(5,7).
2			2					2				Задания
												Задания
1. Написать уравнение средних линий АВС с вершинами А(2,6),													В(-4,0), С(4,2).

2.Написать уравнение прямой, проходящей через т.Р(1,2) и отсекающей равные отрезки на осях.

3.Привести к нормальному виду прямую 4x + 3y + 6 = 0.

4.Показать, что ABCD – трапеция, если А(-2,-2), В(-3,1), С( 5,5 ), D(3,1).

2 2

5.Написать уравнение прямой, проходящей через т.А(-1,1) под углом 450 к прямой 2x + 3y = 6.

6.В пучке 3x 4y 1 x y 0найти прямую, проходящую через начало координат.

7.Вычислить площадь ромба, если известна вершина А(-1,3), т.М(0,2), лежащая на стороне АВ

ит.Q(2,1) – т. пересечения диагоналей.

Практическое занятие №9.
Тема. Кривые II – го порядка
Цель: Научиться определять название кривой по каноническому виду.
												Пример решения задачи
		Задача 1. Составить уравнение эллипса, проходящего через точки (2,2), Q(3,1).
		Решение:			x2			y2		1
		Решение:			a2			b2		1
					a2			b2
4		4		9		1					32		a	2	32	,	b		2	32		,		x2	y2
			1						1			3	a			,	b					,				1
	a2	b2		a2			b2				a2				3					5				32 32
																								3	5
		Задача 2.Написать уравнение хорды эллипса																x2			y2		1, проходящей через т. М(2,1), если
		Задача 2.Написать уравнение хорды эллипса															25			16			1, проходящей через т. М(2,1), если
																	25			16
Ф КазНПУ 0703-12-09 Учебно-методический комплекс дисциплины для обучающегося																											25

М – середина.

Решение:

y k x, М диаметру, 1 2k

, k

1 Уравнение диаметра

для

хорды k

, k

уравнение хорды

y y

k(x x )

a2k

y 1

(x 2)

25y 25 32x 64

32x 25y 89 0.

Задача 3. Найти угол между асимптотами гиперболы, если 9.

Решение:

a2 b2

Асимптоты имеют уравнение: y

k2 k1

2 3

b 2

1 k1 k2

arctg(

3) 600

Задача 4. Найти пересечение гиперболы x2

4y2

4 и прямой y x .

Решение:

Решений нет.

3x 4

Задача 5.Найти диаметр параболы y2

4x для хорды, образующей с ОХ угол 450.

Решение: Для хорды k 1, уравнение диаметра y

p 2,

y 2 - -диаметр

параболы.

Задача 6.Найти длину хорды параболы

y2 4x, которая параллельна оси OY и имеет

уравнение х = 1.

Решение: Найдем точки пересечения хорды и параболы: y2

4x, x 1,

y 2

Точки М1(1,2),

М2(1,-2). Длина хорды d

2 2

d 4.

Задача 7.Найти уравнение касательной к гиперболе

1 перпендикулярно к прямой

2x 5y 11 0.

Ф КазНПУ 0703-12-09 Учебно-методический комплекс дисциплины для обучающегося

Решение: Касательная к гиперболе имеет вид xx0 yy0 1. Запишем условие

												9				36
перпендикулярности касательной и данной прямой:													x	0				y	0
												2		0	5				0		0
												2			5						0
												9						36
													x	2		y2
Т. М0(xo, yo) – т. касания, она принадлежит гиперболе														0		0	1.
Т. М0(xo, yo) – т. касания, она принадлежит гиперболе																36	1.
		2		5								9				36
		2	x0	5		y0	0
								5
		9		36						2
Решим систему:		9		36			x0		y0 ,	2	4 16,				y0	8,				x 5
					y02					y0
										y0
	x02						1	8
		9			36		1
		9			36

Уравнение касательных 5x 8y 1 9 36

Задания

1. Определить фокусы, директрисы, эксцентриситет

а)эллипса:	x	2			y2		1
а)эллипса:	25			169			1
	25			169
б)гиперболы			x2			y2
								1
								1

22564

2.Написать касательную к эллипсу

x2 y2 1 в т. М(4,3)

3218

3.Составить уравнение хорды гиперболы x2 y2 1, для которой т. М(5,1)- середина.

4.Написать уравнение касательной к параболе y2 4x в т. (9,6)

5.Найти уравнение диаметра параболы y2 8x для хорд с направление k 2.

Практические занятия №10, №11. Тема. Плоскость

Цель: Научиться определять тип и применять уравнений плоскости.

Пример решения задачи

Задача 1. Написать уравнение плоскости, перпендикулярной к прямой


	x 1	y 1		z 4	и проходящей через точку М(3,-1,2).
3
		2	1						3,2,1.
Решение. Из уравнения прямой выпишем направляющий вектор данной прямой
								s
Этот вектор будет вектором нормали искомой плоскости.						M(x0 , y0 ,z0 ), с вектором
Уравнение			плоскости, проходящей через точку				нормали

n A,B,C имеет вид : A(x x0 ) B(y y0 ) C(z z0 ) 0.

Теперь легко запишем искомое уравнение

3(x-3)+2(y+1)+1(z-2)=0 или 3x-9+2y+2+z-2=0.

Отсюда получим общее уравнение плоскости 3x+2y+z-9=0

Ф КазНПУ 0703-12-09 Учебно-методический комплекс дисциплины для обучающегося

							Задания
1.		Написать уравнение плоскости,					проходящей через точкуM0 (3,5. 2)	и параллельной
плоскости x 2y 5z 0.
2.		Написать уравнение плоскости, проходящей через точку M0 (1,2,0) и перпендикулярной
прямой	x 2			y 1		z 1

		1	1		1
3.		Написать			уравнение плоскости,		проходящей через точку M0 (1,1,1)	и параллельной
координатной плоскости XOY.

Практические занятия №12, №13. Тема. Прямая в пространстве

Цель: Научиться определять тип и применять уравнений прямых в пространстве.

Пример решения задачи

Написать каноническое уравнение прямой, проходящей через точку M0 с направляющим

вектором s		x 1			y 2			z 1
вектором s	2
	2		1			1
Выписать координаты вектора нормали для данной плоскости n 3, 1, 2
Написать каноническое уравнение прямой,														проходящей через точку M0 с направляющим
вектором n .	x 1			y 2			z 1
вектором n .	3			1			2
	3			1			2
Вычислить координаты вектора M0 M1
M0M1	3 ( 1),2 2,4 1 4,0,3
	Написать					каноническое						уравнение			прямой, проходящей через точку M0 с
направляющим вектором M										M		x 1	y 2		z 1	Прямая перпендикулярна оси OY
направляющим вектором M									0	M	1	4	0			Прямая перпендикулярна оси OY
									0		1	4	0	3

Задания

1.Написать уравнение прямой, проходящей через точку M0 (1, 1,1), имеющий

направляющий вектор s 4,0, 1

2. Написать уравнение прямой, проходящей через точку M0 (2, 5,3), параллельную прямой

x 1 y 2 z 3 4 6 9

3. Написать уравнение прямой, проходящей через точку M0 (2,3, 1) перпендикулярно к плоскости x 4y 3z 0

Практические занятия №14, №15. Тема. Комплексные числа

Цель: Научиться совершать действие с комплексными числами в алгебраической и

тригонометрической формах.

Задача 1.

2 5i 1 7i 2 1 5 7i 3 2i

Задача 2. 3 9i 7 i 3 7 9 1 4 10i

Задача 3.

(1 2i)(3 i) 1 3 2( 1) 1( 1) 2 3i 5 5i

Задача 4.

23 i

(23 i)(3 i)

70 20i

7 2i

3 1

(3 i)

Задача 5. a=3(cos

isin),r 3,

Ф КазНПУ 0703-12-09 Учебно-методический комплекс дисциплины для обучающегося

Задача 6.	Записать тригонометрическую форму комплексного числа Решение:
z 4 3i,

r 5,cos 4,sin 3 5 5

z 5(cos isin )

		3
arctg

7.z 1 i

r=		, cos =	1		,sin	1
	2

2				2

2 7 n n

z 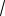2(cos7 isin 7 )или

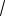2(cos isin ) n n

						Задания
	(1 i)5 (		3	i)10
1.					2. z2 1 0		3.z4	1 0


	(1 i)4 (1 i 3)11
4.z3		1 0			5.z3	1 0	6.z6	1 0
7.z6		1 0			8.z4	1 0	9.z5	1 0

Ф КазНПУ 0703-12-09 Учебно-методический комплекс дисциплины для обучающегося

САМОСТОЯТЕЛЬНАЯ РАБОТА СТУДЕНТОВ ПОД РУКОВОДСТВОМ ПРЕПОДАВАТЕЛЯ (СРСП)

СРСП №1 Тема: Матрицы (3ч.)

Цель: Ознакомиться с учебно-методическим материалом и самостоятельно выполнить теоретические и практические задание.

Задание по теме.

Закрепление усвоенных навыков.

Форма проведения: устный опрос

Методические рекомендации: При подготовке к данному занятию использовать материал лекций № 1, рекомендованную литературу, периодическую печать и информационные ресурсы Internet.

Литература: [3, 4, 6]

СРСП №2 Тема: Определители (3ч.)

Задание по теме.

Закрепление усвоенных навыков.

Форма проведения: устный опрос

Методические рекомендации: При подготовке к данному занятию использовать материал лекций №2, рекомендованную литературу, периодическую печать и информационные ресурсы Internet.

Литература: [3, 4, 6]

СРСП №3 Тема: Системы линейных уравнений. Правила Крамера (3ч.)

Задание по теме.

Закрепление усвоенных навыков.

Форма проведения: устный опрос

Методические рекомендации: При подготовке к данному занятию использовать материал лекций № 3, рекомендованную литературу, периодическую печать и информационные ресурсы Internet.

Литература: [3, 4, 6]

СРСП №4 Тема: Метод Гаусса. Теорема КронекераКапели (3ч.)

Задание по теме.

Закрепление усвоенных навыков.

Форма проведения: устный опрос

Методические рекомендации: При подготовке к данному занятию использовать материал лекций № 4, рекомендованную литературу, периодическую печать и информационные ресурсы

Internet.
Литература: [3, 4, 6]
Ф КазНПУ 0703-12-09 Учебно-методический комплекс дисциплины для обучающегося	30

<<< < Предыдущая 1 23 / 83 4 5 6 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
24.12.2018292.35 Кб13маркетинговые исследования 1.doc
#
21.11.201875.63 Кб7мат вед.docx
#
25.11.2019747.52 Кб4мат-стат-а.doc
#
21.04.2019445.95 Кб20матан 2й курс 1й сем часть 1.doc
#
21.04.2019348.16 Кб6матан 2й курс 1й сем часть 2.doc
#
16.04.2015792.71 Кб23матан2сем краткий конспект.pdf
#
08.05.2019869.38 Кб10Матвед.doc
#
24.09.2019488.96 Кб35матвед.doc
#
12.09.2019636.42 Кб4Математика Экзамен1.doc
#
16.04.201522.02 Кб12матер-литература.doc
#
15.11.201869.94 Кб2Материал для подготовки к экзамену по физике.docx