59. Интегральный признак Коши. Интегральный признак Коши.

Пусть - знакоположительный числовой ряд. Составим функцию непрерывного аргументаy = f(x), аналогичную функции. Пусть функцияy = f(x)положительная, непрерывная и убывающая на интервале, где). Тогда в случае сходимостинесобственного интеграла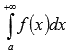сходится исследуемый числовой ряд. Если же несобственный интеграл расходится, то исходный ряд тоже расходится. При проверке убывания функцииy = f(x)на интервалеВам может пригодится теория из разделавозрастание и убывание функции.Пример. Исследуйте числовой ряд с положительными членамина сходимость.Решение. Необходимое условие сходимости ряда выполнено, так как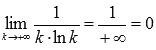. Рассмотрим функцию. Она положительная, непрерывная и убывающая на интервале. Непрерывность и положительность этой функции не вызывает сомнения, а на убывании остановимся чуть подробнее. Найдем производную: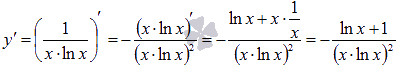. Она отрицательная на промежутке, следовательно, функция убывает на этом интервале. Таким образом, функцияудовлетворяет всем условиям интегрального признака Коши. Воспользуемся им: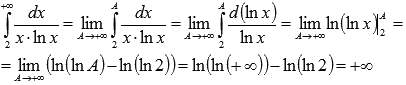То есть, несобственный интеграл расходится, следовательно, расходящимся является исходный числовой ряд.

59. Признаки Куммера, Даламбера, Раабе. Признак Куммера

Пусть дан ряд 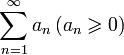и произвольная числовая последовательность, такая что рядрасходится. Тогда рядсходится, если для некотороговыполняется неравенство:

,

где .

Если же для, то ряд расходится.

Доказательство

Дан ряд .

1.Пусть для всех выполняется неравенство:

.

Домножив обе части этого неравенства на , получим:, (*)

а поскольку , то:

,

.

Отсюда следует, что последовательность монотонно убывает и,следовательно, стремится к конечному пределу (так как она ограничена снизу нулём). Соответственно, сходится и последовательность), которая является суммойпервых членов ряда, который в силу этого также сходится.

Но тогда из неравенства (*), по первой теореме сравнения, следует, что сходится ряд . Тогда, поскольку, должен сходится и данный ряд.

2.Пусть теперь для некоторого выполняется неравенство:

или

.

Разделив обе части этого неравенства на получим:

.

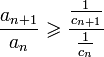Так как по условиям теоремы ряд предполагается расходящимся, то в силу теоремы сравнения, должен расходиться и данный ряд.

Формулировка в предельной форме

Если существует предел: то при ряд сходится, а при— расходится.

Признак Даламбера.

Пусть- знакоположительный числовой ряд. Если, то числовой ряд сходится, если, то ряд расходится.Замечание.Признак Даламбера справедлив, если предел бесконечен, то есть, если, то ряд сходится, если, то ряд расходится. Если, то признак Даламбера не дает информацию о сходимости или расходимости ряда и требуется дополнительное исследование. Пример. Исследуйте числовой ряд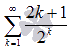на сходимость по признаку Даламбера. Решение. Проверим выполнение необходимого условия сходимости числового ряда, предел вычислим поправилу Лопиталя: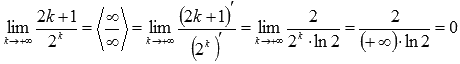Условие выполнено. Воспользуемся признаком Даламбера: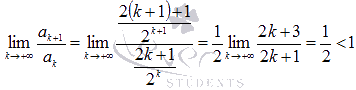Таким образом, ряд сходится. Пример. Проверьте расходимость числового ряда. Решение. 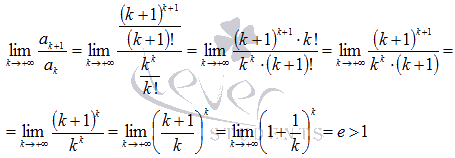Воспользуемся признаком Даламбера для исследования сходимости числового ряда: Следовательно, ряд расходится. В последнем переходе мы использовали второй замечательный предел.