4. Числовые и функциональные ряды.

59. Числовые ряды. Сходимость и расходимость ряда. Сумма и остаток сходящегося ряда. Определение

Пусть — числовая последовательность; рассмотрим наравне с данной последовательностью последовательность

каждый элемент которой представляет собой сумму некоторых членов исходной последовательности. В наиболее простом случае используются обычные частичные суммы вида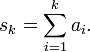

Вообще, для обозначения ряда используется символ поскольку здесь указана исходная последовательность элементов ряда, а также правило суммирования.

В соответствии с этим говорится о сходимости числового ряда:

числовой ряд сходится, если сходится последовательность его частичных сумм;

числовой ряд расходится, если расходится последовательность его частичных сумм:

числовой ряд сходится абсолютно, если сходится ряд из модулей его членов.

Если числовой ряд сходится, то предел последовательности его частичных сумм носит названиесуммы ряда:

Операции над рядами

Пусть заданы сходящиеся ряды и . Тогда:

Их суммой называется ряд

Их произведением по Коши называется ряд , где

Если оба ряда сходятся, то их сумма сходится, если оба ряда сходятся абсолютно, то их сумма сходится абсолютно. Если хотя бы один из рядов сходится абсолютно, то произведение рядов сходится.

Критерий абсолютной сходимости

Ряд сходится абсолютно тогда и только тогда, когда сходятся оба положительных рядаиГде

Доказательство.Если сходитсято по признаку сравнения тем более сходятсяиНаоборот, если сходятсяито сходится и их сумма

Введем важное понятие остаткаряда. Именно, если a₁ + a₂ + a₃ + a₄ + ...     (18)

есть некоторый ряд, а m- какое-нибудь натуральное число, то остатком ряда (8) послеm-го члена называется рядa_m+1+a_m+2+a_m+3+ ...     (19)

     Теорема 4. Сам ряд и его остаток сходятся или расходятся одновременно.

     В самом деле, пусть частичные суммы рядов (18) и (19) суть соответственно S_nи. Тогда приn>m (20)

     Допустим, что остаток (19) сходится и его сумма равна R_m. Тогда при стремленииnк бесконечности будет

откуда следует, что S_n→S_m+R_m. Иначе говоря, ряд (18) также сходится, и его сумма естьS=S_m+R_m.     (21)

     Обратно, если сходится ряд (18) и сумма его равна S, то из того же соотношения (20) вытекает, что

 Если ряд сходится, то, как это видно из равенства (21), сумма его остатка после m-го члена в точности равна разности между суммойSвсего ряда и его частичной суммойS_m. Так как при возрастанииmчастичная суммаS_mбудет стремиться кS, то отсюда следует

     Теорема 5. Сумма остатка сходящегося ряда послеm-го члена стремится к нулю при возрастанииm

     В заключение докажем одно, часто используемое, необходимое условие сходимости ряда.

     Теорема 6. Общий член сходящегося ряда при возрастании своего номера стремится к нулю.

     Иными словами, из сходимости ряда a₁+a₂+a₃+ ...     (22)

вытекает, что      (23)

     Действительно, если сумму ряда (22) обозначить через S, то с возрастаниемnкаждая из суммS_n=a₁+a₂+ ...+ a_n,     S_n-1 = a₁ + a₂ + ... +a_n-1

будет стремиться к S. Но тогдаS_n-S_n-1 →S-S= 0,

и остается заметить, что S_n-S_n-1 =a_n.

     Весьма важно подчеркнуть, что условие (23), будучи необходимым для сходимости ряда (22), вовсе не является для этой сходимости достаточным. В самом деле, гармонический ряд удовлетворяет усл. 23, но расходится.