15.2. Эффективное сечение рассеяния.

Определение: Эффективное сечение рассеяния - величина, характеризующая вероятность перехода системы сталкивающихся частиц в результате их рассеяния (как упругого, так и неупругого) в определенное конечное состояние.

Конечное состояние каждой частицы пучка характеризуется углом , под которым она рассеялась. Обозначим через число частиц, рассеиваемых в единицу времени на углы, лежащие в интервале от до .

Само значение 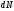зависит от числа падающих

Пучок

частиц, точнее от плотности частиц в потоке, и

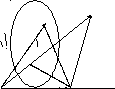
поэтому его неудобно использовать для

характеристики процесса рассеяния.

Пусть 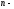плотность падающих частиц, а

их скорость в направлении движения пучка.

Тогда число падающих на поперечную площадку частиц за время равно

,

т.е. числу частиц, находящихся в объеме

.

Значит, за единицу времени через единицу площади площадки проходит

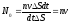частиц,

где плотность потока частиц.

В этом случае эффективное сечение рассеяния определяется как

(15.5)

Размерность сечения равна размерности площади, т.к. 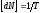, , 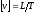, откуда получаем .

Величина эффективного сечения (15.5) полностью определяется видом рассеивающего поля и является важнейшей характеристикой процесса рассеяния. Эта характеристика измеряется экспериментально и служит для определения структуры сталкивающихся частиц.

Если связь между переменными и взаимно

однозначна, как это имеет место в классической

механике, то под углами, лежащими от до

, рассеиваются только те частицы, которые

летят в некотором интервале значений прицельного

расстояния от до (угол рассеяния

монотонно убывает с ростом прицельного расстояния).

Тогда число частиц, рассеивающихся в единицу

времени в интервал углов (), равно

. (15.6)

Т.о., сечение рассеяния может быть выражено через

прицельное расстояние как

. (15.7)

Часто бывает удобно характеризовать сечение углами,

под которыми вылетают частицы:

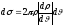. (15.8)

Частицы, испытавшие рассеяние на силовом центре, продолжают свое движение, распределяясь в некоторой

области пространства. Поэтому для описания задачи наряду с плоскими вводят телесные (пространственные)

углы.

Элементарный телесный угол определяется как

, (15.9)

где элемент поверхности сферы радиуса .

Любая поверхность , опирающаяся на элемент

, характеризуется тем же телесным углом .

Любой замкнутой сферической поверхности, от центра которой ведется отсчет, соответствует телесный угол, равный

. (15.10)

Т.о., полный телесный угол равен .

В задачах рассеяния телесный угол, вырезающий область пространства, в пределах которого разлетаются частицы в результате взаимодействия с силовым центром, имеет форму раструба – конусный угол.

Найдем связь между телесным углом , характеризующим результат рассеяния и параметрами столкновения и .

Площадь элемента сферической поверхности,

вырезаемый конусами, задаваемыми углами

и , равна

поэтому

. (15.11)

Тогда сечение рассеяния (дифференциальное сечение):

. (15.12)

Зная зависимость , получим сечение рассеяния как функцию угла 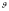. Чтобы найти полное сечение рассеяния , надо проинтегрировать (15.12) по всем углам.