
1.14. Задача двух тел.
В предыдущем параграфе рассматривалось движение частицы в поле с неподвижным центром. Ниже мы рассмотрим различные случаи столкновения двух частиц, представляющие большой практический интерес, и покажем, что такие задачи можно формально свести к рассмотрению движения одной частицы в поле центральных сил.
Иное название рассматриваемой проблемы – задача двух тел. Отметим, что только для двух взаимодействующих тел поставленная задача имеет аналитическое решение в общем виде.
-
Взаимодействие двух частиц. Приведенная масса.
Рассмотрим взаимодействие двух частиц, которые образуют замкнутую систему. Задачу о движении этих частиц удобнее решать в системе центра инерции (СЦИ). Центр инерции замкнутой системы частиц, как это следует из закона сохранения импульса либо находится в покое, либо движется равномерно и прямолинейно. Поэтому СЦИ является инерциальной системой отсчета.
Радиус-вектор (координаты) центра инерции определяется как (см. рисунок):
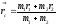 (14.1)
(14.1)
Если
начало отсчета поместить в центр инерции
системы, то
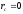 и из (14.1) имеем
и из (14.1) имеем
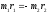 .
(14.2)
.
(14.2)
Введем
в рассмотрение вектор
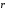 ,
характеризующий относительное положение
частиц:
,
характеризующий относительное положение
частиц:
 .
(14.3)
.
(14.3)
Тогда, используя уравнения (14.2) и (14.3) можем записать
 (14.4)
(14.4)
Согласно третьему закону Ньютона силы взаимодействия между частицами:
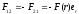 .
(14.5)
.
(14.5)
Запишем
уравнения динамики для каждой из
взаимодействующих частиц (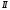 закон Ньютона):
закон Ньютона):
 ,
(14.6)
,
(14.6)
Перенеся массы частиц в уравнениях (14.6) в правую часть, вычтем первое уравнение из второго. Получаем

Итак, получаем уравнение движения в виде:
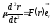 ,
(14.7)
,
(14.7)
где
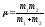 - приведенная
масса системы
частиц.
- приведенная
масса системы
частиц.
Формально мы
перешли к задаче о движения одной частицы
массой
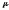 в поле сил
в поле сил
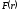 .
.
Т.о.,
любая задача о движении двух
взаимодействующих тел сводится
к задаче о движении одного
тела с массой, равной приведенной массе
системы частиц, в центральном поле сил.
Поэтому все результаты, полученные в
предыдущем параграфе, могут быть
использованы при решении этой задачи.
Определяя
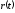 или
или
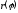 ,
и находя далее
,
и находя далее
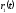 и
и
 ,
получаем те же плоские траектории:
эллипсы, параболы и гиперболы.
,
получаем те же плоские траектории:
эллипсы, параболы и гиперболы.
Примеры
двойные системы звезд, позитроний, рассеяние заряженных частиц.
Столкновения частиц
Столкновения частиц подразделяют на упругие, при которых не происходит изменения внутренней энергии частиц, и неупругие, в результате которых внутренняя энергия взаимодействующих частиц изменяется. Существует большое число неупругих столкновений, в которых внутренняя энергия частиц может изменяться только на вполне определенную величину, зависящую от свойств самих частиц (например, столкновения атомов). Говорят, что такие взаимодействия обладают порогом. Порогом называют минимальную кинетическую энергию налетающей частицы, начиная которой проводимый процесс становится энергетически возможным.
14.2. Неупругие столкновения
Распад частиц.
Рассмотрим обратный
абсолютно неупругому столкновению
процесс, называемый распадом частицы,
и опишем его в лабораторной системе
отсчета ( система) и в системе центра инерции
(
система) и в системе центра инерции
( cистема).
cистема).
Очевидно, что
наиболее простое описание получает
этот процесс в системе центра инерции.
В
 системе
частицы, образовавшиеся в результате
распада, уносят одинаковое количество
движения, двигаясь в противоположные
стороны. Тогда в
системе
частицы, образовавшиеся в результате
распада, уносят одинаковое количество
движения, двигаясь в противоположные
стороны. Тогда в
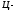 системе
закон сохранения импульса можно записать
как
системе
закон сохранения импульса можно записать
как
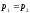 и пусть
и пусть
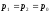 .
.
Поскольку исходная
частица в
 системе
покоится, её полная энергия равна
внутренней. В этом случае закон сохранения
энергии (с учетом внутренней энергии
образовавшихся частиц) имеет вид:
системе
покоится, её полная энергия равна
внутренней. В этом случае закон сохранения
энергии (с учетом внутренней энергии
образовавшихся частиц) имеет вид:
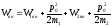 ,
(14.8)
,
(14.8)
Введем энергию
распада
 как энергию, перешедшую при распаде из
внутренней энергии исходной частицы в
кинетическую энергию осколков:
как энергию, перешедшую при распаде из
внутренней энергии исходной частицы в
кинетическую энергию осколков:
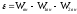 (14.9)
(14.9)
Учитывая (14.8), получаем
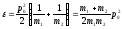
Т.е.
в
 системе
энергию распада частицы можно представить
как кинетическую энергию частицы с
приведенной массой
системе
энергию распада частицы можно представить
как кинетическую энергию частицы с
приведенной массой
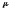 :
:
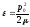 (14.10)
(14.10)
Если
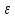 известно, то находим
известно, то находим
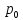 и скорости частиц в СЦИ:
и скорости частиц в СЦИ:
 (14.11)
(14.11)
Примечание: уравнения (14.10)-(14.11) справедливы для абсолютно неупругого удара, если процесс рассматривать в СЦИ.
Вернемся в
лабораторную
систему отсчета (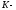 система),
поскольку
именно полученные в ней результаты
представляют практический интерес.
система),
поскольку
именно полученные в ней результаты
представляют практический интерес.
Используя полученные
в СЦИ результаты, определим в лабораторной
системе отсчета возможные углы вылета
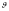 одной из образовавшихся частиц
относительно направления движения
исходной частицы.
одной из образовавшихся частиц
относительно направления движения
исходной частицы.
Пусть
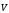 - скорость в
- скорость в
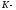 системе
исходной частицы,
системе
исходной частицы,
 - скорость в
- скорость в
 системе
одной из образовавшихся частиц,
системе
одной из образовавшихся частиц,
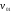 - ее скорость в
- ее скорость в
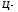 системе.
Тогда, следуя преобразованиям Галилея
для скорости первого “осколка”, имеем
следующее соотношение:
системе.
Тогда, следуя преобразованиям Галилея
для скорости первого “осколка”, имеем
следующее соотношение:
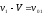 ,
(14.12)
,
(14.12)
возводя в квадрат, получаем
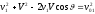 .
(14.13)
.
(14.13)
Здесь
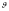 и есть угол вылета частицы по отношению
к скорости первоначальной частицы.
Поэтому уравнение (14.13) определяет
зависимость скорости образовавшейся
в результате распада частицы от
направления ее вылета в
и есть угол вылета частицы по отношению
к скорости первоначальной частицы.
Поэтому уравнение (14.13) определяет
зависимость скорости образовавшейся
в результате распада частицы от
направления ее вылета в
 системе.
Эту зависимость можно проанализировать
эти графически с помощью диаграмм.
системе.
Эту зависимость можно проанализировать
эти графически с помощью диаграмм.
Построим окружность
радиусом
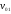 .
Затем к центру окружности проводим
вектор
.
Затем к центру окружности проводим
вектор
 .
Тогда, исходя из (14.12), скорость
.
Тогда, исходя из (14.12), скорость
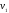 образовавшейся частицы определяется
вектором, проведенным из точки
образовавшейся частицы определяется
вектором, проведенным из точки
 в какую-либо точку окружности (точнее
– сферы, диаметральным сечением которой
является изображенная окружность).
в какую-либо точку окружности (точнее
– сферы, диаметральным сечением которой
является изображенная окружность).
На диаграммах
рассмотрены случаи, когда скорость
распадающейся частицы в
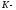 системе
меньше
системе
меньше
(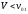 ,
рис. слева) или больше (
,
рис. слева) или больше ( ,
рис. справа) скорости образующейся
частицы в
,
рис. справа) скорости образующейся
частицы в
 системе.
системе.
При
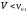 ,
как следует из изображенной слева
диаграммы, частица может вылететь под
любым углом
,
как следует из изображенной слева
диаграммы, частица может вылететь под
любым углом
 .
В случае же
.
В случае же
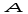 (правая диаграмма) частица может вылететь
только вперед, под углом
(правая диаграмма) частица может вылететь
только вперед, под углом
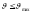 .
Предельное значение угла вылета частицы
задается равенством:
.
Предельное значение угла вылета частицы
задается равенством:
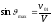 .
(14.14)
.
(14.14)
и
определяет направление касательной к
окружности, проведенной из точки
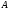 .
.
Связь между углами
вылета
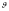 и
и
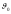 в
в
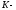 и
и
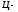 системах
определяется из тех же диаграмм и дается
выражением:
системах
определяется из тех же диаграмм и дается
выражением:
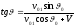 .
(14.15)
.
(14.15)
Решая это уравнение
относительно
 ,
после элементарных преобразований
получим
,
после элементарных преобразований
получим
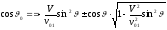 .
(14.16)
.
(14.16)
При
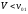 связь между углами
связь между углами
 и
и
 ,
как это видно из левого рисунка,
однозначна. В этом случае в выражении
(14.16) перед вторым слагаемым надо выбрать
знак
,
как это видно из левого рисунка,
однозначна. В этом случае в выражении
(14.16) перед вторым слагаемым надо выбрать
знак
 ,
чтобы при
,
чтобы при
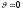 было
было
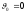 .
.
Если же
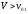 ,
то связь между углами
,
то связь между углами
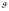 и
и
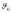 неоднозначна. Как видно из правого
рисунка, каждому значению
неоднозначна. Как видно из правого
рисунка, каждому значению
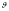 отвечают два значения
отвечают два значения
 ,
соответствующие векторам
,
соответствующие векторам
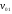 ,
проведенным из центра окружности в
точки
,
проведенным из центра окружности в
точки
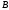 и
и
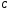 ,
и, соответственно, два знака перед вторым
слагаемым в выражении (14.16).
,
и, соответственно, два знака перед вторым
слагаемым в выражении (14.16).
