14.3. Упругие столкновения

Столкновение двух частиц называется упругим, если оно не сопровождается изменением их внутреннего состояния. Поэтому при описании упругого соударения в законе сохранения энергии внутреннюю энергию тел можно не учитывать.

Выберем лабораторную систему отсчета, где одна из частиц обладает импульсом 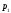, а вторая до соударения покоится (), и запишем законы сохранения энергии и импульса:

(14.17а)

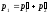. (14.17б)

Выразим 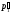из уравнения (14.17б) и подставим в уравнение (14.17а):

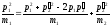
Введя угол 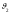между векторами и 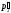, выразим :

. (14.18)

Полученный результат можно интерпретировать графически с помощью векторных диаграмм, построенных для различных соотношений масс сталкивающихся частиц:

; и .

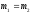Обозначим

, (14.19)

где приведенная масса, скорость налетающей частицы (вторая частица покоится ),

и проведем окружность радиусом . Построим вектор .

Из (14.19) следует

. (14.20)

Направленный отрезок на диаграмме изображает импульс налетающей частицы до рассеяния. При этом точка лежит внутри (если ), вне (если 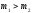) или на окружности (если ).

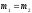Из (14.20) видно, что складывается из отрезков и , пропорциональных массам сталкивающихся частиц, и , соответственно.

В свою очередь из (14.18) следует, что диаметр окружности, равный

,

будучи умноженным на , дает вектор (см. рисунок: как угол, вписанный в окружность).

Из уравнения (14.17б) следует, что вектору на диаграмме соответствует отрезок, направленный из точки в точку . Тогда 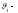угол отклонения 1-ой частицы (налетающей) от её первоначального направления движения после столкновения.

Угол угол разлета 1 и 2-ой частиц после столкновения.

Возможные направления рассеяния первой частицы определяются вращением вектора вокруг точки . При этом конец вектора (точка ) всегда должен лежать на окружности радиусом .

При угол рассеяния может принимать значения от до , а угол разлета изменяется от до .

При очевидно, что существует максимальный угол отклонения налетающей частицы , определяемый точкой касания вектором окружности:

.

угол разлета в этом случае изменяется от до .

Угол соответствует центральному удару, или лобовому столкновению частиц.

При все точки начала и конца векторов лежат на

окружности. Угол 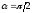, т.е. разлет частиц происходит под

прямым углом. В этом случае .

Исключением является лобовое столкновение, при котором

.

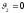Тот же результат можно получить аналитически, решая

совместно уравнения законов сохранения энергии и импульса:

,

.

Возводя в квадрат второе уравнение и сравнивая его с первым, легко убедиться, что совместно эти уравнения могут быть удовлетворены лишь при указанных значениях углов.

На всех рисунках центральный угол представляет собой угол поворота первой частицы в системе центра инерции. Из рисунков видно, что углы 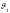и связаны с углом соотношениями:

, .

Модули скоростей частиц после столкновения выражаются через угол и скорость налетающей частицы следующим образом:

, ,

где .

1.15. Рассеяние частиц.

15.1. Рассеяние частицы на силовом центре. Формула Резерфорда.

Рассмотрим снова рассеяние частицы на силовом центре.

Если на налетающую частицу действуют силы отталкивания, то, как мы установили в § 13, её движение всегда инфинитно, а траектория частицы - гипербола.

Для рассмотрения задачи введем

прицельное расстояние – длина

перпендикуляра, опущенного из

рассеивающего центра на направление

касательной к траектории (асимптоту гиперболы)

находящейся на бесконечно большом удалении

от центра частицы,

угол рассеяния частицы,

масса частицы,

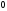
скорость налетающей частицы на

бесконечно большом удалении от центра.

Угол 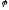определяет наклон асимптот гиперболы, по которой движется рассеиваемая частица (см. рисунок и уравнение (13.17)), к оси и связан с углом рассеяния очевидным соотношением

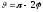(15.1)

Значение угла может быть найдено из уравнения (13.17), если положить, что частица находится на бесконечно большом удалении от рассеивающего центра (). В этом случае уравнение (13.17) приводится к виду:

и . (15.1а)

Тогда, с учетом (15.1) и (15.1а),

.

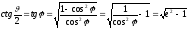Учитывая (13.5), находим связь между углом рассеяния и характеристиками частицы и поля:

. (15.2)

На бесконечно большом расстоянии от рассеивающего центра (, ), полная энергия и момент импульса частицы равны

. (15.3)

Подставляя эти величины в выражение (15.2), получаем формулу, связывающую угол рассеяния с прицельным параметром :

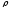. (15.4)

Заметим, что при движении частицы в поле притяжения () связь между углом рассеяния и прицельным параметром получается точно такой же, т.е. также выражается формулой (15.4).

Задача о рассеянии на силовом центре имеет важное практическое значение. Однако, формулу (15.4) не удается непосредственно использовать для описания результатов эксперимента, т.к. она написана для определенного прицельного параметра и определяет индивидуальное отклонение частицы. В эксперименте же мы имеем дело не с отдельной частицей, а наблюдаем рассеяние целого пучка одинаковых частиц, падающих на рассеивающий центр с одинаковыми скоростями , но с разными значениями прицельного параметра . Следовательно, и рассеиваются частицы под разными углами .

Поэтому в физике вводится другая, очень важная, характеристика процесса рассеяния - сечение или эффективное сечение.