
- •ГЛАВА 1. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ
- •§ 1. Основные понятия теории устойчивости
- •t – независимое переменное (время),
- •– искомые функции переменной t (фазовые переменные),
- •Перепишем дифференциальную систему (1) в векторной форме:
- •2о. Основные определения.
- •2) для этих решений выполняется неравенство
- •Рис. 1.3. Иллюстрация к замечанию 3.
- •1) это решение устойчиво по Ляпунову и, кроме того,
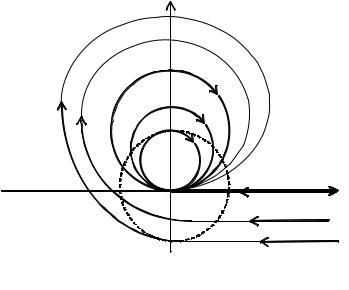
- •Не следует думать, что равенство (2) из условия 2) всегда влечет устойчивость, т.е. условие 1). Рассмотрим, например, систему второго порядка (фазовый портрет которой представлен на рис. 1.4):
- •Необходимо отметить, что системы, фазовый портрет которых в общих чертах весьма похож на описанный выше, действительно существуют (см. [1]).
- •Выполняется замена переменных
- •О п р е д е л е н и е 7. Систему
- •Приведем формулировку устойчивого нулевого решения.
- •40. Примеры.
- •Можно записать
- •2) Исследуем на устойчивость нулевое решение уравнения
- •то для наличия устойчивости нужно, чтобы имело место неравенство
- •Упражнения
- •2) Исследовать на устойчивость решения следующих дифференциальных уравнений с указанными начальными данными:
- •3) Установить равномерную устойчивость нулевого решения с.д.у.
- •§ 2. Общие теоремы об устойчивости линейных систем
- •Линейная система дифференциальных уравнений имеет вид
- •Для системы (1) выпишем соответствующую однородную систему
- •О п р е д е л е н и е 1. Линейную систему (1) называют устойчивой (вполне неустойчивой), если все её решения устойчивы (соответственно – неустойчивы) по Ляпунову.
- •З а м е ч а н и е 1. Определение 1 корректно, поскольку, как будет показано далее, все решения линейных систем одновременно либо устойчивы, либо неустойчивы.
- •Следствие 1. Линейная система (1) устойчива, если устойчиво хотя бы одно решение этой системы, и вполне неустойчива, если неустойчиво некоторое её решение.
- •На основании теоремы 1 исследование устойчивости линейных систем всегда можно ограничить лишь классом однородных систем; именно это и будет сделано в следующем параграфе.
- •О п р е д е л е н и е 2. Линейная система (1) называется асимптотически устойчивой, если асимптотически устойчивы все её решения.
- •Следствие 2. Линейная система (1) асимптотически устойчива, если таковым является хотя бы одно решение этой системы (в частности, её нулевое решение).
- •Упражнения
- •1) Установить асимптотическую устойчивость линейной системы
- •2) Проверить, что всякое устойчивое решение системы (1) равномерно устойчиво по Ляпунову.
- •4) Доказать, что если линейная система (1) асимптотически устойчива, то всякое её решение асимптотически устойчиво в целом.
- •§ 3. Устойчивость линейных однородных систем
- •Как показывает следующая теорема, устойчивость линейной однородной системы (1) эквивалентна ограниченности всех её решений (что равносильно ограниченности её какой-либо фундаментальной матрицы).
- •где M – некоторое положительное число.
- •Полученное означает устойчивость нулевого решения системы (1). Следовательно, по теореме 1 предыдущего параграфа устойчиво любое её решение.
ГЛАВА 1. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ_______________________________________________20
|
|
|
|
yδ (t0 )−η(t0 ) |
|
|
|
< δ, |
|
|
|
|
yδ(t1 )− η(t1 ) |
|
|
|
≥ ε. |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Существует более «сильная» форма устойчивости, чем простая устойчи- |
|||||||||||||||||||||||||||||||||
вость по Ляпунову; она вводится следующим определением. |
|
||||||||||||||||||||||||||||||||
О п р е д е л е н и е |
4. Решение |
η = η(t) |
( t ≥ 0) системы (1) называют |
||||||||||||||||||||||||||||||
асимптотически устойчивым по Ляпунову при t → +∞, если |
|
||||||||||||||||||||||||||||||||
1) |
это решение устойчиво по Ляпунову и, кроме того, |
|
|||||||||||||||||||||||||||||||
2) |
для любого t0 ≥ 0 |
существует такое |
= (t0 )> 0 , что все решения |
||||||||||||||||||||||||||||||
|
y = y(t), удовлетворяющие неравенству |
|
y(t0 )−η(t0 ) |
|
|
|
< |
, обладают |
|||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
|
предельным свойством |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
lim |
|
|
|
y(t) − η(t) |
|
|
|
|
= 0 . |
|
|
|
|
|
|
|
|
(2) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
t→+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Не следует думать, что равенство (2) из условия 2) всегда влечет устойчивость, т.е. условие 1). Рассмотрим, например, систему второго порядка (фазовый портрет которой представлен на рис. 1.4):
dx = P(x, y), |
|
|
|
|
||
dt |
|
|
|
|
|
(*) |
|
= Q(x, y), |
|
|
|
||
dy |
|
|
|
|
||
dt |
|
|
|
|
|
|
с функциями P, Q , непрерывными на |
R2 |
и обладающими свойством P(0,0) = |
||||
Q(0,0) = 0. |
|
Здесь |
начало |
координат |
||
y |
|
|||||
|
является |
положением равнове- |
||||
|
|
|||||
|
|
сия. Одна из траекторий пред- |
||||
|
|
ставляет собой |
положительную |
|||
|
|
полуось Ox (без нуля), но с про- |
||||
|
|
тивоположным |
направлением |
|||
|
|
при t → +∞. Еще одна траекто- |
||||
|
|
рия имеет вид окружности, ка- |
||||
|
|
сающейся как оси абсцисс, так и |
||||
|
|
окружности, |
|
изображенной |
||
|
|
x пунктирной линией; траектория, |
||||
|
|
отвечающая |
этой |
окружности |
||
|
|
асимптотически выходит из на- |
||||
Рис. 1.4. Фазовый портрет системы (*). |
чала координат и таким же об- |
|||||
|
|
разом при |
t → +∞ |
к нему при- |
||
ближается. Имеются траектории в четвертой четверти, параллельные оси абсцисс и противоположные ей по направлению; доходя до оси ординат, они затем как бы «наматываются» снаружи на указанную выше окружность и стремятся к
ГЛАВА 1. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ_______________________________________________21
началу координат при t → +∞. Остальная часть траекторий представляет собой окружности без начала координат, касающиеся оси абсцисс и расположенные внутри отмеченного пунктиром круга. В итоге, через каждую точку фазовой плоскости проходит одна и только одна траектория.
Все траектории, отличные от положения равновесия, стремятся к началу координат при t → +∞, но в любой сколь угодно малой окрестности нуля существуют кривые (проходящие под осью абсцисс), которые в какой-то момент времени покидают пределы отмеченного пунктиром круга с центром в начале координат. Это означает, что условие 2) из определения асимптотической устойчивости выполнено, тогда как условие 1) нарушается.
Необходимо отметить, что системы, фазовый портрет которых в общих чертах весьма похож на описанный выше, действительно существуют (см. [1]).
З а м е ч а н и е 5. При наличии свойства интегральной непрерывности проверка асимптотической устойчивости (так же, как и простой устойчивости) заданного решения аналогична проверке этого свойства решения лишь для не-
которого t0 ≥ 0 .
О п р е д е л е н и е 5. Пусть решение η = η(t) (t ≥ 0) системы (1) асим-
птотически устойчиво по Ляпунову. При заданном t0 ≥ 0 |
множество всех то- |
||||||||
чек y0 Rn , для которых выполняется равенство |
|
||||||||
lim |
|
|
|
y(t; t0 , y0 ) −η(t) |
|
|
|
= 0 , |
(2) |
|
|
|
|
||||||
t→+∞ |
|
|
|
|
|
|
|
|
|
называют областью асимптотической устойчивости (областью притяжения) |
||||
решения η(t). |
|
|
||
|
Здесь |
y = y(t;t0 , y0 ) – |
решение |
системы (1) с начальными данными |
(t0 , y0 ) , т.е. y(t0;t0 , y0 ) = y0 . |
|
|
||
|
О п р е д е л е н и е 6. |
Пусть правая часть системы (1) задана при всех |
||
t0 ≥ 0 |
и y Rn . Если решение η= η(t) |
асимптотически устойчиво и для лю- |
||
бого |
t0 ≥ 0 |
область притяжения совпадает со всем фазовым пространством |
||
Rn , то данное решение называют асимптотически устойчивым в целом.
30. Система в отклонениях. Исследование устойчивости частного решения η= η(t) системы (1) обычно сводят к исследованию устойчивости нулевого решения некоторой другой системы. Осуществляется это так.
Выполняется замена переменных |
|
y(t) = x(t) + η(t), |
t ≥ 0 , |
где x(t) – новая искомая вектор-функция. Тогда |
|
ГЛАВА 1. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ_______________________________________________22
|
dy |
= |
|
dx |
+ |
dη |
= |
dx |
+f (t, η(t))= f (t, x + η(t)) . |
|
|
|
|
|
dt |
dt |
|
|
|||||
|
dt |
|
|
dt |
|
||||||
|
|
|
|
|
|
|
|
1444442444443 |
|
||
|
|
|
|
|
|
|
|
(3) |
|
||
О п р е д е л е н и е 7. Систему |
|
||||||||||
|
|
dx |
|
= f (t, x + η(t)) −f (t, η(t))=: Q(t, x) |
(3) |
||||||
|
|
|
dt |
||||||||
|
|
|
|
|
|
|
|
|
|
||
называют системой в отклонениях. Здесь Q(t,0) = 0 для всех |
t ≥ 0 , т.е. сис- |
||||||||||
тема (3) имеет нулевое решение |
x ≡ 0 . |
|
|||||||||
Решению η= η(t) |
системы (1) при выполнении указанного преобразова- |
||||||||||
ния переменных соответствует нулевое решение x ≡ 0 системы в отклонениях
(3). Причем оба решения с точки зрения устойчивости ведут себя совершенно одинаково: решение η= η(t) системы (1) устойчиво (асимптотически устойчиво) тогда и только тогда, когда устойчивым (асимптотически устойчивым) является нулевое решение x ≡ 0 системы в отклонениях (3).
Приведем формулировку устойчивого нулевого решения.
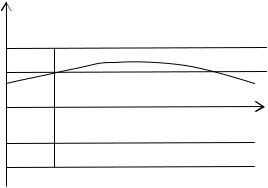
О п р е д е л е н и е 8 . Нулевое решение η = η(t) ≡ 0 (t ≥ 0) системы (3)
устойчиво, если для любого |
ε > 0 |
|
|
и каждого |
t0 ≥ 0 |
найдется такое число |
||||||||||||||||
δ = δ(ε, t0 )> 0 , что как только |
|
|
|
x(t0 ) |
|
|
|
< δ, |
то верно неравенство |
|
|
|
|
x(t) |
|
|
|
< ε |
при |
|||
|
|
|
|
|
|
|
|
|||||||||||||||
всех t ≥ t0 , где x = x(t) – произвольное решение системы (3) (см. рис. 1.5). |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Для нулевого решения системы |
||||||||||||
x |
|
|
|
|
|
|
|
|
|
(3) можно сформулировать определе- |
||||||||||||
|
|
|
|
|
|
|
|
|
ния равномерно, а также асимптоти- |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
ε |
|
|
|
|
x(t) |
|
|
|
чески устойчивого решений, области |
|||||||||||||
δ |
|
|
|
|
|
|
|
асимптотической |
устойчивости, |
|||||||||||||
|
|
|
|
|
|
|
|
|
асимптотически устойчивого в целом |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
0 |
t0 |
|
|
|
t |
|
|
|
и неустойчивого решений (читателю |
|||||||||||||
|
|
|
|
|
|
|
предлагается соответствующие опре- |
|||||||||||||||
–δ |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
деления выписать самостоятельно). |
|||||||||||||
–ε |
|
|
|
|
|
|
|
|
|
40. Примеры. |
|
|
|
|
|
|
|
|
|
|
||
Рис. 1.5. Иллюстрация к определению 8. |
1) Исследуем на устойчивость ре- |
|||||||||||||||||||||
шение |
линейного |
|
|
|
|
уравнения |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
y′ =1+ t − y , удовлетворяющее |
на- |
|||||||||||
чальному условию y(0)= 0 . Общее решение этого уравнения в форме Коши |
||||||||||||||||||||||
имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y(t;t0 , y0 )= y(t)= e−(t −t0 )(y0 + t et −t0 − t0 ) |
(t0 ≥ 0) . |
|
|||||||||||||||||||
Начальному условию y(0)= 0 |
отвечает решение |
y = η(t)= t . |
|
|
|
|
|
|
|
|
|
|
||||||||||
ГЛАВА 1. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ_______________________________________________23
Можно записать
|
|
|
|
|
y(t; t0 , y0 )− η(t) |
|
= |
|
y0 − t0 |
|
e |
−(t −t0 ) |
|
(η(t0 )= t0 ). |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Пусть |
|
y0 − η(t0 ) |
|
= |
|
y0 − t0 |
|
< δ. Тогда верно |
|
y(t;t0 , y0 )− η(t0 ) |
|
|
|
< δ e−(t −t0 ). |
||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Для устойчивости рассматриваемого решения нужно, чтобы выполнялось |
||||||||||||||||||||||||||||||||||
неравенство δ e−(t −t0 ) ≤ ε. Отсюда получаем |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
δ ≤ |
|
|
|
ε |
= ε et−t0 |
|
t ≥ t0 . |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
e |
−(t-t0 ) |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Следовательно, если взять δ = ε, |
то будет верно |
|
y0 − η(t0 ) |
|
< δ = ε, |
а значит и |
||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
неравенство |
|
y(t; t0 , y0 )− η(t) |
|
< ε e−(t−t0 ) |
≤ ε |
для всех t ≥ t0 . |
|
|||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||
Тем самым, устойчивость |
по |
|
|
Ляпунову |
|
установлена. А |
так как |
|||||||||||||||||||||||||||
e−(t −t0 ) → 0 , то решение η(t) асимптотически устойчиво в целом.
t→+∞
2) Исследуем на устойчивость нулевое решение уравнения
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
y′= |
r (t) |
|
|
|
|
|
|
|
|
sin |
t |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y , |
|
|
|
|
|
r(t) = |
t +1 + cos |
|
|
t |
|
|
( t ≥ 0 ). |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
r(t) |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
Имеем |
|
r(t) |
|
≤ |
|
sin2 t |
|
+ |
|
cos2 t |
|
≤1 +1 = 2 для всех |
|
t ≥ 0 . Нетрудно проверить, что |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
t +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r(t) |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
общее решение в форме Коши имеет вид y(t)= y |
|
|
|
. При | y |
|
|< δ для вы- |
||||||||||||||||||||||||||||||||||||||||||||
0 |
r(t0 ) |
0 |
||||||||||||||||||||||||||||||||||||||||||||||||
полнения устойчивости можно записать |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y(t)− 0 |
|
= |
|
y |
|
|
|
r(t) |
|
≤ |
2 |
|
y0 |
|
|
|
< |
|
|
2δ |
|
|
≤ ε. |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
ε r(t0 ) |
|
|
|
|
|
|
|
0 |
|
|
r(t0 ) |
|
r(t0 ) |
|
r(t0 ) |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Отсюда |
|
δ≤ |
|
. Значит, можно положить |
δ = |
ε |
r(t0 ) |
. При этом ясно, что |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||
величину δ невозможно выбрать не зависящей от |
|
|
t0 . Следовательно, нулевое |
|||||||||||||||||||||||||||||||||||||||||||||||
решение (неравномерно) устойчиво по Ляпунову. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
3) Перейдем к уравнению y′ =1 − y2 |
и исследует на устойчивость его реше- |
|||||||||||||||||||||||||||||||||||||||||||||||||
ние η(t) =1. |
|
Предварительно |
|
выполним |
замену |
|
|
y = x + η= x +1. Получим |
||||||||||||||||||||||||||||||||||||||||||
x′=1 −(x +1)2 |
|
или |
x′ = −x(x +2). Интегрируем полученное уравнение в от- |
|||||||||||||||||||||||||||||||||||||||||||||||
клонениях: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
