
- •Работа 1. Седиментационный анализ суспензий методом непрерывного взвешивания осадка.
- •Работа 20. Применение уравнения Фрейндлиха к адсорбции органических кислот на твердых адсорбентах.
- •Работа 32. Определение электрокинетического потенциала мембран методом электроосмоса.
- •Работа 39. Очистка коллоидных растворов и суспензий от электролитов методом электродиализа.
- •Работа 40а. Исследование зон коагуляции с помощью фотоэлектроколориметра.
- •Работа 48. Исследование процесса набухания твердых полимеров.
Работа 1. Седиментационный анализ суспензий методом непрерывного взвешивания осадка.
Этот метод основан на непосредственном определении увеличения веса осадка на какой-либо поверхности при седиментации. В данной задаче седиментационный анализ проводится при помощи торзионных весов – в ходе работы следует измерять увеличение массы осадка в чашечке, опущенной в оседающую суспензию и связанной кварцевой нитью с торзионными весами.
В начале опыта в литровый стакан до метки наливают дистиллированную воду, и, осторожно погрузив чашечку, отмечают показания торзионных весов (р0, мг), одновременно измеряя глубину погружения чашечки – разность между уровнем воды и дном чашечки (h, см). При измерениях надо тщательно следить за тем, чтобы чашечка не касалась стенок стакана. Для успешного проведения опыта оптимальные значения p0 = 70150 мг, h = 913 см (в приведенном ниже протоколе p0 = 99 мг, h = 12,2 см). После этих измерений чашечку аккуратно достают из воды и переносят в маленький стакан.
Затем готовят суспензию следующим образом: в фарфоровой ступке сначала растирают сухую навеску (10 г) исследуемого порошка (глина, стекло, диоксид титана), добавляя постепенно в ступку небольшое количество воды из стакана. Приготовленную однородную смесь переносят в стакан с оставшейся водой, смывая остатки смеси водой из этого же стакана – уровень суспензии должен достигать первоначальной отметки.
Перед опытом перемешивают полученную суспензию с помощью стеклянной палочки, на конце которой прикреплен резиновый диск. Движением стеклянной палочки вверх и вниз достигают равномерного распределения частиц суспензии по всему объему. Следует производить перемешивание, поставив стакан в положение, удобное для последующих измерений – под коромысло торзионных весов.
Сразу после прекращения перемешивания быстро, но осторожно опускают в стакан чашечку, подвешивая ее к весам. Одновременно с погружением чашечки включают секундомер и стараются сделать первое измерение не позднее 30 секунд от начала оседания частиц. Для этого рычагом передвигают стрелку влево до тех пор, пока указатель не будет находиться против черты равновесия. По мере накопления осадка на чашечке указатель равновесия смещается влево, и во время измерений его возвращают снова в равновесное положение.
Скорость процесса седиментации полидисперсной суспензии бывает наибольшей в начале опыта. Поэтому в начале опыта измерения проводят через каждые 20 секунд; по мере приближения к концу опыта время между измерениями постепенно увеличивают до 1015 минут. Опыт считается законченным, когда за 20 минут на чашечке оседает 12 мг, что обычно происходит по прошествии 2 часов.
Данные опыта заносят в таблицу 1.1.
Таблица 1.1.
|
Вес чашечки с осевшими на ней частицами, мг |
Вес частиц, осевших на чашечке p, мг |
Время от начала опыта t, сек |
1000/t, сек-1 |
|
125 |
26 |
19 |
52.6 |
|
142 |
43 |
49 |
20.4 |
|
159 |
60 |
101 |
9.9 |
|
166 |
67 |
129 |
7.8 |
|
172 |
73 |
175 |
5.7 |
|
178 |
79 |
196 |
5.1 |
|
184 |
85 |
230 |
4.3 |
|
190 |
91 |
285 |
3.5 |
|
195 |
96 |
358 |
2.8 |
|
197 |
98 |
402 |
2.5 |
|
202 |
103 |
439 |
2.3 |
|
203 |
104 |
476 |
2.1 |
|
204 |
105 |
496 |
2.0 |
|
205 |
106 |
524 |
1.9 |
|
206 |
107 |
557 |
1.8 |
|
212 |
113 |
620 |
1.6 |
|
214 |
115 |
672 |
1.5 |
|
217 |
118 |
745 |
1.3 |
|
218 |
119 |
813 |
1.2 |
|
224 |
125 |
955 |
1.0 |
|
229 |
130 |
1141 |
0.9 |
|
230 |
131 |
1283 |
0.8 |
|
235 |
136 |
1499 |
0.7 |
|
239 |
140 |
1801 |
0.6 |
|
242 |
143 |
2116 |
0.5 |
|
245 |
146 |
2443 |
0.4 |
|
247 |
148 |
2747 |
0.35 |
|
252 |
153 |
3295 |
0.3 |
|
253 |
154 |
3931 |
0.25 |
|
253 |
154 |
5115 |
0.2 |
|
253 |
154 |
5417 |
0.18 |
По
полученным данным строят седиментационную
кривую (рис. 1.1), откладывая по оси ординат
вес осевших на чашечке частиц
p,
мг; а по оси абсцисс – время от начала
опыта – t,
сек. При построении седиментационных
кривых рекомендуемый формат миллиметровой
бумаги А3 или А4; если необходимо, начальный
участок можно построить в более крупном
масштабе. Для нахождения предела
седиментации строят начальный участок
зависимости p
= f(1000/t)
и экстраполируют полученную кривую на
ось ординат (рис. 1.2). Точка пересечения
соответствует величине pmax,
т.к. при
![]()
![]() .
.
Из полученной седиментационной кривой (рис. 1.1) можно рассчитать процентное соотношение отдельных фракций частиц в суспензии. Для этого выбирают несколько точек (710) на кривой и проводят касательные к каждой точке. Следует обратить внимание на построение ординат к кривой седиментации для тех случаев, когда кривая и касательная на некотором участке полностью сливаются, т.е. когда некоторые участки седиментационной кривой являются прямолинейными, что наблюдается при оседании частиц с определенным радиусом. Для вычисления этого радиуса следует взять максимальное время, соответствующее точке отрыва касательной от кривой.

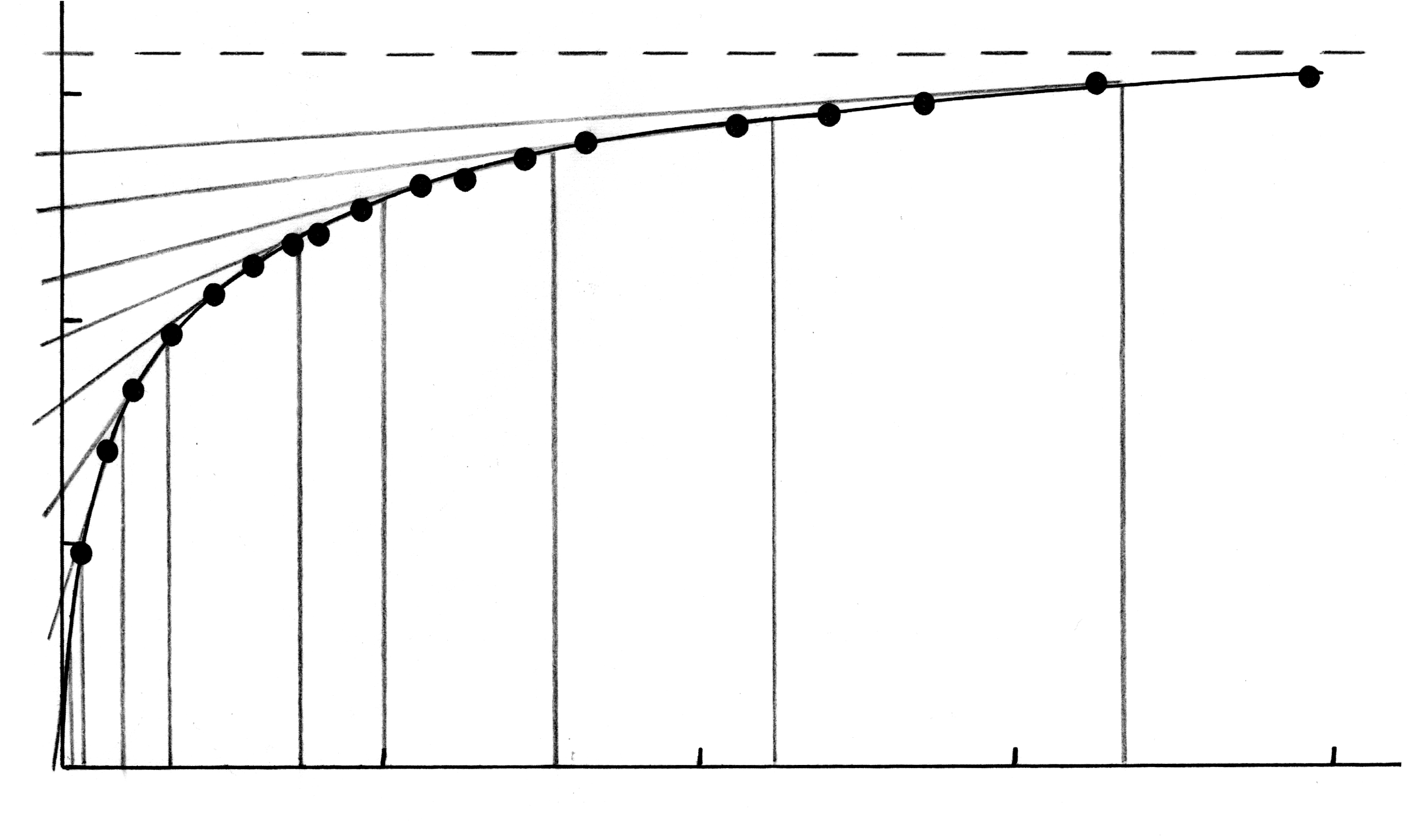
Рис. 1.1. Седиментационная кривая.
Каждая
касательная к кривой седиментации
отсекает от оси ординат отрезок, равный
весу частиц, полностью осевших к данному
моменту времени. Тогда как ординаты,
проведенные из точек касания, отсекают
на оси абсцисс отрезки, соответствующие
времени полного оседания различных
фракций. Например, касательной, проходящей
через точку А (рис. 1.1), соответствует
вес частиц pА
и время оседания tА.
Для каждого времени оседания можно
рассчитать эквивалентный радиус частиц
по формуле:
![]() =
=
![]() ,
где
,
где
![]() – скорость оседания частиц, см/с;
и
– скорость оседания частиц, см/с;
и
![]()
вязкость и плотность воды, равные,
соответственно, 0.01 пз и 1 г/см3;
g
– ускорение свободного падения, равное
981 см/с2;
d
– плотность частицы диспергированного
вещества, г/см3.
При выражении
радиусов частиц в микронах (мкм),
вязкость и плотность воды, равные,
соответственно, 0.01 пз и 1 г/см3;
g
– ускорение свободного падения, равное
981 см/с2;
d
– плотность частицы диспергированного
вещества, г/см3.
При выражении
радиусов частиц в микронах (мкм),
![]() .
В случае дисперсионного анализа суспензий
стекла d
= 2.5 г/см3
и
.
В случае дисперсионного анализа суспензий
стекла d
= 2.5 г/см3
и
![]() .
.
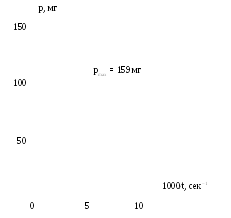
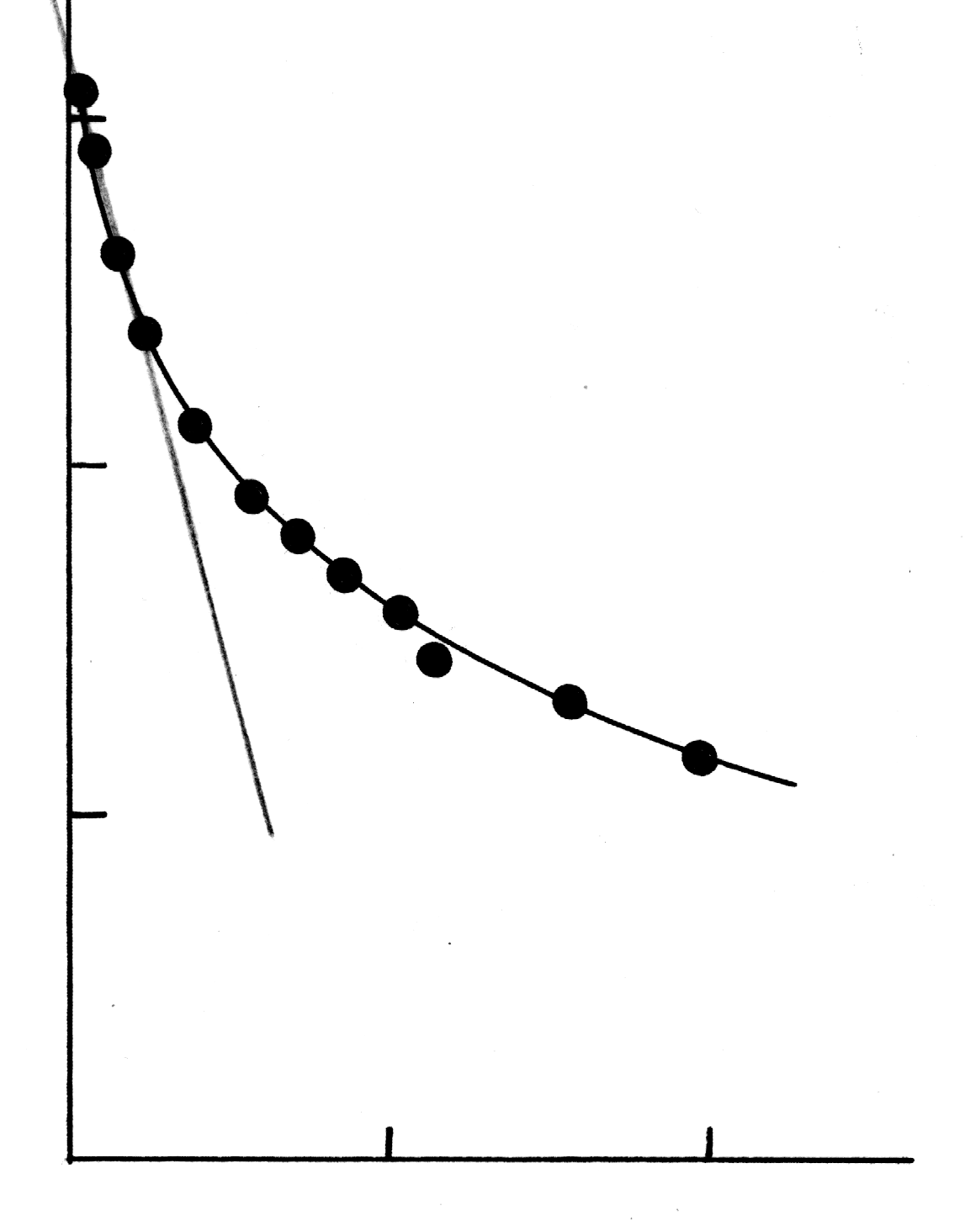
Рис. 1.2. Определение предела седиментации.
После вычисления эквивалентных радиусов измеряют длины отрезков ординаты между касательными (в мм) и выражают их в процентах от общей длины ординаты (от начала координат до предела седиментации; в нашем случае ордината равна 159 мм). Отрезок ординаты от начала координат до точки пересечения первой касательной (p1), отнесенный к общей длине ординаты, дает процентное содержание частиц в интервале между максимальным эквивалентным радиусом (в нашем случае 40 мкм) и наибольшим, определенным по седиментационной кривой. Из величин отдельных отрезков между касательными (см. рис. 1.1) вычисляют процентное содержание частиц фракций между соответствующими им эквивалентными радиусами. Отрезок от предела седиментации до ближайшей к нему касательной (p9) выражает относительное содержание частиц меньше определенного из седиментационной кривой наименьшего эквивалентного радиуса.
Полученные данные записывают в таблицу 1.2.
Таблица 1.2.
-
Время оседания t, сек
Радиус частиц r, мкм
Интервалы размеров частиц отдельных фракций, мк
Длина отрез-ков между касательными, мм
Содержание фракций в системе, %
3343
3.3
< 3.3
21
13.2
2243
4.1
3.3 – 4.1
13
8.2
1529
4.9
4.1 – 4.9
16
10.1
1014
6.1
4.9 – 6.1
13
8.2
743
7.1
6.1 – 7.1
15
9.4
329
10.6
7.1 – 10.6
19
11.9
186
14.2
10.6 – 14.2
25
15.7
57
25.6
14.2 – 25.6
19
11.9
29
35.9
25.6 – 35.9
10
6.3
35.9 – 40.0
8
5.1
Всего:
159
100
На основании данных таблицы строят суммарную кривую распределения (рис. 1.3): откладывают по оси ординат суммарное процентное содержание фракций Q, начиная с самых мелких частиц; по оси абсцисс – радиусы частиц, соответствующие большему значению радиуса данной фракции. Например, если в исследуемом порошке наиболее мелкая фракция содержит частицы с эквивалентными радиусами < 3.3 мкм и относительное количество ее в дисперсной системе 13.2%, то по оси ординат откладывают 13.2%, а по оси абсцисс 3.3 мкм. Следующая фракция находится в пределах 3.34.1 мкм и относительное ее количество 8.2%, тогда по оси абсцисс откладывают величину 4.1 мкм, а по оси ординат откладывают суммарное процентное содержание обеих фракций, т.е. 13.2% + 8.2% = 21.4%.


Рис. 1.3. Интегральная кривая распределения частиц по размеру.
Полученный график называется интегральной кривой распределения. Любая точка этой кривой показывает процентное содержание в системе частиц с меньшими эквивалентными радиусами, чем соответствующий ей по оси абсцисс. Следует отметить, что на этом графике отложены не целочисленные значения радиусов частиц, а величины радиусов, соответствующие тем временам седиментации, которые мы выбрали при проведении касательных к седиментационной кривой. При переходе от интегральной к дифференциальной кривой распределения ось абсцисс на рис. 1.3 разбивают на равные интервалы радиусов (обычно этот интервал выбирают в 25 мкм) и находят величины приращения процентного содержания частиц Q/r для каждого интервала. Найденные величины записывают в таблицу 1.3.
Таблица 1.3.
-
r, мкм
Q, %
Q, %
Q/r
5
33
33
6.6
10
59
26
5.2
15
78
19
3.8
20
84
6
1.2
25
89
5
1.0
30
92
3
0.6
35
95
3
0.6
40
100
5
1.0
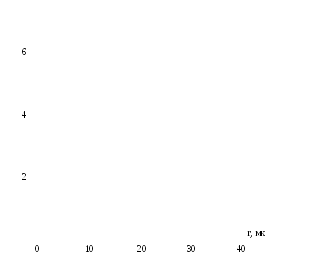

Рис. 1.4. Дифференциальная кривая распределения частиц по размеру.
По данным таблицы 1.3 строят дифференциальную кривую распределения (рис. 1.4), откладывая по оси ординат Q/r, а по оси абсцисс радиусы. Например, Q/r в интервале радиусов от 0 до 5 мкм равно 6.6. Графически это показано на рис. 1.4 первым прямоугольником. Второй прямоугольник строят в интервале радиусов от 5 до 10 мкм и так до максимального радиуса частиц. Соединив середины прямоугольников, получают плавную кривую с одним максимумом, соответствующим наиболее вероятному размеру частиц основной фракции. Следует отметить, что форма полученной дифференциальной кривой, в зависимости от характера дисперсности исследуемой системы, может быть различной; например, у полидисперсной системы вполне может оказаться дифференциальная кривая с двумя максимумами.
Работа 16. Измерение поверхностного натяжения методом наибольшего давления пузырьков.
Работа 19. Исследование связи между поверхностным натяжением и адсорбцией.
Перед началом работы измерительный капилляр, сосудик, рабочие колбы (5 на 100 мл – для первого потока; 6 на 100 мл и 6 на 50 мл для второго) и пипетки (на 50 мл; на 50 и 25 мл для разных потоков, соответственно) тщательно промывают хромовой смесью, водопроводной водой и дистиллированной водой. Делают это следующим образом.
В сосудик до половины наливают хромовой смеси (57 мл), опускают туда капилляр так, чтобы шарик капилляра был полностью погружен в жидкость, и оставляют стоять, а в это время моют колбы. В одну из колб наливают небольшое количество хромовой смеси. Этим объемом ополаскивают внутри все колбы, переливая хромовую смесь из одной колбы в другую, и в конце сливая ее в керамический стакан для слива. Из этого стакана в пипетку грушей засасывают хромовую смесь так, чтобы уровень жидкости на 2 см был выше метки, и осторожно через носик пипетки выливают хромовую смесь назад в керамический стакан. После этого выливают из сосудика хромовую смесь в стакан для слива, а из капилляра выдувают ее туда же при помощи груши.
Затем всю посуду промывают 20 раз водопроводной водой. Пипетки, сосудик и колбы ополаскивают дистиллированной водой и одну колбу на 100 мл – для задачи – ставят в сушильный шкаф. Капилляр промывают от хромовой смеси сразу дистиллированной водой с помощью водоструйного насоса. Для этого шланг от насоса надевают на капилляр, погружают его в стакан с дистиллятом и просасывают через капилляр 500 мл воды. Следует отметить, что малейшие загрязнения (например, прикосновение рукой) частей капилляра и сосудика, соприкасающихся с изучаемой жидкостью, приводят к неправильным результатам.

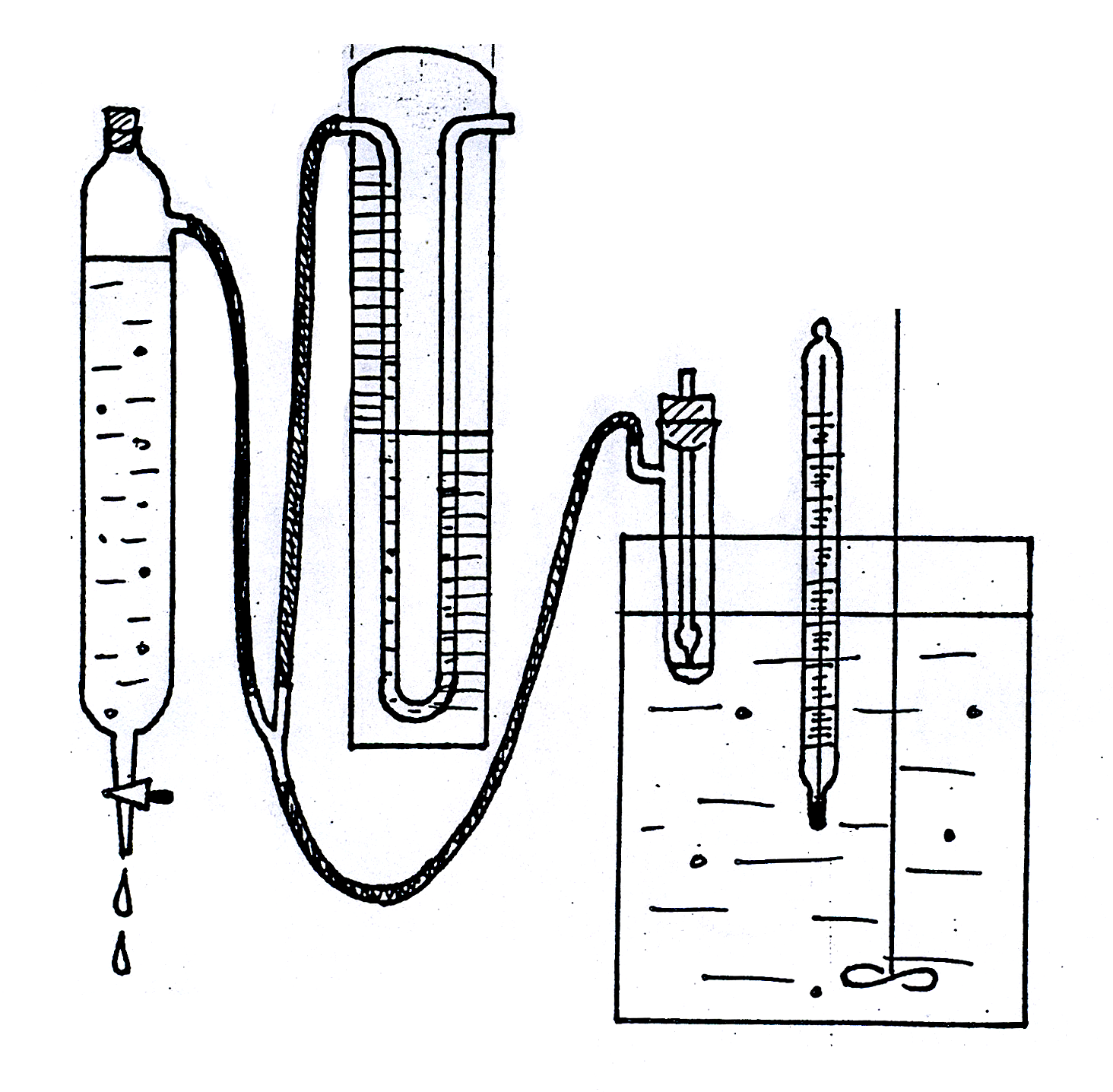
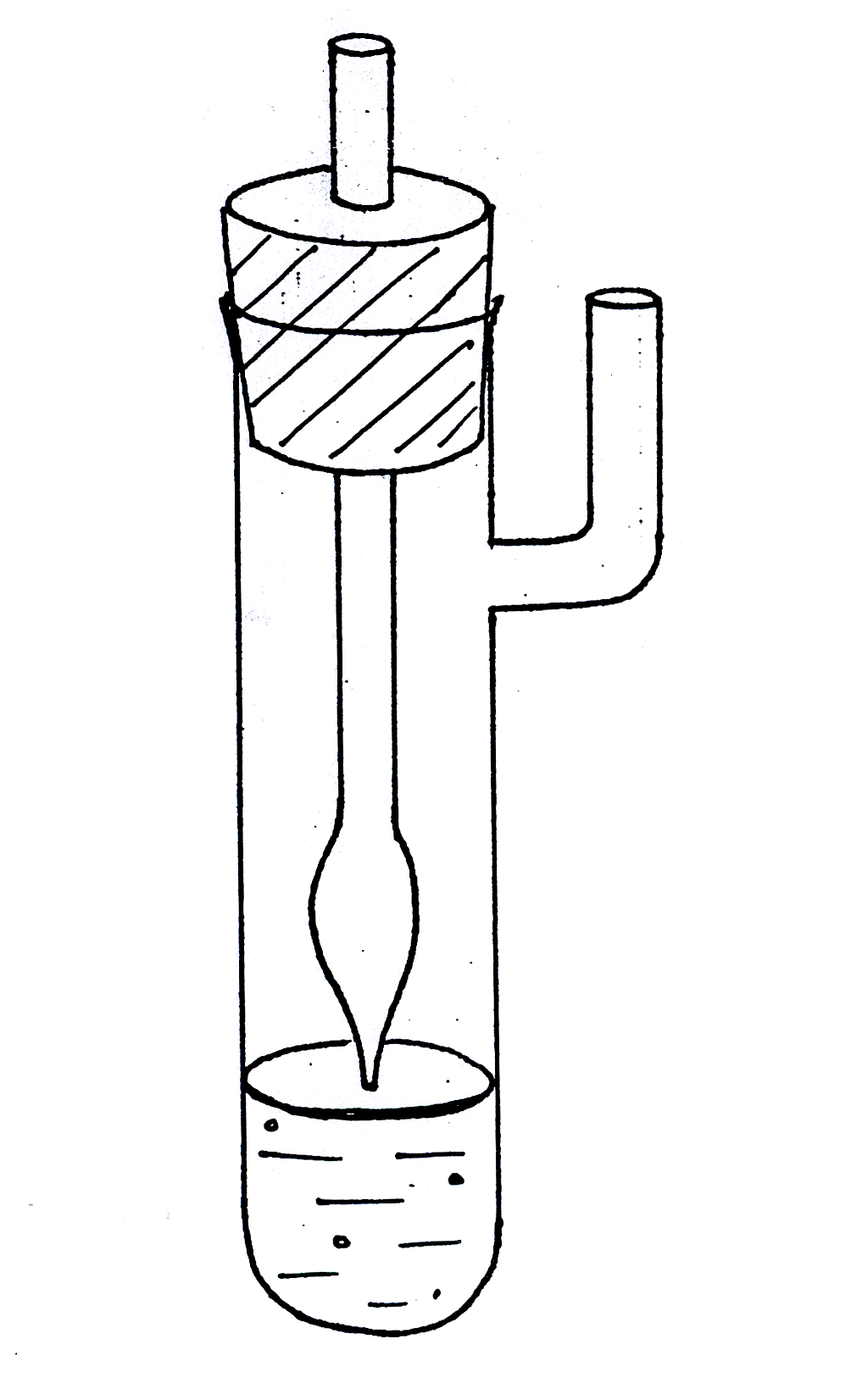
Рис. 1619.1, 1619.1а. Установка для измерения поверхностного натяжения методом
наибольшего давления пузырьков.
Для измерения поверхностного натяжения методом наибольшего давления пузырьков целесообразно пользоваться прибором, разработанным академиком П.А. Ребиндером (рис. 1619.1). Исследуемую жидкость наливают в термостатированный сосудик (1) с боковым отростком, в который опускают капилляр (2) таким образом, чтобы он только касался поверхности жидкости, но не был погружен в нее (см. рис. 1619.1а). Боковой отросток соединяется с аспиратором – устройством для создания разрежения в сосудике – герметичным стеклянным цилиндром, разрежение воздуха в котором создается за счет вытекающей из него воды; при этом происходит просасывание воздуха через кончик капилляра в жидкость с образованием пузырьков. С системой соединен водяной манометр (4), позволяющий определять максимальное давление в пузырьке по разности уровней воды в обоих коленах манометра (h = h1 + h2).
Ознакомившись с устройством прибора, определяют константу капилляра K по дистиллированной воде. Для этого наливают в сосуд немного воды и погружают туда капилляр так, чтобы он только касался поверхности жидкости, но не был погружен в нее (см. рис. 1619.1а). При этом пробка с капилляром должна быть плотно вставлена в сосудик.
Далее сосуд помещают в термостат и соединяют с аспиратором, внимательно следя за тем, чтобы уровень воды в аспираторе находился между двумя метками, а в соединительных шлангах не было ни капли воды. Во время измерений аспиратор должен быть плотно закрыт пробкой; воду в аспиратор следует доливать только при помощи воронки, поскольку наличие воды в соединительных шлангах приводит к неправильным показаниям манометра. Скорость вытекания воды из аспиратора регулируют таким образом, чтобы число пузырьков воздуха, проходящих через капилляр, не превышало 58 в минуту; при большей скорости равновесные условия не достигаются, и результаты измерений оказываются неправильными.
Отсчет
наибольшей величины h,
отвечающей максимальному давлению в
пузырьке воздуха, производят при помощи
лупы по зеркальной шкале манометра
таким образом, чтобы отражение глаза
наблюдателя в зеркале было на уровне
мениска. Записывают показания обоих
колен манометра и берут их сумму: h
= h1
+ h2.
Затем вычисляют константу капилляра
![]() ,
причем выполняют эти измерения три
раза, каждый раз заново заполняя сосудик
водой. В нашем случае результаты всех
трех измерений совпали, и единственная
константа капилляра оказалась равна
1.373. Вычисленные константы (с хорошей
сходимостью) показывают лаборантам. От
того, насколько качественно определена
константа капилляра, зависит успех
дальнейшей работы.
,
причем выполняют эти измерения три
раза, каждый раз заново заполняя сосудик
водой. В нашем случае результаты всех
трех измерений совпали, и единственная
константа капилляра оказалась равна
1.373. Вычисленные константы (с хорошей
сходимостью) показывают лаборантам. От
того, насколько качественно определена
константа капилляра, зависит успех
дальнейшей работы.
Далее в 4 пронумерованные колбы на 100 мл (№№ 25) (5 – для второго потока (№№ 26)) пипеткой наливают по 50 мл дистиллированной воды. После этого в сухую остывшую колбу на 100 мл (№ 1) – которую Вы после мытья поставили в сушильный шкаф – получают задачу, водный раствор ПАВ. Затем отбирают пипеткой 50 мл исходного раствора из колбы с задачей и добавляют его в колбу с водой (№ 2), выдувая грушей содержимое из носика пипетки. Перемешивают полученный раствор, продувая грушей воздух через пипетку, носик которой погружен в жидкость. Далее отбирают 50 мл полученного раствора этой же пипеткой и добавляют в следующую колбу с водой (№ 3). Хорошо перемешивают полученный раствор, отбирают 50 мл полученного раствора и так далее до тех пор, пока не получают 5 растворов (6 – для второго потока), включая исходный.
Таким образом, в результате последовательного разбавления получили колбы с растворами, разбавленными в 2, 4, 8, 16 (32 – для второго потока) раза, соответственно. Измерения поверхностного натяжения начинают с самого разбавленного раствора, которому соответствует колба с наибольшим номером (№ 5 – для первого потока и № 6 – для второго). Перед измерением сосуд с капилляром тщательно промывают исследуемым раствором – в сосудик наливается жидкость, с помощью груши ее засасывают в шарик капилляра и выдувают в раковину. Эту процедуру повторяют 1215 раз.
После
чего наливают в сосуд немного исследуемого
раствора и погружают туда капилляр так,
чтобы он только касался поверхности
жидкости, но не был погружен в нее (см.
рис. 1619.1а).
Измеряют наибольшую величину h
для исследуемого раствора аналогично
измерениям при определении константы
капилляра
снимают показания обоих колен манометра
и берут их сумму: h
= h1
+ h2,
только измерения для раствора проводят
один раз. Затем вычисляют значения
поверхностного натяжения исследуемого
раствора 5(6)
со всеми получившимися константами
![]() .
Каждое значение
обязательно проверяется в лаборантской;
следующий раствор, с большей концентрацией
ПАВ, измеряется только после того, как
было принято значение
для предыдущего раствора.
.
Каждое значение
обязательно проверяется в лаборантской;
следующий раствор, с большей концентрацией
ПАВ, измеряется только после того, как
было принято значение
для предыдущего раствора.
Закончив измерения серии растворов, студентам первого потока и бакалаврам необходимо вылить остатки рабочих растворов в раковину, сполоснуть колбы водопроводной водой, залить сосудик с капилляром дистиллированной водой и получить в лаборантской данные об исследуемом ПАВ – исходную концентрацию C, молекулярную массу М, плотность d (в нашем случае эти величины равны 0.6 М, 74.08 и 0.8 г/мл, соответственно).
Студенты, обучающиеся на втором потоке, продолжают работу, изучая адсорбцию на границе раздела раствор ПАВ – твердый адсорбент (активированный уголь). Для этого в каждую из шести колб на 50 мл насыпают по 1 г адсорбента – активированного угля; при этом необходимое количество угля отмеряют пробиркой, насыпая уголь до метки. Затем пипеткой на 25 мл отбирают самый разбавленный раствор и переносят его в одну из колб с углем. Ставят на колбе тот же номер (№ 6), что и на колбе, из которой был взят раствор. Переходят к более концентрированному раствору и повторяют вышеуказанную операцию. Таким образом заливают все колбы с углем, плотно закрывают пробками, встряхивают и оставляют в шкафу, на подписанном месте, до следующего занятия. Вместе с колбами оставляют сосудик с капилляром, предварительно промытый дистиллированной водой и полностью, до верха, заполненный ею.
Через неделю необходимо измерить поверхностное натяжение растворов ПАВ после адсорбции, начиная с самого разбавленного раствора (колба № 6 на 50 мл). Полученные данные по каждому раствору обязательно проверяются в лаборантской. Если на первом занятии Вы не успели закончить измерения поверхностного натяжения растворов ПАВ до адсорбции, то схема измерения будет следующая: самый разбавленный раствор 1/32 (колба № 6 на 50 мл) после адсорбции, самый разбавленный раствор 1/32 (колба № 6 на 100 мл) до адсорбции, 1/16 (колба № 5 на 50 мл) после адсорбции, 1/16 (колба № 5 на 100 мл) до адсорбции, 1/8 (колба № 4 на 50 мл) после адсорбции, 1/8 (колба № 4 на 100 мл) до адсорбции, 1/4 (колба № 3 на 50 мл) после адсорбции, 1/4 (колба № 3 на 100 мл) до адсорбции, 1/2 (колба № 2 на 50 мл) после адсорбции, 1/2 (колба № 2 на 100 мл) до адсорбции, исходный раствор (колба № 1 на 50 мл) после адсорбции, исходный раствор (колба № 1 на 100 мл) до адсорбции. Таким образом, при переходе к следующему раствору, концентрация ПАВ будет расти, а значения уменьшаться.
Закончив измерения, необходимо вылить остатки рабочих растворов вместе с углем в соответствующую емкость, сполоснуть колбы водопроводной водой, залить сосудик с капилляром дистиллированной водой и получить в лаборантской данные об исследуемом ПАВ – исходную концентрацию С, молекулярную массу М, плотность d (в нашем случае эти величины равны 0.6 М, 74.08 и 0.8 г/мл, соответственно).
Полученные экспериментальные данные
и результаты вычислений заносят в
таблицу 1619.1. Величины
адсорбции рассчитывают по формуле
![]() ,
где
,
где
![]() ,
=
i+1
– i,
C
= Ci+1
– Ci.
Эти данные используют для построения
зависимости поверхностного натяжения
от концентрации ПАВ в растворе (рис.
1619.2) и изотермы
адсорбции (рис. 1619.3),
откладывая по оси абсцисс значения
концентрации С (М) и Сср (М), а по
оси ординат – величины поверхностного
натяжения
(эрг/см2) и Г (моль/см2),
соответственно.
,
=
i+1
– i,
C
= Ci+1
– Ci.
Эти данные используют для построения
зависимости поверхностного натяжения
от концентрации ПАВ в растворе (рис.
1619.2) и изотермы
адсорбции (рис. 1619.3),
откладывая по оси абсцисс значения
концентрации С (М) и Сср (М), а по
оси ординат – величины поверхностного
натяжения
(эрг/см2) и Г (моль/см2),
соответственно.
Таблица 1619.1.
|
С, М |
h, мм |
, эрг/см2 (мН/м) |
С, М |
, эрг/см2 (мН/м) |
|
Cср, М |
|
|
|
0 |
53 |
72.75 |
|
|
|
|
|
|
|
0.019 |
50 |
68.65 |
0.019 |
4.1 |
218.7 |
0.009 |
0.83 |
11.3 |
|
0.038 |
49.5 |
65.0 |
0.019 |
3.65 |
194.7 |
0.028 |
2.21 |
12.7 |
|
0.075 |
44 |
59.27 |
0.037 |
5.73 |
152.8 |
0.056 |
3.47 |
16.2 |
|
0.15 |
38 |
52.0 |
0.075 |
7.27 |
96.9 |
0.113 |
4.40 |
25.5 |
|
0.3 |
31.5 |
43.25 |
0.15 |
8.75 |
58.3 |
0.225 |
5.30 |
42.5 |
|
0.6 |
26 |
34.1 |
0.3 |
9.15 |
30.5 |
0.450 |
5.54 |
81.2 |


Рис. 1619.2. Изотерма поверхностного натяжения.
Для нахождения величины предельной
адсорбции
![]() и константы k уравнения
адсорбции Лэнгмюра, преобразуют уравнение
и константы k уравнения
адсорбции Лэнгмюра, преобразуют уравнение
![]() так, чтобы получить уравнение прямой,
деля С на обе части уравнения. После
сокращения получают уравнение прямой,
не проходящей через начало координат
так, чтобы получить уравнение прямой,
деля С на обе части уравнения. После
сокращения получают уравнение прямой,
не проходящей через начало координат
![]() .
.

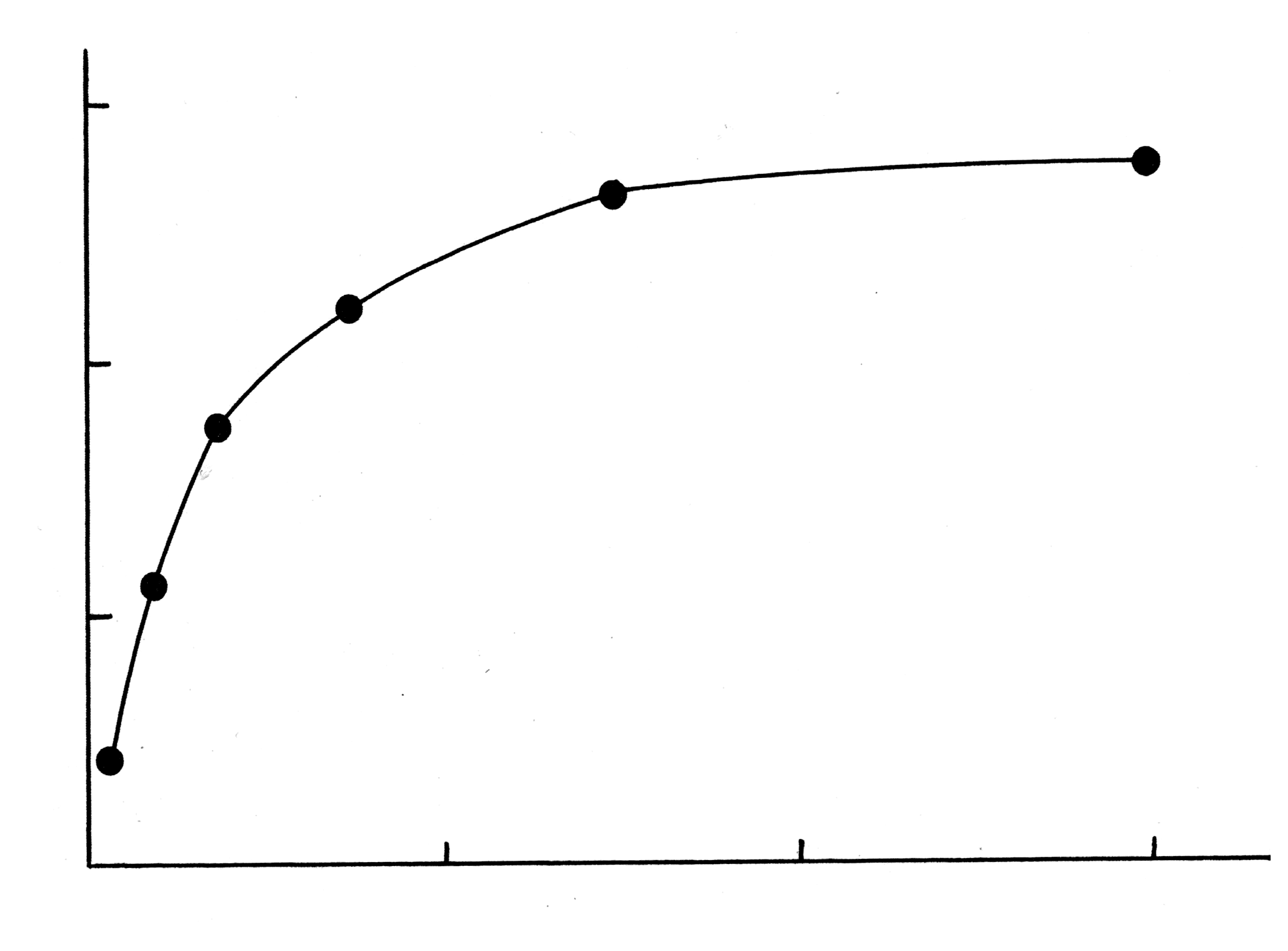
Рис. 1619.3. Изотерма адсорбции Лэнгмюра.
Величину
![]() определяют по углу наклона прямой:
определяют по углу наклона прямой:
![]() .
Построив график
.
Построив график
![]() (рис.
1619.4), находят
соответствующие катеты и вычисляют
(рис.
1619.4), находят
соответствующие катеты и вычисляют
![]() .
По отрезку, отсекаемому прямой на оси
ординат, можно найти константу k.
В нашем случае
.
По отрезку, отсекаемому прямой на оси
ординат, можно найти константу k.
В нашем случае
![]() моль/см2
и
моль/см2
и
![]() ,
откуда
,
откуда
![]() .
При этом уравнение адсорбции Лэнгмюра
имеет вид
.
При этом уравнение адсорбции Лэнгмюра
имеет вид
![]() .
.


Рис.1619.4. Определение константы уравнения адсорбции Лэнгмюра.
Далее, зная величину предельной адсорбции
![]() ,
можно вычислить площадь А, занимаемую
одной молекулой в поверхностном слое,
и толщину поверхностного слоя .
В нашем случае
,
можно вычислить площадь А, занимаемую
одной молекулой в поверхностном слое,
и толщину поверхностного слоя .
В нашем случае
![]() =
2.7.1015
см2 и
=
2.7.1015
см2 и
![]() см.
см.
Во второй части работы при изучении
адсорбции ПАВ на поверхности твердого
адсорбента для всех приготовленных
растворов были измерены величины
поверхностного натяжения x
после сорбции. Значения Cx,
концентрацию ПАВ после адсорбции,
находят графически из зависимости
поверхностного натяжения от концентрации
(см. рис. 1619.2), опуская
перпендикуляр из точки, соответствующей
x,
на ось абсцисс. По формуле
![]() ,
где V – объем раствора
(0.025 л) и m – масса адсорбента
(1 г), находят величину адсорбции,
отнесенную к единице массы адсорбента.
Полученные экспериментальные данные
и результаты вычислений заносят в
таблицу 1619.2.
,
где V – объем раствора
(0.025 л) и m – масса адсорбента
(1 г), находят величину адсорбции,
отнесенную к единице массы адсорбента.
Полученные экспериментальные данные
и результаты вычислений заносят в
таблицу 1619.2.
Таблица 1619.2.
-
С, М
, эрг/см2 (мН/м)
x, эрг/см2 (мН/м)
Cx, М
С – Сx, М
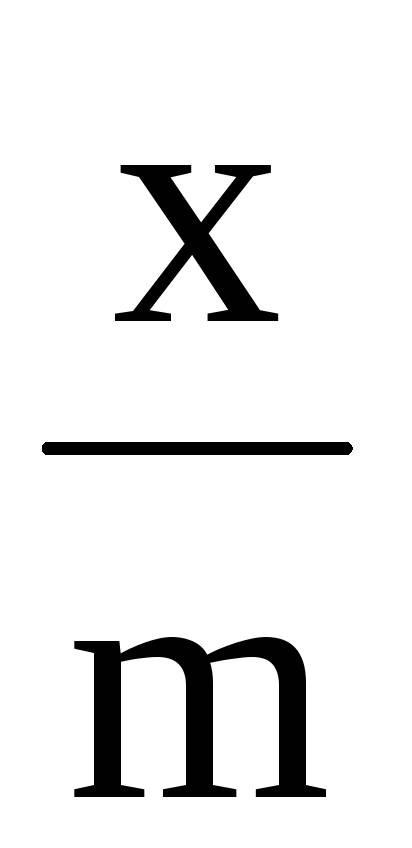 ,
ммоль/г
,
ммоль/г0.6
34.1
37.7
0.45
0.15
3.75
0.3
43.25
47.34
0.19
0.11
2.75
0.15
52.0
59.04
0.08
0.07
1.75
0.075
59.27
64.0
0.04
0.035
0.88
0.038
65.0
68.7
0.02
0.018
0.45
0.019
68.65
71.34
0.01
0.009
0.22
Эти
данные используют для построения
изотермы адсорбции на границе раздела
твердое тело – жидкость, откладывая по
оси абсцисс значения концентрации Сx
(М), а по оси ординат – количество
вещества, адсорбированное одним граммом
угля
![]() (ммоль/г). Подобная зависимость приведена
на рис. 1619.5.
(ммоль/г). Подобная зависимость приведена
на рис. 1619.5.

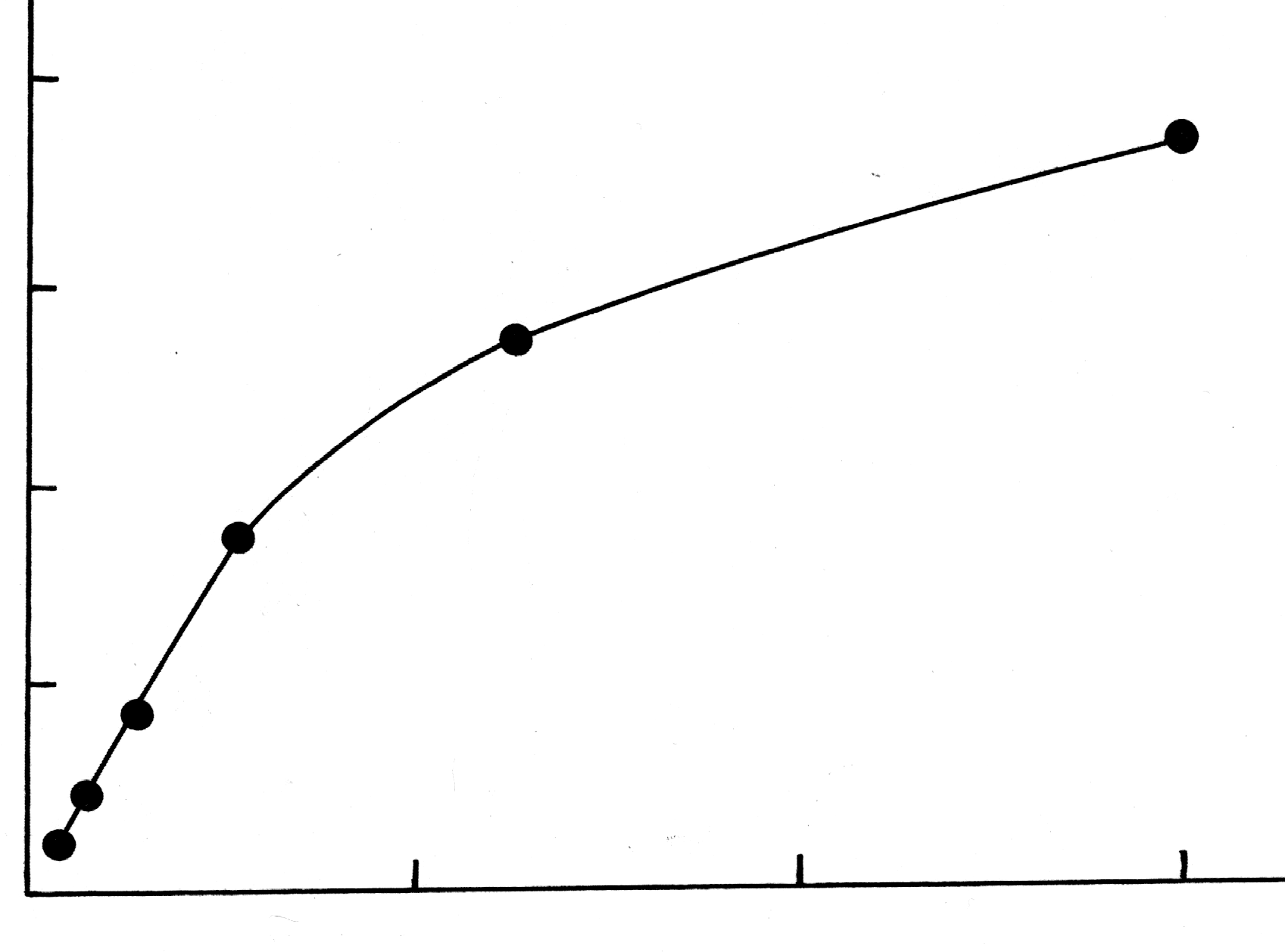
Рис.1619.5. Изотерма адсорбции на границе раздела твердое тело – жидкость.
Если
предел адсорбции не достигнут, что может
быть в случае высокопористых адсорбентов
или при малой растворимости адсорбируемого
вещества, в качестве предельного
![]() принимают наибольшее значение
принимают наибольшее значение
![]() .
Далее вычисляют величину удельной
поверхности адсорбента S
(см2/г)
– суммарную площадь поверхности,
отнесенную к единице массы адсорбента.
В нашем случае
.
Далее вычисляют величину удельной
поверхности адсорбента S
(см2/г)
– суммарную площадь поверхности,
отнесенную к единице массы адсорбента.
В нашем случае
![]() .
.
