formal_language_theory / lectures / unit_11
.pdf
Если S
lm
x , то (xy, S$, ) 
(y, $, )
Посмотрим, как будет действовать анализатор, начиная с конфигурации (xy, S$, ).
Очевидно, что аванцепочка u FIRST1G(xy) FIRST1G(x )
FIRST1G(x ) FIRST1G(x FOLLOW1G (S)),
и, следовательно, M (S, u) = (x , i). Поэтому
(xy, S$, ) 
(xy, x $, i) 
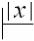(y, $, i),
причём последний переход реализуется посредством pop-движений.
База доказана.
101
Если S
lm
x , то (xy, S$, ) 
(y, $, )
Индукционная гипотеза. Предположим,
что утверждение выполняется для всех l n
(n 1).
Индукционный переход. Докажем утверж-
дение для l = n + 1.
Пусть |
имеется левосторонний вывод |
|
длиной n + 1: |
|
|
S |
|
( i ) |
|
x’ ’ = x’A x’ = x . |
|
|
|
|
Здесь |
lm |
lm |
= |
’i, ’ = A , = z , где z VT*, |
|
x = x’z, A VN, , V*.
102
Если S
lm
x , то (xy, S$, ) 
(y, $, )
На последнем шаге вывода применялось правило A — i-е правило из множества
правил P. |
|
Согласно алгоритму 2.1 |
|
M (A, a) = ( , i) |
(2.1) |
для всех a FIRST1G ( FOLLOW1G ( A)).
Посмотрим, как будет действовать анализатор из своей начальной конфигура-
ции (xy, S$, ) = (x’zy, S$, ) = (x’y’, S$, ), где y’ = zy.
103
|
|
|
|
|
|
|
|
(y, $, ) |
|
|
|
|
|
||
|
Если S x , то (xy, S$, ) |
|
|
|
|
|
|
||||||||
|
lm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Применим к имеющемуся выводу S |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lm |
индукционную |
гипотезу с |
цепочкой |
|||||||||||||
поскольку |
|
|
|
|
|
|
|
|
|
|
|
||||
|
FIRST |
G |
|
|
|
|
G |
(zy) FIRST |
G |
(z ) |
|||||
|
|
( y ) FIRST |
|
|
|||||||||||
1 |
|
|
|
1 |
|
|
|
1 |
|
|
|
||||
|
FIRST |
G |
( ) FIRST |
G |
( A ) FIRST |
G |
|
||||||||
|
|
|
|
( ). |
|||||||||||
|
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|||
x’ ’ y’,
Как следствие получаем
(xy, S$, ) = (x′zy, S$, ) =
= (x′y′, S$, )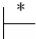 
(y′, ′$, ′) = (zy, A $, ′).
104
Если S
lm
x , то (xy, S$, ) 
(y, $, )
Вычислим аванцепочку от zy:
G |
|
G |
(z ) |
|
|
|
u FIRST |
(zy) FIRST |
|
|
|||
1 |
|
1 |
|
|
|
|
G |
G |
( FOLLOW |
G |
( A)), |
||
FIRST |
|
( ) FIRST |
|
|
||
1 |
|
1 |
|
1 |
|
|
а для таких аванцепочек, как показывает равенство (2.1), M (A, u) = ( , i).
Поэтому следующее движение и завершающие pop-движения продолжают процесс таким образом:
(zy, A $, ’) 
(zy, $, ’i) = = (zy, z $, ’i)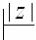 
(y, $, ).
Утверждение (I) доказано. |
105 |
Если (xy, S$, ) 
(y, $, ), то S
lm
x
II. Докажем теперь, что если анализатор совершает переход вида
(xy, S$, ) 
(y, $, )
для любой цепочки y *, такой, что
|
|
G |
|
|
|
FIRST |
|
|
|
1 |
|
|
x , где x |
||
то S |
|
||
lm |
|||
|
|
открытая часть формы x .
( y) FIRST |
G |
( ), |
|
1 |
|||
|
|
— закрытая часть, а — данной сентенциальной
Индукция по l = .
106
Если (xy, S$, ) 
(y, $, ), то S
lm
x
База. Пусть l = 1, т. е. = i.
Имеем (xy, S $, )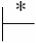 
(y, $, i). Анализатор пишет на выходную ленту номер правила только при движении типа 1, а оно совершается только при наличии нетерминала на вершине магазина.
Следовательно, это — первое движение, и только оно, пишет номер i на выход.
107
Если (xy, S$, ) 
(y, $, ), то S
lm
x
Поэтому фактически имеем
(xy, S$, ) 
(xy, $, i) =
= (xy, x $, i) 
(y, $, i),
причём все остальные движения — это popдвижения. Очевидно, что только при = x достижима последняя конфигурация.
Первое движение обеспечивается элементом
таблицы M(S, u) = ( , i), где |
|
G |
(xy), |
1 |
|||
|
u FIRST |
|
|
а это подразумевает существование правила
S = x под номером i. А тогда S ( i ) x .
lm
108
Если (xy, S$, ) 
(y, $, ), то S
lm
x
Индукционная гипотеза. Предположим,
что утверждение выполняется для всех l n
(n 1).
Индукционный переход. Докажем утверж-
дение для l = n + 1.
Пусть (xy, S$, ) = (x’y’, S$, ) 
(y’, ’$, ’) = (y’, A $, ’) 
(y’, $, ’i) = (zy, z $, ) 
(y, $, ), где = ’i, ’ = n, xy = x’y’, ’ = A .
109
Если (xy, S$, ) 
(y, $, ), то S
lm
x
Здесь первый переход включает n движений типа 1, а второй сам является
движением типа 1.
Завершающие pop-движения показывают,
что y’= zy, = z ; т. к. xy = x’y’ = x’zy, то x = x’z.
Последнее движение типа 1 было выполнено благодаря элементу M (A, u’) = ( , i)
для |
|
G |
|
что предполагает суще- |
1 |
( y ), |
|||
|
u FIRST |
|
|
|
ствование правила A под номером i.
110