Лекция 3 математическое моделирование

3.1 Основные понятия

Математические модели относятся к типу идеального моделирования, которое может быть интуитивным или знаковым.

Под интуитивным принято понимать моделирование, основанное на интуитивном представлении об объекте исследования, не поддающемся формализации либо не нуждающемся в ней. В этом смысле, например, жизненный опыт каждого человека может считаться его интуитивной моделью окружающего мира.

Знаковым называется моделирование, использующее в качестве моделей знаковые преобразования различного вида: схемы, графики, чертежи, формулы, наборы символов и т. д., включающие совокупность законов, по которым можно оперировать с выбранными знаковыми элементами. Знаковая модель рассматривается как лингвистическая, визуальная, графическая и математическая.

Модель лингвистическая – представлена некоторым лингвистическим объектом, формализованной языковой системой или структурой. Иногда такие модели называют вербальными, например, правила дорожного движения – языковая, структурная модель движения транспорта и пешеходов на дорогах.

Модель визуальная – позволяет визуализировать отношения и связи моделируемой системы, особенно в динамике. Например, на экране компьютера часто пользуются визуальной моделью объектов, клавиатуры в программе-тренажере по обучению работе на клавиатуре.

Модель графическая – представима геометрическими образами и объектами, например, макет дома является натурной геометрической моделью строящегося дома.

Важнейшим видом знакового моделирования является математическое моделирование, классическим примером которого является описание и исследование основных законов механики И. Ньютона средствами математики.

Классификация математических моделей.

По принадлежности к иерархическому уровню математические модели делятся на модели микроуровня, макроуровня, метауровня (см. рис. 3.1). Математические модели на микроуровне процесса отражают физические процессы, протекающие, например, при резании металлов. Они описывают процессы на уровне перехода (прохода). Математические модели на макроуровне процесса описывают технологические процессы. Математические модели на метауровне процесса описывают технологические системы (участки, цехи, предприятие в целом).

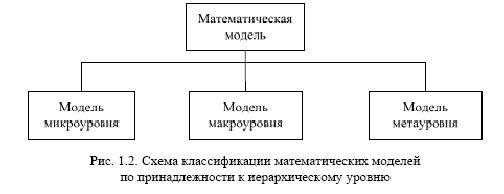
Рисунок 3.1 - Схема классификации математических моделей

по принадлежности к иерархическому уровню

По характеру отображаемых свойств объекта модели можно классифицировать на структурные и функциональные (рис. 3.2).

Рисунок 3.2 - Схема классификации математических моделей

по характеру отображаемых свойств объекта

Модель структурная – представима структурой данных или структурами данных и отношениями между ними; например, структурной моделью может служить описание (табличное, в виде графа, функциональное или другое) трофической структуры экосистемы. В свою очередь, структурная модель может быть иерархической или сетевой.

Модель иерархическая (древовидная) – представима некоторой иерархической структурой (деревом); например, для решения задачи нахождения маршрута в дереве поиска можно построить древовидную модель, приведенную на рис. 3.3.

Модель сетевая – представима некоторой сетевой структурой. Например, строительство нового дома включает операции, приведенные в нижеследующей таблице. Эти операции можно представить в виде сетевой модели, приведенной на рис. 3.4 и в табл. 3.1.

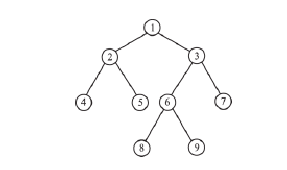
Рисунок 3.3. Модель иерархической структуры

Таблица 3.1 - Перечень работ при строительстве дома

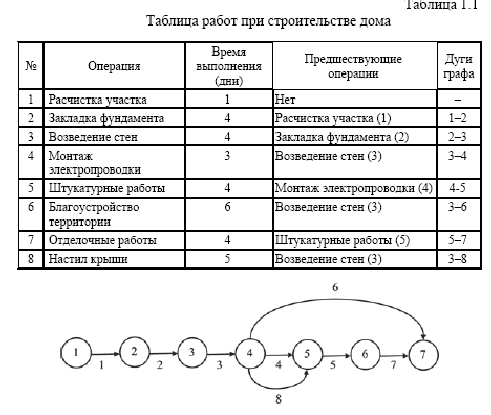
Рисунок 3.4. Сетевой график строительных работ

Модель функциональная – представима в виде системы функциональных соотношений. Например, закон Ньютона и модель производства товаров – функциональные.

По способу представления свойств объекта (рис. 3.5) модели делятся на аналитические, численные, алгоритмические и имитационные [18].

Рисунок 3.5. Схема классификации математических моделей

по способу представления свойств объекта

Аналитические математические модели представляют собой явные математические выражения выходных параметров как функций от параметров входных и внутренних и имеют единственные решения при любых начальных условиях. Например, процесс резания (точения) с точки зрения действующих сил представляет собой аналитическую модель. Также квадратное уравнение, имеющее одно или несколько решений, будет аналитической моделью.

Модель будет численной, если она имеет решения при конкретных начальных условиях (дифференциальные, интегральные уравнения).

Модель алгоритмическая – описана некоторым алгоритмом или комплексом алгоритмов, определяющим ее функционирование и развитие. Введение данного типа моделей (действительно, кажется, что любая модель может быть представлена алгоритмом её исследования) вполне обосновано, т. к. не все модели могут быть исследованы или реализованы алгоритмически. Например, моделью вычисления суммы бесконечного убывающего ряда чисел может служить алгоритм вычисления конечной суммы ряда до некоторой заданной степени точности. Алгоритмической моделью корня квадратного из числа Х может служить алгоритм вычисления его приближенного, сколь угодно точного значения по известной рекуррентной формуле.

Модель имитационная – предназначена для испытания или изучения возможных путей развития и поведения объекта путем варьирования некоторых или всех параметров модели, например модель экономической системы производства товаров двух видов. Такую модель можно использовать в качестве имитационной с целью определения и варьирования общей стоимости в зависимости от тех или иных значений объемов производимых товаров.

По способу получения модели делятся на теоретические и эмпирические.

Теоретические математические модели создаются в результате исследования объектов (процессов) на теоретическом уровне. Например, существуют выражения для сил резания, полученные на основе обобщения физических законов. Но они неприемлемы для практического использования, т. к. очень громоздки и не совсем адаптированы к реальным процессам обработки материалов.

Эмпирические математические модели создаются в результате проведения экспериментов (изучения внешних проявлений свойств объекта с помощью измерения его параметров на входе и выходе) и обработки их результатов методами математической статистики.

По форме представления свойств объекта модели делятся на логические, теоретико-множественные и графовые (рис. 3.6).

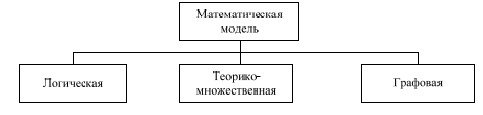
Рисунок 3.6 – Виды моделей по форме представления свойств объекта

Модель логическая – представима предикатами, логическими функциями, например, совокупность двух логических функций может служить математической моделью одноразрядного сумматора.

Модель теоретико-множественная – представима с помощью некоторых множеств и отношений принадлежности к ним и между ними.

Модель графовая – представима графом или графами и отношениями между ними.

Математическое моделирование – это замещение оригинала математической моделью, обеспечивающей фиксацию и исследование свойств и отношений оригинала, а также переход к оригиналу с помощью математических методов. Особое значение среди математических моделей имеют подобные, обеспечивающие перенос данных на оригинал на основании подобия.

Существенным моментом является то обстоятельство, что при изучении любого процесса методом математического моделирования необходимо в первую очередь построить его математическое описания (математическую модель). Математическая модель реальной системы является тем абстрактным формально описанным объектом, изучение которого возможно математическими методами (в том числе с помощью математического моделирования). Сложность и многообразие процессов функционирования реальных систем не позволяют строить для них абсолютно адекватные математические модели. Математическая модель, описывающая формализованный процесс функционирования системы, в состоянии охватить только основные (существенные для субъекта - релевантные) закономерности, оставляя в стороне второстепенные факторы.

Процесс математического моделирования реальных систем (процессов) опирается на критерий практики, что позволяет сделать вывод о правильности положений, лежащих в основе подлежащей изучению и использованию (гипотетической) модели. Поэтому процесс математического моделирования включает несколько этапов [мат энц.]:

- формулирование законов, связывающих основные объекты моделирования. Этот этап требует широкого знания фактов, относящихся к изучаемым явлениям, и глубокого проникновения в их зависимости. Эта стадия завершается записью в математических терминах сформулированных качественных представлений о связях между элементами модели;

- исследование математических задач, к которым приводит математическая модель. Основной вопрос исследования – решение прямой задачи – получение в результате анализа модели выходных данных (теоретических следствий) для дальнейшего их сопоставления с результатами наблюдений изучаемых явлений (систем, процессов);

- выяснение того, удовлетворяет ли принятая (гипотетическая) модель критерию практики, т.е. выяснение вопроса о том, согласуются ли результаты наблюдений (экспериментов) с теоретическими следствиями модели в пределах точности наблюдений. Если модель была вполне определена (все параметры были заданы), то определение уклонений теоретических следствий от наблюдений дает решение прямой задачи с последующей оценкой уклонений. Если уклонения выходят за пределы точности наблюдений, то модель не может быть принята. Часто при построении модели некоторые ее характеристики остаются неопределенными. Задачи, в которых определяются характеристики модели (параметрические, функциональные) таким образом, чтобы выходная информация была сопоставима в пределах точности наблюдений изучаемых явлений (систем, процессов) называются обратными задачами. Если математическая модель такова, что ни при каком выборе характеристик этим условиям нельзя удовлетворить, то модель непригодна для исследования рассматриваемых явлений (систем, процессов);

- последующий анализ модели в связи с накоплением данных об изучаемых явлениях и модернизация модели. В процессе развития науки и техники, данные об изучаемых явлениях уточняются, и наступает момент, когда выводы, получаемые на основании принятой модели, не соответствуют нашим знаниям о явлении (системе, процессе) – возникает необходимость построения новой, более совершенной математической модели.

Пример - модель Солнечной системы.

Наблюдения звездного неба начались в глубокой древности. Первичный анализ этих наблюдений позволил выделить планеты из всего многообразия небесных светил (выделение объектов изучения).

Второй шаг – определение закономерностей их движений:

- модель Птолемея (2 век н.э.) – планеты и Солнце совершают движение вокруг Земли (геоцентрическая модель). Движение описывалось с помощью правил (формул), многократно усложнявшихся по мере накопления наблюдений;

- модель Коперника (Н. Коперник, 1543 г.) – принципиально новая (гелиоцентрическая) модель – планеты вращаются вокруг Солнца. Причина появления – необходимость повышения точности наблюдений для нужд кораблевождения. Это качественная модель, в которой не существовало параметров системы (радиусы окружностей, угловые скорости движения и др.). Коперник вынужден был вводить поправки в характеристики движения планет по окружностям («эпициклы»);

- исследования И. Кеплера (начало 17 века), который сформулировал законы движения планет, что позволило кинематически описать движения, каждой планеты обособлено, не затрагивая причин, обуславливающих эти движения;

- работы И. Ньютона (2 половина 17 века) – динамическая модель Солнечной системы, основанная на законе всемирного тяготения. Динамическая система согласуется с кинематической моделью И. Кеплера (из нее следуют законы Кеплера);

- в 40-м году 19 века выводы динамической модели (по видимым планетам) пришли в противоречие с наблюдениями. Планета Уран уклонялась от теоретической траектории. У. Леверье (1846 г.) предсказал и вычислил новую планету (Нептун) и эта планета была открыта в предсказанном месте. Аналогично в 1930 году была открыта планета Плутон.