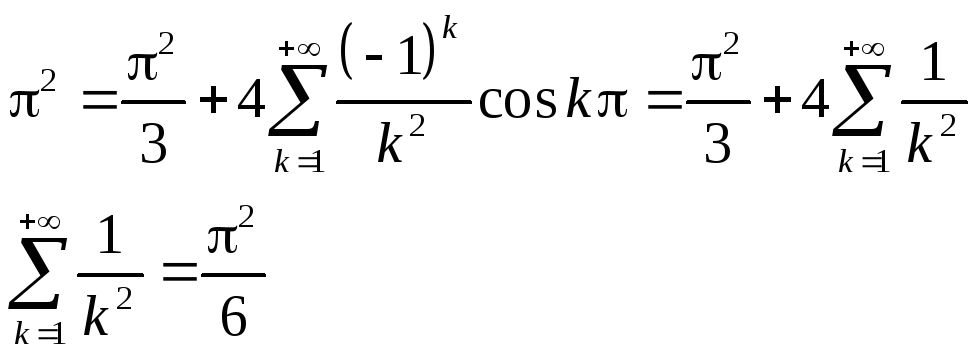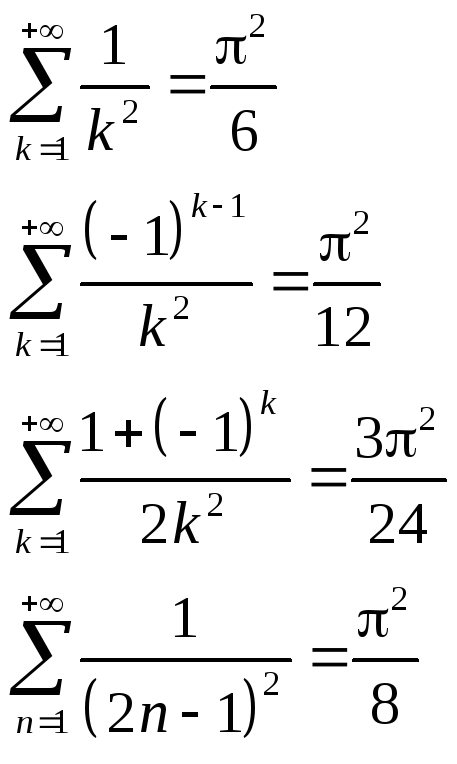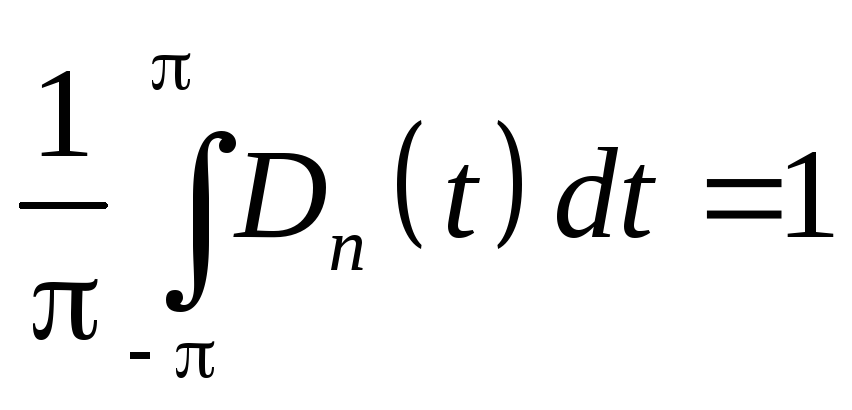Лекции / семестр4 / Лекции МП-2 (Альшина) / Pr7

§18. Тригонометрические ряды Фурье.

Рассмотрим f(x) - 2 - периодическую функцию: f(x+2)= f(x), кусочно непрерывную на [-,]. Поставим ей в соответствие ее тригонометрический ряд Фурье

,

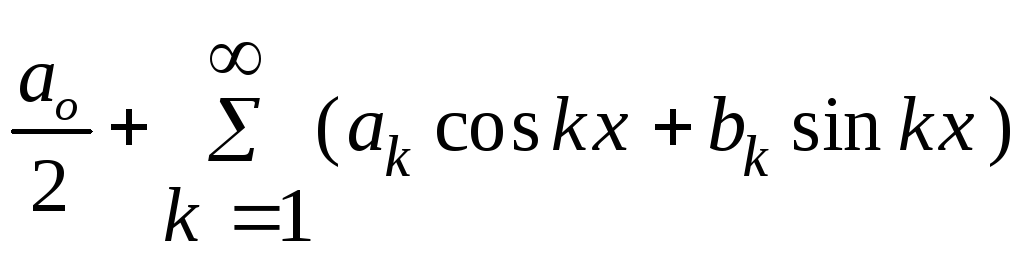где , ,

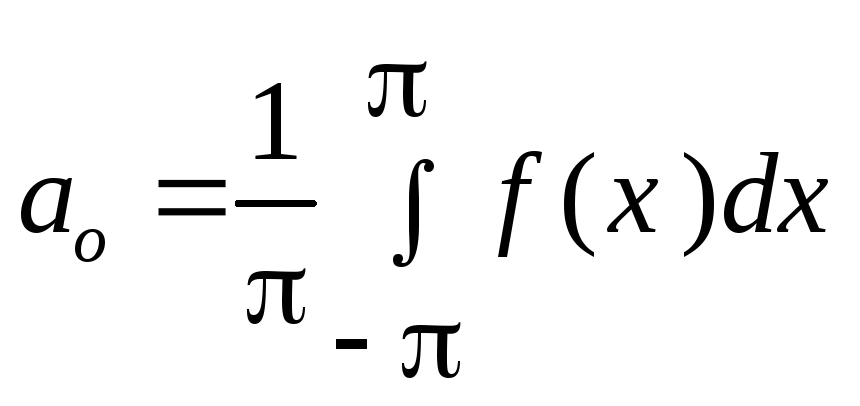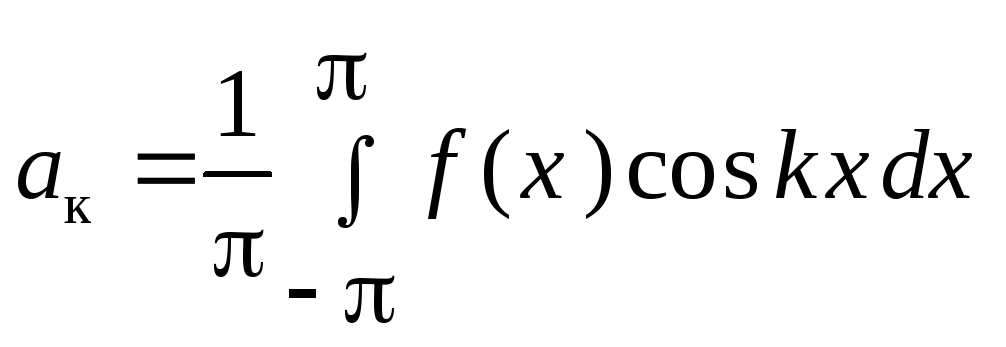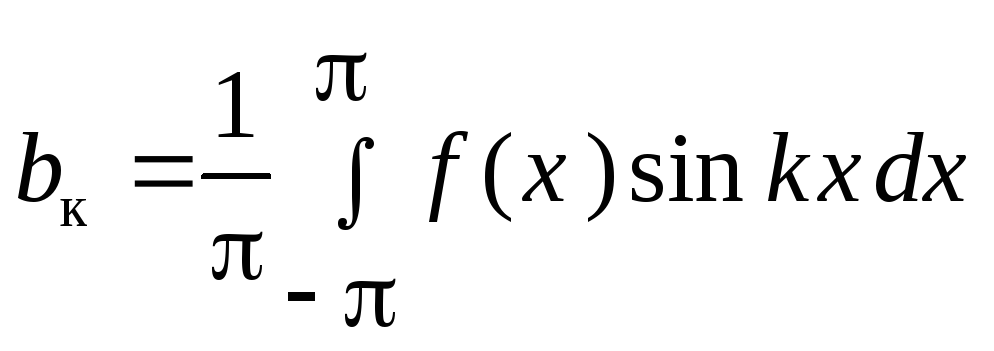
Частичная сумма тригонометрического ряда Фурье для функции f(x) с учетом формул для вычисления коэффициентов может быть преобразована следующим образом

,

где введена новая функция , называемая ядром Дирихле.

Свойства ядра Дирихле.

1. - непрерывная, четная, 2 - периодическая функция, причем

2. 

Доказательство

.

3. , при

Доказательство

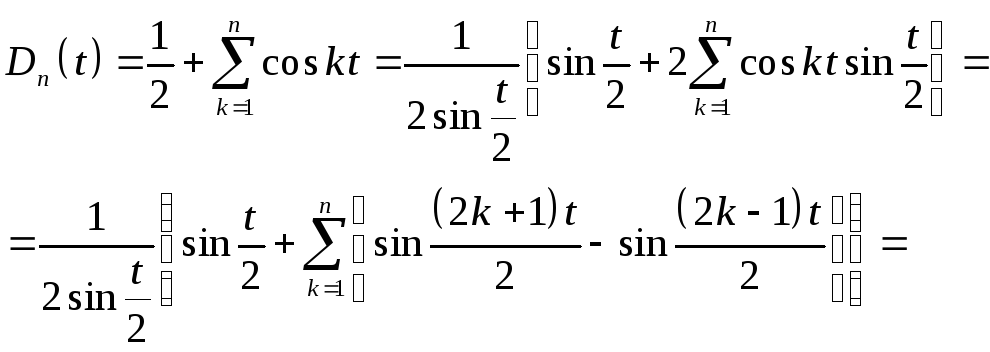
Т.о. частичная сумма ряда Фурье для функции f(x) представима в виде интеграла от функции f(x) и ядра Дирихле

Последний синхронный сдвиг пределов интегрирования возможен в силу 2 периодичности подынтегральной функции. Такое интегральное представление частичной суммы ряда Фурье носит название интеграла Дирихле.

Для доказательства поточечной сходимости тригонометрического ряда Фурье к 2 периодической функции нам потребуется следующая лемма.

Определение. Функция называется кусочно-гладкая, если она кусочно-непрерывна, имеет непрерывную производную за исключением, быть может, конечного числа точек, где производная имеет конечные односторонние пределы.

Лемма (Лебега) Если (x) –кусочно-гладкая функция на [a,b], тогда .

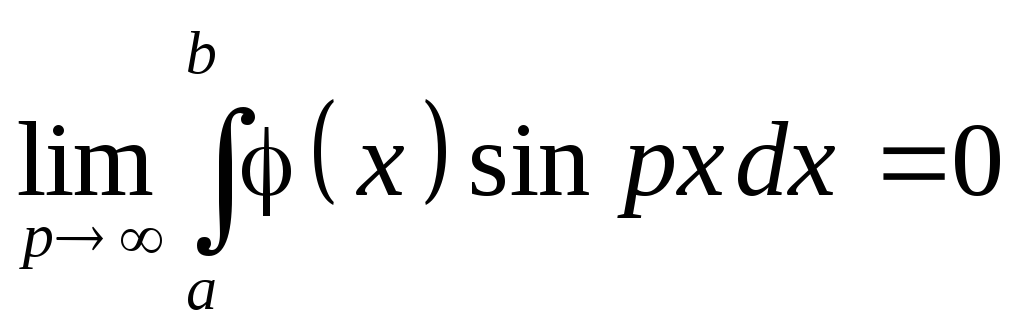Доказательство.

1. Отрезок [a,b] можно разбить на конечное число промежутков [x_k-1,x_k], на каждом из которых функция (x) будет непрерывно дифференцируема и  и .

Очевидно

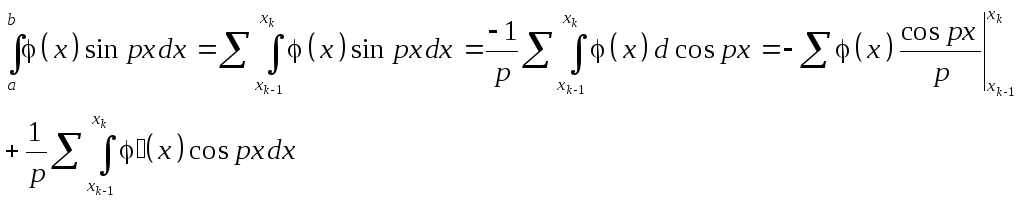
Замечание1. Требования Леммы Лебега можно ослабить и потребовать абсолютной интегрируемости

Замечание2. При тех же условиях, аналогично .

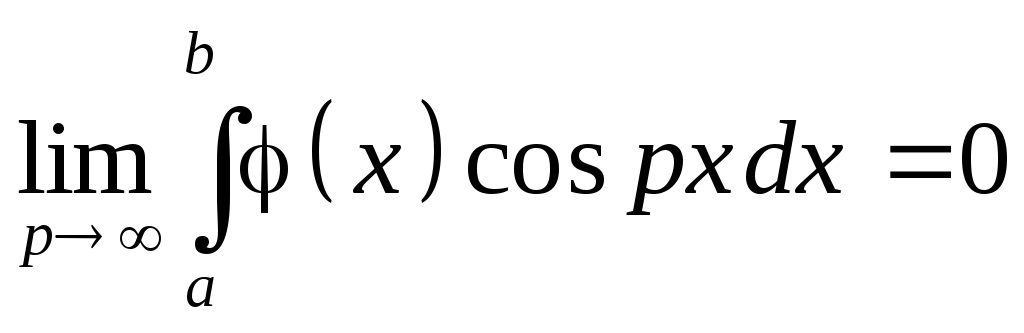Теорема. (О поточечной сходимости тригонометрического ряда Фурье) Пусть f(x) -2 периодическая функция, кусочно-гладкая, тогда ее тригонометрический ряд Фурье сходится всюду, причем его сумма равна .

Здесь f(x+0) (f(x-0)) соответственно правое (левое) предельное значение функции.

Доказательство.

Рассмотрим разность полусуммы предельных значений функции и частичной суммы ее ряда Фурье

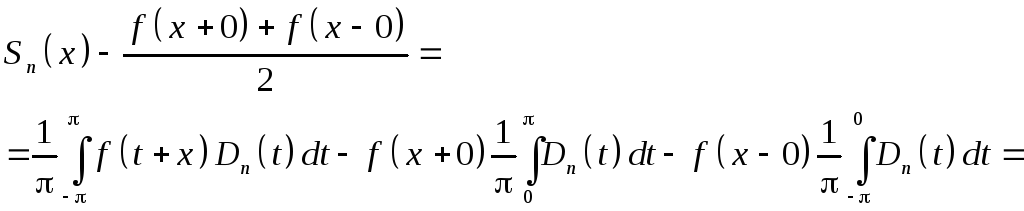
Здесь мы воспользовались свойствами ядра Дирихле

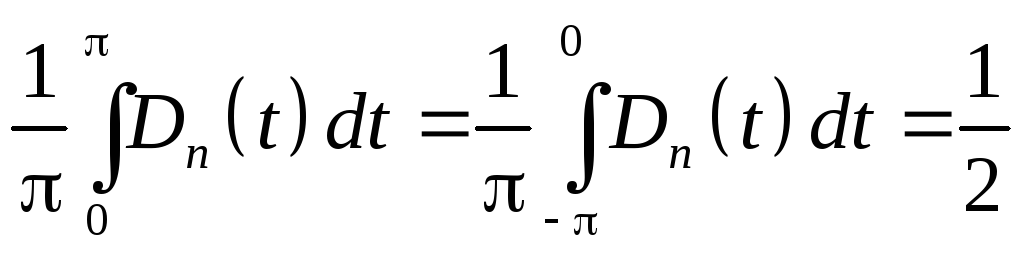
Докажем, что это выражение при достаточно больших n может быть сделано < для . Для этого представим его в виде суммы четырех интегралов.

(*)

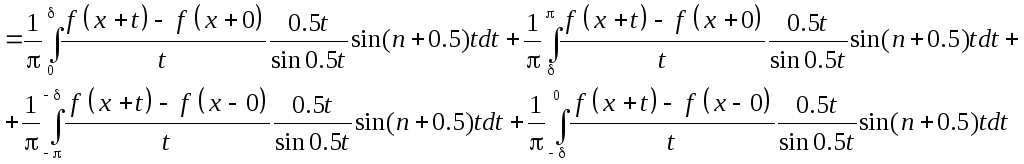Рассмотрим первый из них

.

Оценим модуль подынтегрального выражения. Первый множитель

и

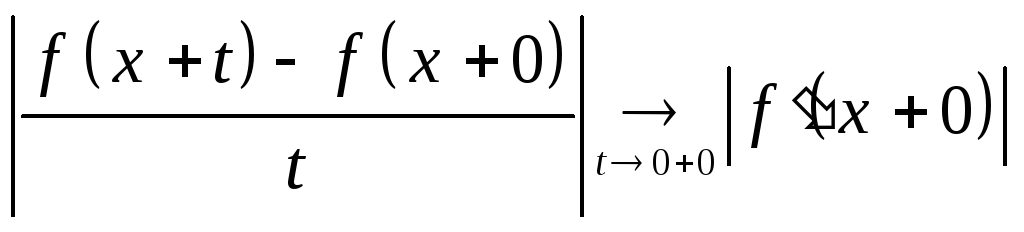
значит при достаточно малом 

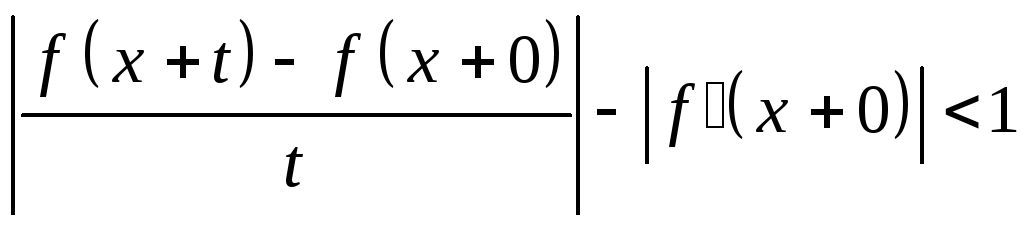или

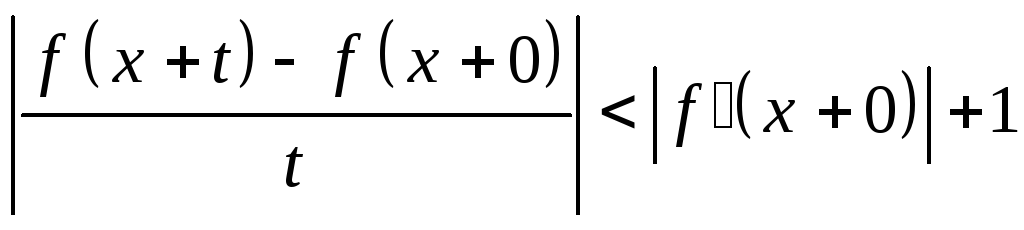
Второй множитель

значит при достаточно малом 

или

Третий множитель вообще всегда

Тогда

Совершенно аналогично может быть оценен и четвертый интеграл в (*).

Второй и третий интегралы представляют собой интегралы вида , где кусочно-гладкие функции. В силу Леммы Лебега эти интегралы стремятся к 0, значит  n:

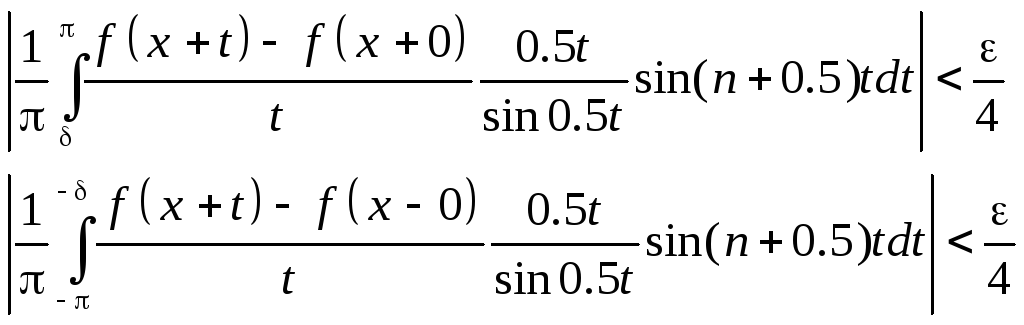
Т.о. из (*) следует, что

.

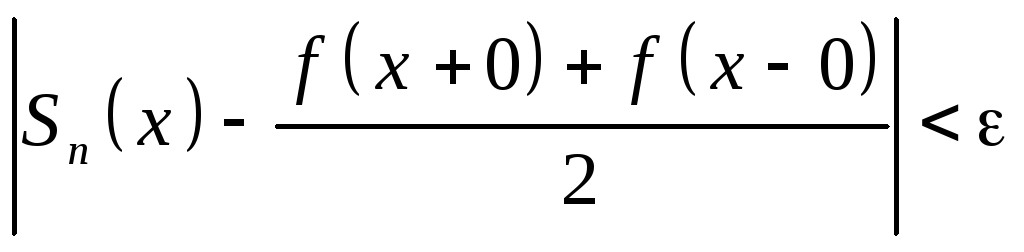Замечание 1. Мы показали, что тригонометрический ряд Фурье для кусочно непрерывной  периодической функции сходится к ней в точках непрерывности и к полусумме предельных значений в точках разрывов первого рода.

Замечание 2. Ряд Фурье может быть построен и для непериодической функции, заданной на . Для кусочно-гладкой функции ряд Фурье будет сходиться к ней (или полусумме предельных значений в точках разрыва) внутри . Очевидно, за пределами этого интервала ряд Фурье сходится к -периодическому продолжении исходной функции.

Замечание 3. Требования теоремы можно ослабить. Например, справедлив Признак Дини

Пусть f(x) -2 периодическая функция, интегрируемая функция и при  x и  >0 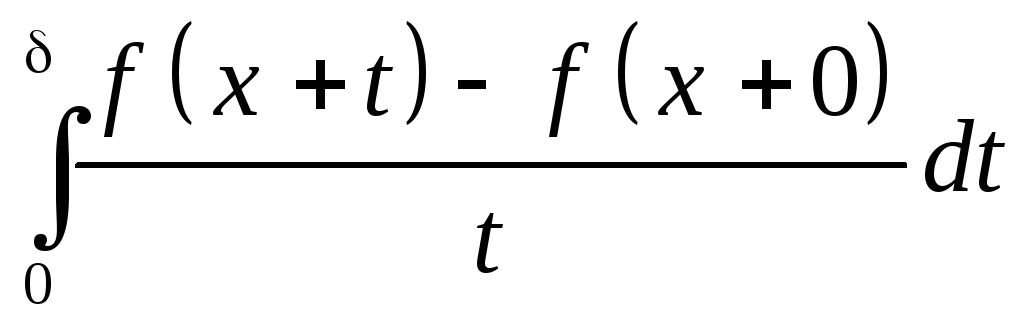 и .

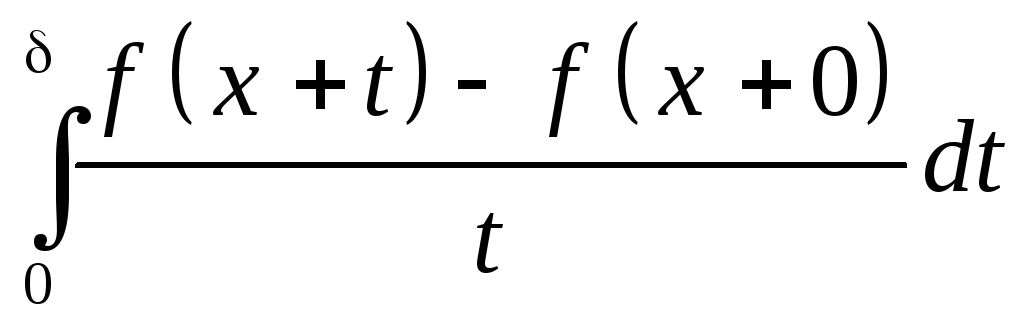Тогда ее тригонометрический ряд Фурье сходится всюду, причем его сумма равна .

Примеры.

1.

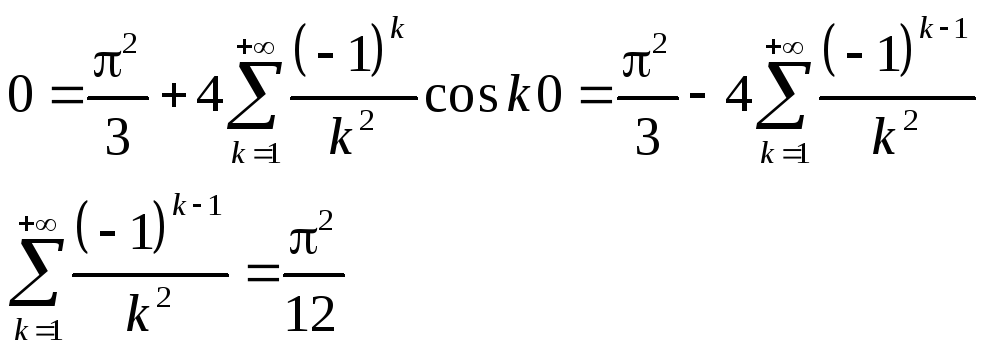
5