
Лекции / семестр4 / Лекции МП-2 (Альшина) / Pr6
.doc§16. Ортонормированные системы функций,
-
Евклидовы пространства
Проблема разложения функции в ряд Фурье является обобщением и развитием идеи разложения вектора по базису.
Из курса линейной алгебры известно, что
если в линейном пространстве конечной
размерности выбрать некоторый базис,
то
![]() элемент
пространства может быть разложен по
этому базису. Сложность лишь в том, что
пространство функций бесконечномерно,
т.е. можно найти любое сколь угодно
большое число линейно независимых
функций. Особенно удобным (из курса
линейной алгебры) является ортогональный
базис. В этой главе мы построим
ортогональный базис в пространстве
функций.
элемент
пространства может быть разложен по
этому базису. Сложность лишь в том, что
пространство функций бесконечномерно,
т.е. можно найти любое сколь угодно
большое число линейно независимых
функций. Особенно удобным (из курса
линейной алгебры) является ортогональный
базис. В этой главе мы построим
ортогональный базис в пространстве
функций.
О
Линейное пространство (в частности,
пространство функций) называется
евклидовым, если в нем задано
правило, посредством которого
![]() f и g
– элементам этого пространства ставится
в соответствие действительное число,
называемое скалярным произведением
и указанное правило удовлетворяет
следующим аксиомам:
f и g
– элементам этого пространства ставится
в соответствие действительное число,
называемое скалярным произведением
и указанное правило удовлетворяет
следующим аксиомам:
1o (f,g) = (g,f) (переместительное свойство)
2o (f+g,h) = (f,h) + (g,h) ( распределительное свойство)
3o
(f,g)
= (f,g)
для
![]()
![]() Real
Real
4o (f,f) > 0, если f – ненулевой элемент
(f,f) = 0, если f - нулевой элемент
Пример. Рассмотрим пространство функций кусочно-непрерывных на сегменте [a,b], т.е. непрерывных всюду, за исключением быть может конечного числа точек, где функция имеет разрыв 1-го рода. В точках разрыва xi доопределим функцию
![]()
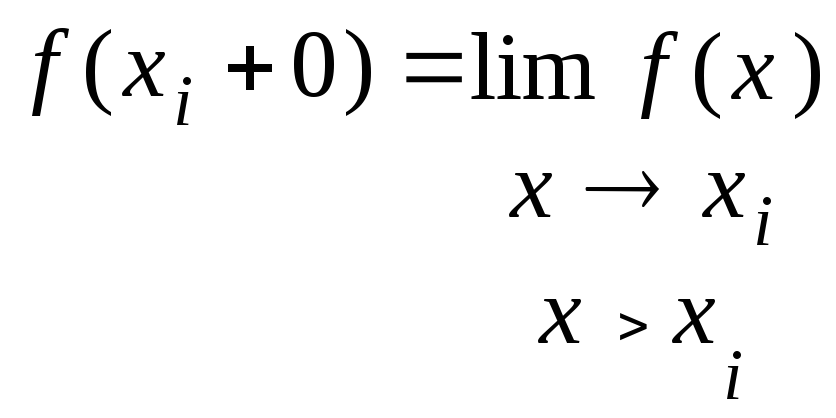

Введем скалярное произведение по
правилу
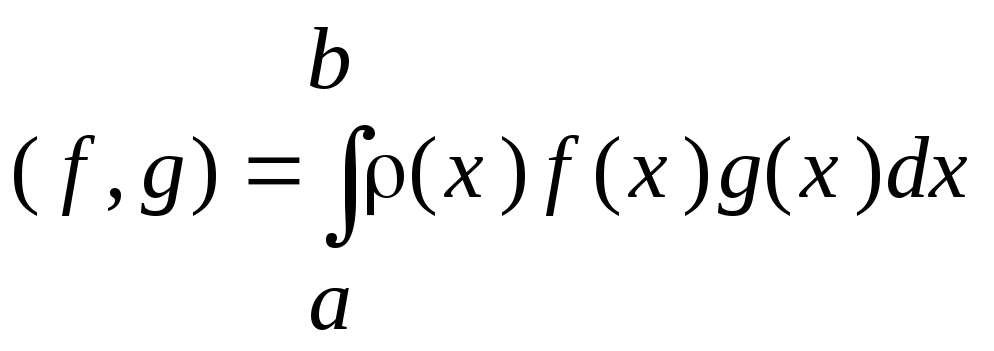 ,
где
,
где
![]() -
произвольная весовая функция
-
произвольная весовая функция
![]() .
.
Проверим выполнение аксиом скалярного произведения.
1o,2o и 3o выполнены в силу линейных свойств интеграла.
4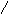 o
o
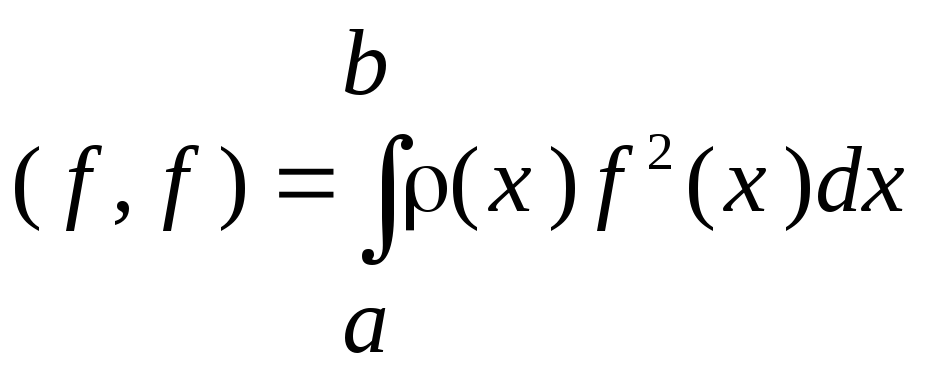
![]() Под интегралом стоит неотрицательная,
отличная от 0 функция
Под интегралом стоит неотрицательная,
отличная от 0 функция
![]() интеграл
положителен
интеграл
положителен
![]()
![]() Под
интегралом 0
Под
интегралом 0
![]() значение интеграла 0 (f,f)=0
значение интеграла 0 (f,f)=0
Т.о. введённое нами функциональное
пространство является евклидовым.
Оно имеет название
![]()
Для элементов евклидова пространства справедливы следующие свойства:
1)
![]() -
неравенство Коши-Буняковского
-
неравенство Коши-Буняковского
Доказательство:
![]() (f-g,
f-g)
(f-g,
f-g)![]() 0
( По аксиоме 4о)
0
( По аксиоме 4о)
2(f,f)-2(f,g)
+(g,g)![]() 0
- это квадратный трехчлен относительно
.
0
- это квадратный трехчлен относительно
.
Необходимое и достаточное условие неотрицательности квадратного трехчлена является неположительность его дискриминанта
т.о. (f,g)2-(f,f)(g,g)![]() 0
0
(f,g)2![]() (f,f)(g,g).
(f,f)(g,g).![]()
2) Во всяком евклидовом пространстве
можно ввести понятие нормы элемента
(![]() ),
),
определенное как
![]()
Норма элемента евклидова пространства обладает следующими свойствами:
1о
![]() ,
если f - не нулевой элемент
,
если f - не нулевой элемент
![]() ,
если f - нулевой элемент
(следует из аксиомы 4о)
,
если f - нулевой элемент
(следует из аксиомы 4о)
2о![]()
![]()
![]() Real.
Real.
3о
![]() (неравенство треугольника)
(неравенство треугольника)
Д
![]() (неравенство
К-Б)
(неравенство
К-Б)
![]()
В частности для евклидова пространства
![]() неравенства
Коши-Буняковского и треугольника
принимают вид:
неравенства
Коши-Буняковского и треугольника
принимают вид:
неравенство Коши-Буняковского.
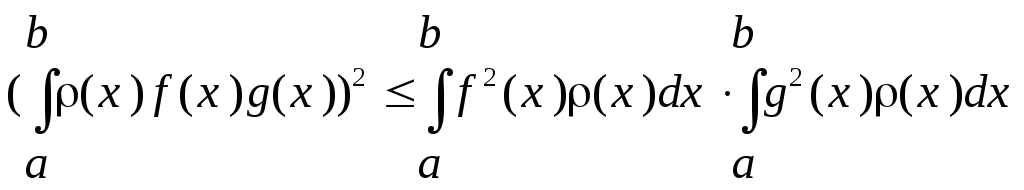
неравенство треугольника.
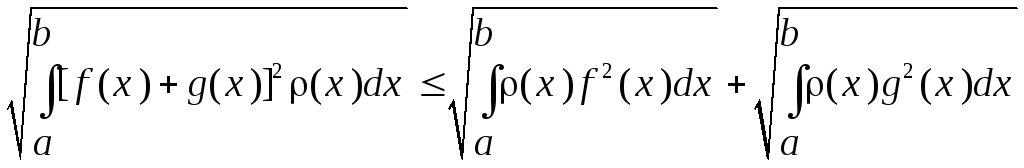
2. Ортогональность элементов евклидова пространства
О Два элемента евклидова пространства называются ортогональными, если их произведение равно 0.
![]()
Рассмотрим в бесконечномерном евклидовом пространстве бесконечную последовательность элементов 1, 2 , 3, ... {к}
О Последовательность {к}называется ортонормированной системой , если
(к,
m)
=
![]() =
=
![]()
В этом случае все элементы системы попарно ортогональны и норма каждого элемента равна 1.
Классическим примером ортонормированной
системы в пространстве
![]() (весовая
функция
(весовая
функция
![]() ,
в этом случае в названии пространства
ее опускают) является тригонометрическая
система.
,
в этом случае в названии пространства
ее опускают) является тригонометрическая
система.
![]()
Легко проверить ортонормированность тригонометрической системы.
Д
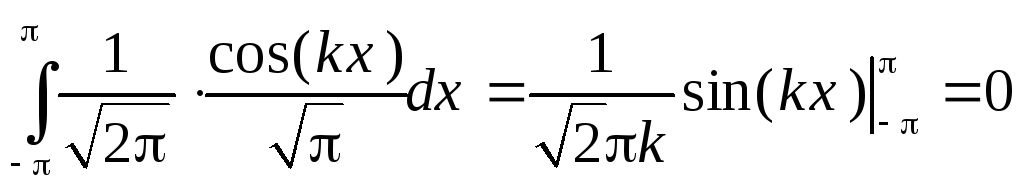
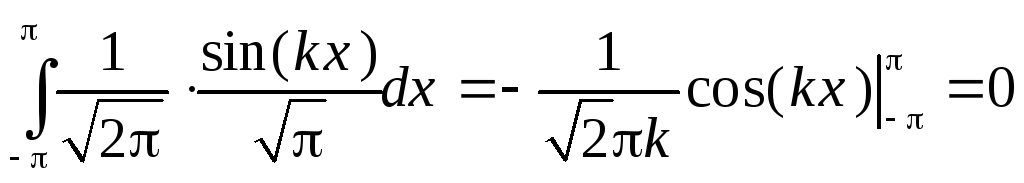
![]()

Аналогично
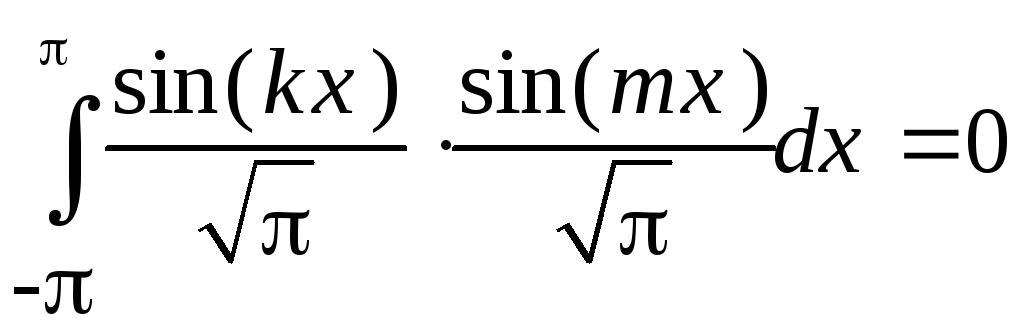
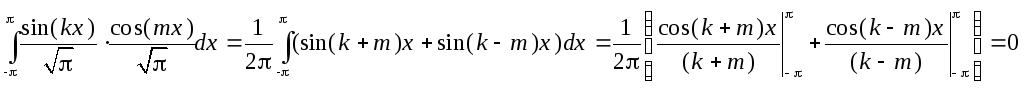 и
так далее.
и
так далее.
Т.о. все функции тригонометрической систему попарно ортогональны.
Квадраты норм всех функций :
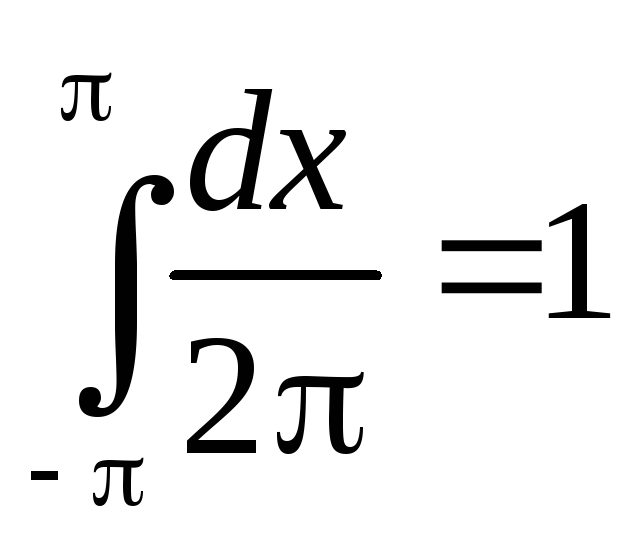
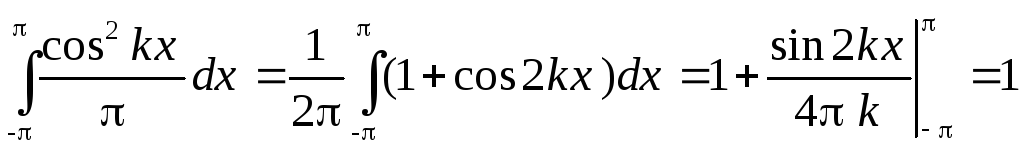
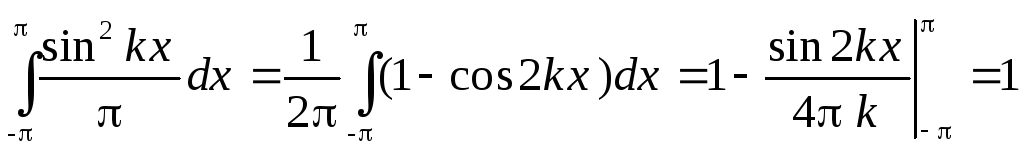
Известны и другие ортонормированные системы функций
1)Полиномы Лежандра ортогональны на
[-1,+1] с весом
![]()
![]() n=0,1,2
…
n=0,1,2
…
2) Полиномы Чебышева
![]()
![]()
ортогональны на [-1,1] с весом
![]()
3) Полиномы Эрмита
![]() ортогональны
на
ортогональны
на
![]() с
весом
с
весом
![]()
и другие.
![]() ,
,
![]() ,
,
![]() ,
,
![]() …
…
§17 Общий ряд Фурье
-
Задача о наилучшем среднеквадратичном приближении
Пусть в произвольном бесконечномерном евклидовом пространстве задана ортонормированная система элементов {к}
О Назовём рядом Фурье элемента f по ортонормированной системе {к}
ряд вида
![]() fk
к,
где fk=(f,
к)
– коэффициенты Фурье элемента f
fk
к,
где fk=(f,
к)
– коэффициенты Фурье элемента f
O
Конечная сумма Sn=![]() fk
к
-
частичная сумма ряда Фурье.
fk
к
-
частичная сумма ряда Фурье.
Рассмотрим произвольную линейную комбинацию из n первых элементов ортонормированной системы {к}
![]() Ckк
Ckк
с произвольными постоянными Ck
Выясним, что отличает частичную сумму
ряда Фурье
![]() fk
к
от
любой другой суммы
fk
к
от
любой другой суммы
![]() Ck
к
Ck
к
О
![]() -
отклонение элемента f
от элемента g в норме
данного евклидова пространства.
-
отклонение элемента f
от элемента g в норме
данного евклидова пространства.
Т17.1
Среди всех сумм вида
![]() Ck
к
наименьшее отклонение от элемента f
имеет n-ная частичная его
ряда Фурье
Ck
к
наименьшее отклонение от элемента f
имеет n-ная частичная его
ряда Фурье
![]() fk
к
fk
к
Д
![]() ||
||
![]() Ck
к-f
||2 = (
Ck
к-f
||2 = (![]() C
k
к
- f,
C
k
к
- f,
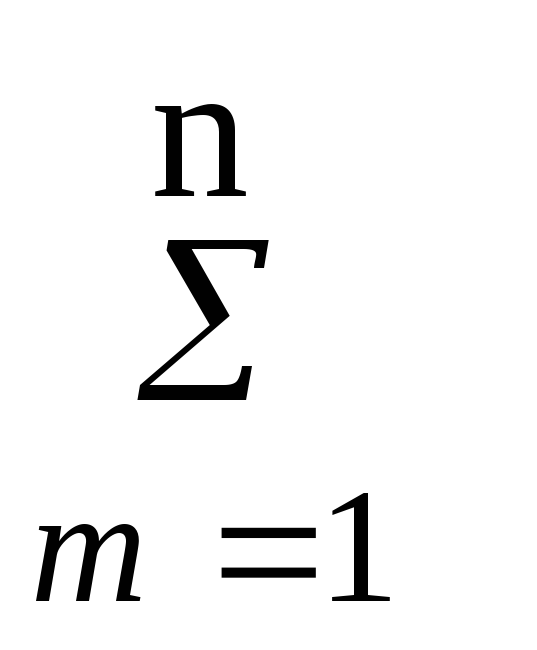 Cm
m
- f) =
Cm
m
- f) =
= (![]() Ck
к,
Ck
к,
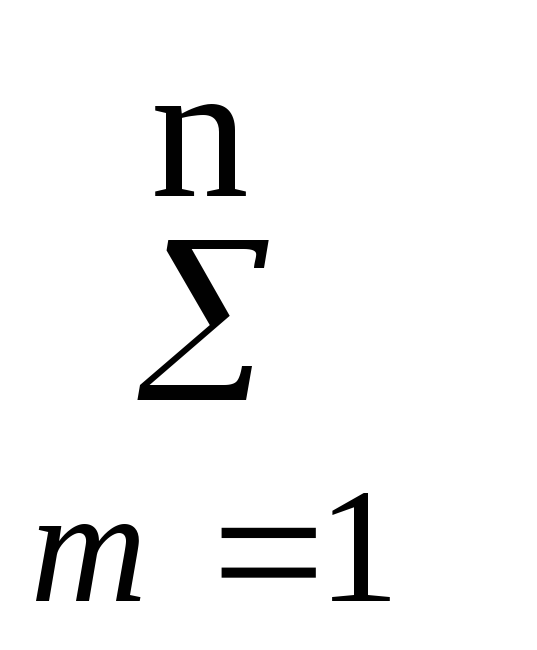 Cm
m)
- 2
Cm
m)
- 2![]() Ck(к,f)
+ (f,f)
=
Ck(к,f)
+ (f,f)
=
Учитывая, что (к,
m)=
![]()
![]() Ck2
- 2
Ck2
- 2![]() Ckfk
+
Ckfk
+![]() =
=![]() Ck2
- 2
Ck2
- 2![]() Ckfk
+
Ckfk
+![]() fk2
-
fk2
-![]() fk2
+
fk2
+![]() =
=
=![]() (Ck-
fk)
2
-
(Ck-
fk)
2
-![]() fk2+
fk2+![]()
![]()
Минимум отклонения
![]() Ckк
от f достигается
при Ck=
fk,
т.к. первое слагаемое обращается в 0, а
остальные от Ck
не зависят.
Ckк
от f достигается
при Ck=
fk,
т.к. первое слагаемое обращается в 0, а
остальные от Ck
не зависят.
Следствие 1.
![]() f,
f,
![]() n,
n,
![]() {к}-
ортонормированной системы и
{к}-
ортонормированной системы и
![]() набора Ck
набора Ck
![]() -
-
![]() fk2
fk2
![]() ||
||![]() Ck
к-f
||2
Ck
к-f
||2
Следствие 2. ||![]() fk
к
- f||2
fk
к
- f||2![]()
![]() -
-
![]() fk2
– тождество Бесселя
fk2
– тождество Бесселя
Замечание. По Т17.1 частичная сумма ряда Фурье реализует наилучшее среднеквадратичное приближение к элементу f евклидова пространства среди всевозможных линейных комбинаций первых n элементов ортонормированной системы {к}.
-
Неравенство Бесселя
Т17.2
Для
![]() f
– элемента данного бесконечномерного
евклидова пространства и
f
– элемента данного бесконечномерного
евклидова пространства и
![]() {к}-
ортонормированной системы справедливо:
{к}-
ортонормированной системы справедливо:
![]() -
неравенство Бесселя
-
неравенство Бесселя
Д
![]() Вспомним тождество Бесселя ||
Вспомним тождество Бесселя ||![]() fk
к
- f ||2
fk
к
- f ||2![]()
![]() -
-
![]() fk2
fk2
левая часть в нем неотрицательна
![]()
![]() n
n
![]() fk2
fk2![]()
![]()
Т.о. Частичные суммы ряда
![]() fk2
из неотрицательных членов ограничены
сверху. Такой ряд сходится. Неравенство
выполняется для
fk2
из неотрицательных членов ограничены
сверху. Такой ряд сходится. Неравенство
выполняется для
![]() n
n
![]() при n
при n![]() оно так же верно
оно так же верно
![]()
![]() .
.![]()
Понятие полноты ортогональной системы.
Определение. Ортогональная система
функций {к}
называется полной в евклидовом
пространстве
![]() ,
если для произвольного элемента f
этого пространства его ряд Фурье по
ортогональной системе
,
если для произвольного элемента f
этого пространства его ряд Фурье по
ортогональной системе
![]() fk
к
fk
к
сходится в среднем к этому элементу, т.е.
![]() .
.
В этом случае {к} образует базис в пространстве.
Вспомнив тождество Бесселя
||![]() fk
к
- f ||2
fk
к
- f ||2![]()
![]() -
-
![]() fk2
fk2
и устремим
![]() .
Для полной системы {к}
правая часть этого тождества обращается
в 0. Т.о. для полных систем справедливо
.
Для полной системы {к}
правая часть этого тождества обращается
в 0. Т.о. для полных систем справедливо
![]() -
равенство Парсеваля.
-
равенство Парсеваля.
Определение. Ортогональная система
функций {к}
называется замкнутой в евклидовом
пространстве
![]() ,
если единственный элемент этого
пространства, ортогональный всем
функциям {к},
это нулевой элемент.
,
если единственный элемент этого
пространства, ортогональный всем
функциям {к},
это нулевой элемент.
Теорема. Всякая полная система является замкнутой.
Доказательство.
Пусть элемент fn n. Рассмотрим его ряд Фурье.
Все коэффициенты Фурье элемента f
будут равны
![]() в силу ортогональности этого элемента
всем {к}. Тогда
в силу равенства Парсеваля
в силу ортогональности этого элемента
всем {к}. Тогда
в силу равенства Парсеваля
![]() .
Но единственный элемент, имеющий норму
равную 0, - это по свойствам нормы нулевой
элемент.
.
Но единственный элемент, имеющий норму
равную 0, - это по свойствам нормы нулевой
элемент.
Тригонометрический ряд Фурье.
О Тригонометрический ряд Фурье – ряд Фурье по тригонометрической системе
![]()
ортонормированной на
![]() .
.
Для
![]() кусочно-непрерывной
на
кусочно-непрерывной
на
![]() функции f(x)
тригонометрический ряд Фурье имеет вид
функции f(x)
тригонометрический ряд Фурье имеет вид
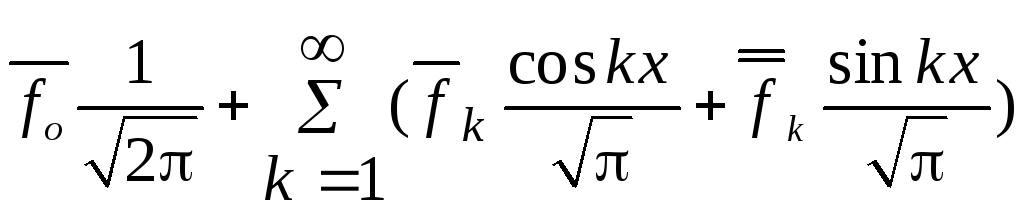 ,
где
,
где
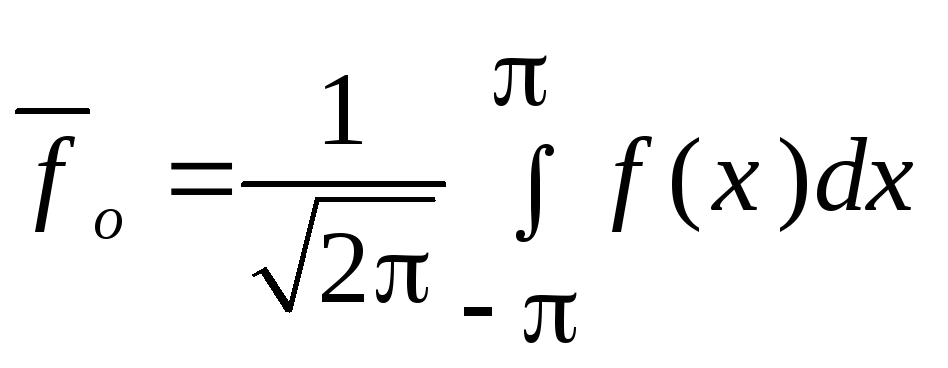
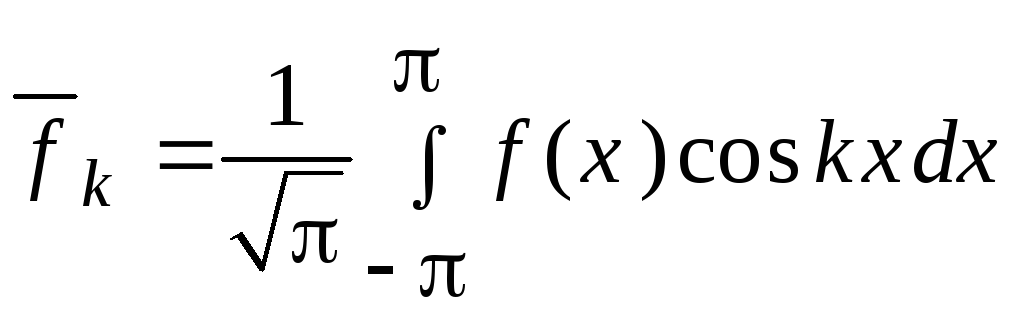
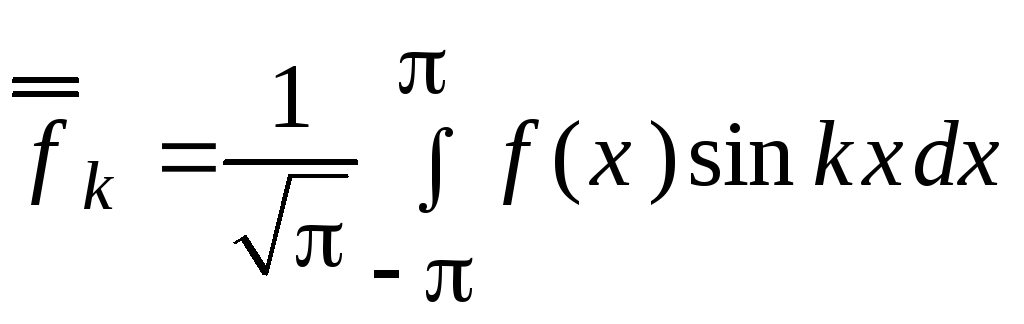
Неравенство Бесселя в этом случае имеет
вид:

В теории тригонометрических рядов Фурье обычно применяется несколько другая форма записи коэффициентов тригонометрического ряда Фурье
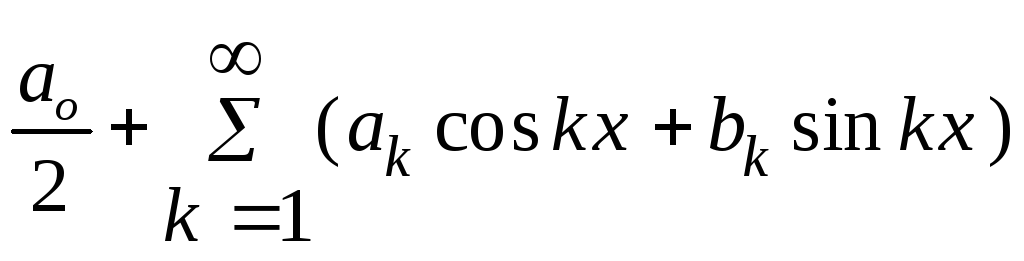 ,
где
,
где
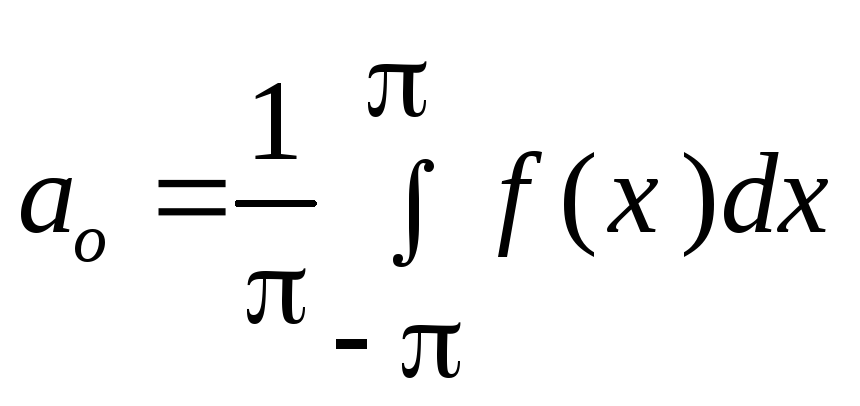

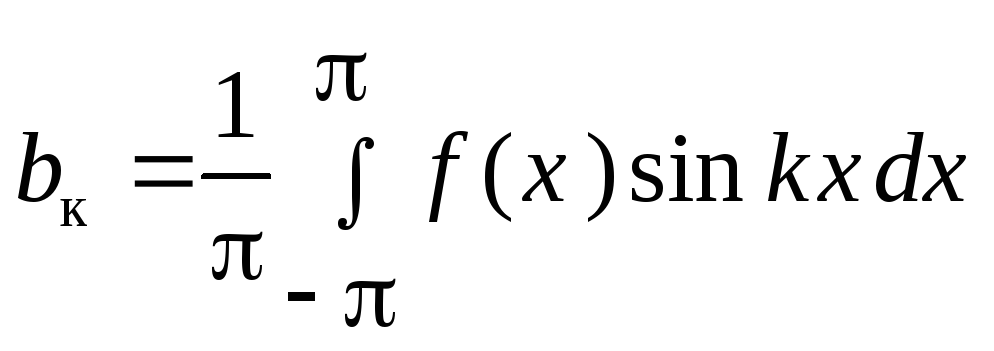
Для этой формы записи неравенство
Бесселя
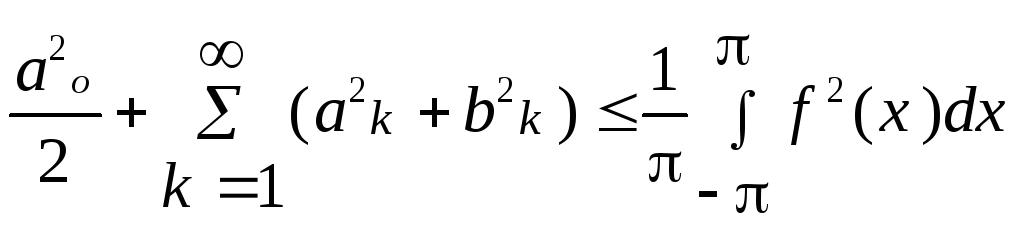 .
.
Замечание. Из неравенства Бесселя
вытекает, что для
![]() кусочно-непрерывной
на
кусочно-непрерывной
на
![]() f(x),
ее тригонометрические коэффициенты
Фурье стремятся к 0 с ростом их номеров.
f(x),
ее тригонометрические коэффициенты
Фурье стремятся к 0 с ростом их номеров.
![]() (
в силу необходимого условия сходимости
ряда в неравенстве Бесселя).
(
в силу необходимого условия сходимости
ряда в неравенстве Бесселя).
