Лекции / семестр4 / Лекции МП-2 (Альшина) / Pr13

§37. Однородное уравнение теплопроводности с неоднородными начальными условиями.

,,

,

Здесь мы взяли для определенности граничные условия Неймана на обеих границах и конкретизировали начальные условия, по ходу изложения станет понятно, что метод универсален и не зависит от этого выбора.

Разделение переменных приводит к равенству, обе части которого зависят лишь от одной переменной, это возможно лишь тогда, когда обе они равны константе

Для пространственной части, получаем снова задачу Штурма-Лиувилля, которая в данном конкретном случае имеет вид

.

Общее решение этой задачи имеет вид

.

Из граничных условий находим допустимые значения 

 B=0

 , n=1,2,3,…

Т.о. найдены собственные значения

и собственные функции задачи Ш-Л

.

Подставим найденное _n в уравнение для временной части

Его решение

.

Общий вид решения задачи для однородного уравнения теплопроводности

.

Неизвестные коэффициенты T_n найдем из начальных условий.

Решение исходной задачи может быть представлено своим рядом Фурье по ортогональной системе СФ задачи Ш-Л

.

Т.о. коэффициенты T_n находятся из Фурье разложения начального условия по СФ задачи Ш-Л. Для нахождения такого разложения помножим обе части равенства на СФ и проинтегрируем

.

В силу ортогональности СФ задачи Ш-Л в правой части останется только коэффициент T_m помноженный на квадрат нормы СФ

.

Заметим, пока вид СФ не конкретизировался, т.е. метод подойдет для любого вида СФ и общий вид решения задачи для однородного уравнения теплопроводности с неоднородными начальными условиями

, где ,

Применительно к рассматриваемой задаче с конкретными начальными и граничными условиями

.

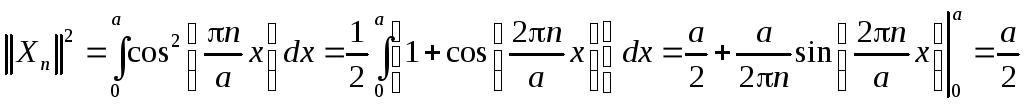
Т.о. решение исходной задачи

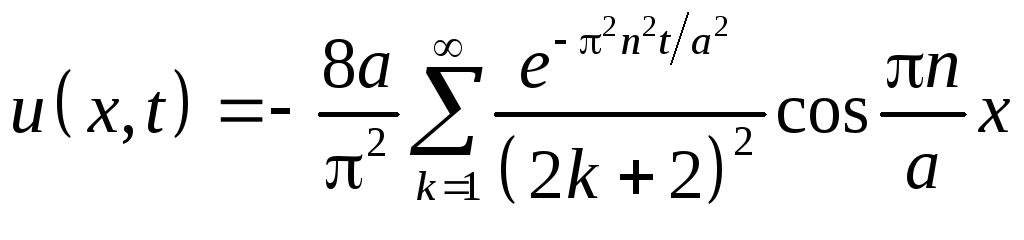
Заметим, что с течением времени гармоники с высокими номерами затухают быстрее, чем гармоники с низкими номерами. Такая картина характерна для решений задач теплопроводности.

§38. Неоднородное уравнение теплопроводности с однородными начальными условиями.

,,

.

Будем искать решение этой задачи при помощи разложения в ряд Фурье по СФ задачи Ш-Л. Рассмотрим для начала однородное уравнений, проведем в нем разделение переменных, для пространственной части получим опять задачу Ш-Л, которая в случае данных краевых условий имеет вид

.

Ее СФ и СЗ .

Т.о. . Подставим в исходное уравнение, разложив функцию в правой части так же в ряд Фурье по системе СФ задачи Ш-Л :

Из задачи Ш-Л найдем , тогда

,

приравнивая слагаемые при одинаковых базисных функциях, получим ОДУ для временной части решения

.

Общее решение такого ОДУ второго порядка имеет вид

.

Учитывая нулевые начальные условия

находим недостающие коэффициенты A_n

.

Т.о. для временной части

Т.о. решение начально-краевой задачи для неоднородного уравнения теплопроводности с однородным начальным условием

, где

Для конкретного типа краевых условий и правой части уравнения, получим

.
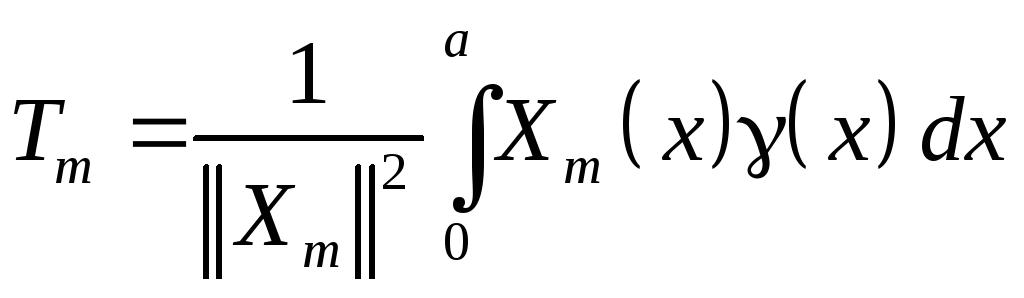