Лекции / семестр4 / Лекции МП-2 (Альшина) / Pr8

§19. Равномерная сходимость тригонометрического ряда Фурье.

Ряд Фурье составлен из непрерывных функций. По теореме 14.1 ряд из непрерывных функций, сходящийся равномерно, сходится к непрерывной функции. Мы доказали, что ряд Фурье может сходится не только к непрерывной функции, но и к функции, имеющей разрывы первого рода. Отсюда следует, что сходимость ряда Фурье далеко не всегда равномерная. Очевидно, для равномерной сходимости ряда Фурье нужно потребовать как минимум непрерывности функции, но оказывается и этого не достаточно. Существуют примеры непрерывных функций, ряд Фурье для которых расходится.

Достаточный признак равномерной сходимости ряд Фурье можно сформулировать, например, так.

Теорема (о равномерной сходимости ряда Фурье) Пусть f(x) - 2 периодическая, непрерывная, кусочно-гладкая, тогда ее тригонометрический ряд Фурье сходится к ней равномерно.

Доказательство.

Чтобы доказать равномерную сходимость ряда Фурье

воспользуемся мажорантным признаком Вейерштрасса. Для этого нужно доказать сходимость мажорирующего числового ряда

, или, что равносильно сходимость ряда .

По условию теоремы - кусочно непрерывная функция. Обозначим ее коэффициенты Фурье

, .

Тогда для коэффициентов Фурье исходной функции получим, интегрируя по частям

,

,

Т.к. в силу периодичности функции

.

Итак

.

По условию - кусочно непрерывна, а значит интегрируема на .

Значит для ее ряда Фурье выполнено неравенство Бесселя

Из чего следует, что ряд сходится.

Далее, из очевидных неравенств

вытекают неравенства

и .

Следовательно

Больший ряд сходится, следовательно по признаку сравнения сходится и меньший.

Из сходимости мажорантного ряда по признаку Вейерштрасса следует равномерная сходимость ряда Фурье

.

Замечание. Мы использовали в доказательстве ряд Фурье для производной, сходимость которого, вообще говоря, не гарантируется.

Свойство равномерной сходимости очень важно для почленного дифференцирования и интегрирования функциональных рядов.

Скорость сходимости ряд Фурье.

Перейдем к изучению вопроса о скорости сходимости тригонометрического ряда Фурье.

Теорема 19.3. Пусть f(x) - 2 периодическая, непрерывная, имеет непрерывную производную , удовлетворяющую на всей числовой оси неравенству , тогда коэффициенты Фурье удовлетворяют неравенствам, .

Т.е. коэффициенты Фурье убывают как .

Учитывая 2 периодичность исходной функции, интегрируем по частям s раз

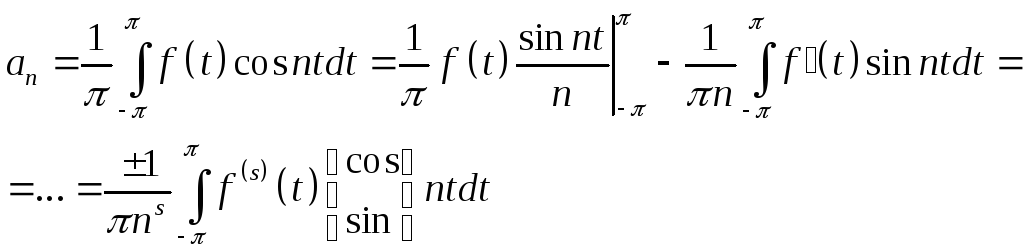
Т.о.

_{Аналогично получаем и вторую оценку.}

Пример 1. Разложить в ряд Фурье функцию , .

Эта функция непрерывна, т.к. ее знаменатель не обращается в 0.

Используем замену и , где , получим

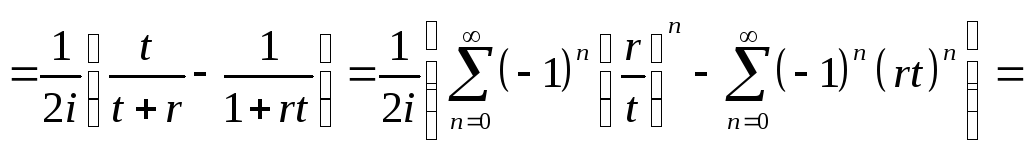
Пример 2. Разложить в ряд Фурье функцию , .

У этой непрерывной функции существует ряд Фурье. Производная ее также непрерывна на всей числовой оси

Воспользовавшись результатом предыдущего разложения, получим

Интегрируя почленно, получим

Положив x=0, определим константу C

Сравнивая с известным разложением в ряд Тейлора

Получим С=0.

Т.о.

§20. Ряды Фурье функций с произвольным периодом.

Для функций, периодических с периодом 2l справедливо следующее разложение в ряд Фурье

,

где

.

Для получения этих формул достаточно сделать замену переменной , при помощи которой отрезок отображается на отрезок .

§21. Комплексная форма рядов Фурье.

Используя замену Эйлера и , получим

,

где

, , n=1,2,3,…

, где n=0,1, 2, 3,…

Т.о. справедлива комплексная форма записи ряда Фурье