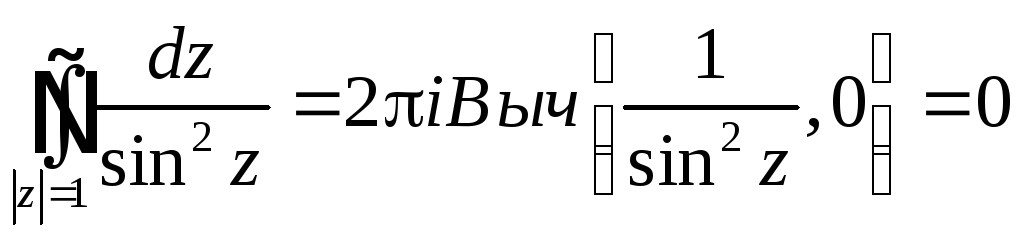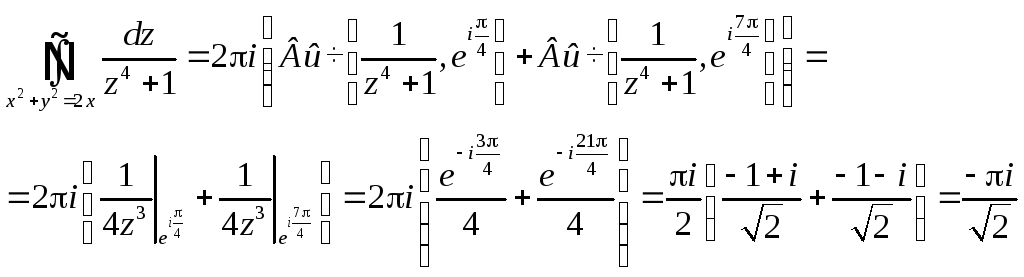Лекции / семестр4 / Лекции МП-2 (Альшина) / Pr2

§25.Понятие вычета аналитической функции в изолированной особой точке.

Пусть z₀ - изолированная особая точка аналитической f(z). Тогда f(z)=c_n(z-z₀)ⁿ; 0<|z-z₀|< , где . Легко видеть, что особую роль играет коэффициент c_-1.

Определение . Комплексное число Выч[f(z),z₀]= , где С - замкнутый контур, который можно стянуть к z₀ , оставаясь в кольце аналитичности функции f(z)- называется вычетом f(z) в точке z₀.

Замечание. Иногда вычет обозначают еще Res[f(z),z₀].

Очевидно Выч [f(z),z₀]=c_-1.

В ряде случаев можно указать более простой способ вычисления вычета, сводящийся к дифференцированию f(z) в окрестности z₀. Т.о. вычисление ряда интегралов становится особенно простым при использовании теории вычетов.

1. Формулы вычисления вычетов.

1. z₀- устранимая особая точка. Выч [f(z),z₀]= c_-1=0.

2. z₀ - полюс 1-го порядка.

f(z)=c_-1(z-z₀)^-1+c0+c₁(z-z₀)¹ +…

Если f(z)=(z)/(z), (z₀)0, (z)=(z-z₀)'(z₀)+...; '(z₀)0, то

Выч [f(z),z₀]= =(z₀)/ '(z₀).

3. z₀ - полюс порядка m>0.

f(z)= c_-m(z-z₀)^-m…+c_-1(z-z₀)^-1+c₀+c₁(z-z₀)¹ +…

f(z) (z-z₀)^m= c_-m+c_-m+1(z-z₀)…+c_-1(z-z₀)^m-1+с₀(z-z₀)^m+…

Взяв производную порядка m-1 от обеих частей равенства



.

4. z₀- существенно особая: Выч [f(z),z₀]= c_-1.

Примеры.

1. 

z=0 – полюс m-го порядка

Выч [f(z),0]=

z=-1 – полюс 1-го порядка

Выч [f(z),-1]=

2. 

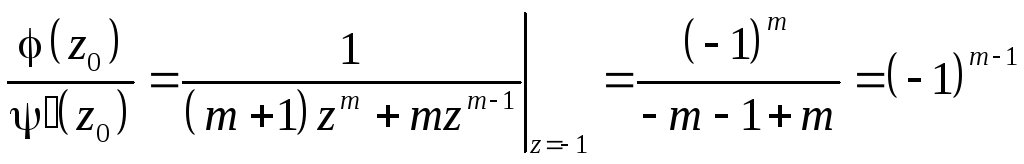
z=0 – существенно особая точка Выч [f(z),0]= c_{_1}=-1

3. - полюса первого порядка .

Выч [f(z),z_k]=

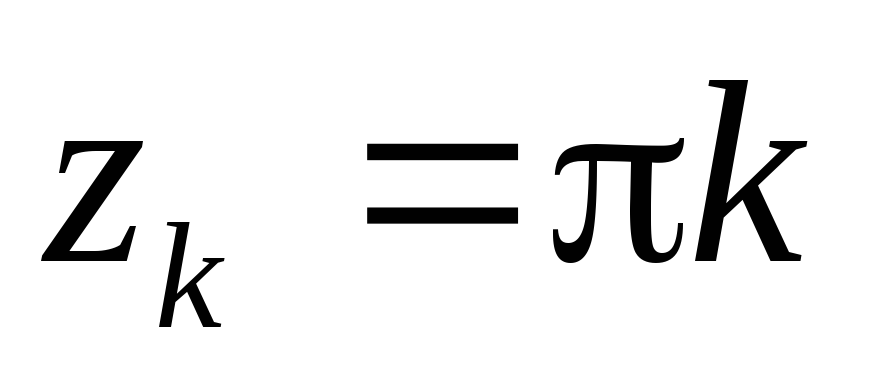4. - полюса 1-го порядка.

Выч [f(z),z_k]=1/cosz_k=

5. 

z=0 и z= – существенно особые точки

Выч [f(z),0]= Выч [f(z),]=0, т.к. разложение f(z) в ряд Лорана содержит только четные степени z, т.о. c_-1=0.

6. 

=0 (z=0) – точка ветвления

=k (z=²k²) – полюса первого порядка (k0)

Выч [f(z), z_k]=

7)

2. Основная теорема теории вычетов.

Основная теорема теории вычетов. Пусть f(z)C^(\z₁,z₂,...,z_N) за исключением конечного числа N изолированных особых точек, лежащих внутри g z_ng для n. Тогда .

Доказательство. Выделим каждую из изолированных особых точек z_n функции f(z) замкнутым контуром _n, не содержащих внутри других особых точек, кроме z_n. В замкнутой многосвязной области, ограниченной и всеми контурами _n, f(z) является всюду аналитической. По теореме Коши для многосвязной области

.

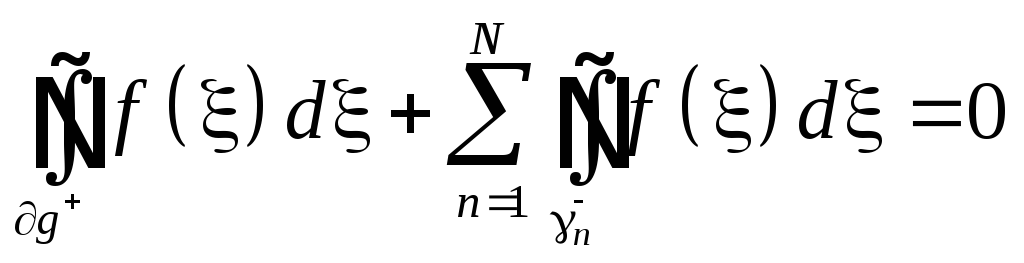Перенеся второе слагаемое направо, поменяв направление обхода контуров, использовав определение вычета получим искомое . 

3. Вычет в бесконечно удаленной точке.

Пусть z₀= - изолированная особая точка аналитической f(z).

Определение. Вычетом f(z) в z₀= называется комплексное число

Выч [f(z),]==-c_-1,

где C – произвольный замкнутый контур, вне которого f(z) не имеет особых точек кроме z=.

Замечание. Если z= - устранимая особая точка, то вычет в ней может быть отличен от 0.

Вторая теорема о вычетах. Пусть f(z)C^(\z₁,z₂,...,z_N=) на всей комплексной плоскости за исключением N-1 конечных изолированных особых точек и z_N= - изолированной особой точки. Тогда .

Доказательство. Рассмотрим C – произвольный замкнутый контур, содержащий внутри себя все N-1 конечных изолированных особых точек z₁,z₂,...,z_N-1. По основной теореме о вычетах

.

Но интеграл слева по определению равен - Выч [f(z),z_N=], т.о. .

Обе теоремы о вычетах помогают вычислить интеграл по замкнутому контуру от функции f(z) аналитической везде за исключением конечного числа изолированных особых точек, включая z=.

.

Здесь изолированные особые точки пронумерованы так, что z_n при n от1 до M лежат внутри контура C, а при n от M+1 до N - вне контура C.

Т.о. интеграл по замкнутому контуру от функции f(z) равен 2i на сумму вычетов во всех изолированных особых точках внутри контура.

Примеры.

1)

2. 

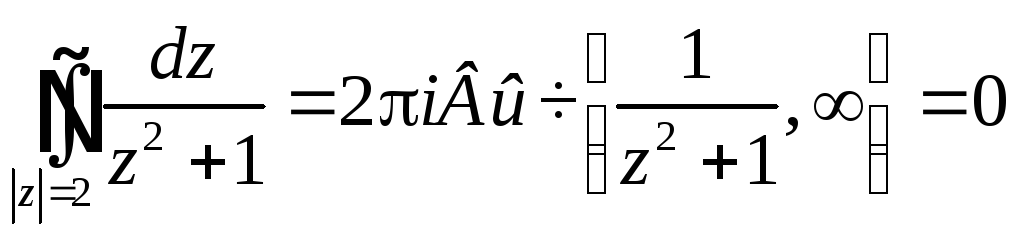
Здесь учтено, что - четная функция  ее разложение в ряд Лорана не содержит нечетных степеней z  c_-1=0.

2. 

3. 

4.