2.6 Проверка требований к спроектированной системе

2.6.1 Относительная интервальность

Проверим выполнение условия (2):

Условие не выполняется.

2.6.2 Дисперсия выхода системы

Согласно заданию, в случае, если условие (2) не выполняется, необходимо оценить влияние угловых реализаций интервальных параметров 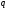на значение относительной дисперсии выхода системы.

Параметры 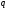представимы в аддитивной форме в виде:

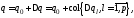
где 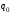– медианное значение параметров,­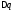– вариация,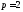в силу того что в системе (7) имеется только два интервальных параметра. Вычислить значения параметров можно по формуле:

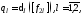(8)

где ­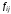– элементы матрицы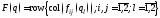системы (7). Для спроектированной системы получаем следующие значения параметров:

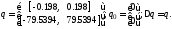
Дисперсия выхода системы 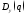вычисляется согласно формуле:

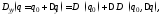(9)

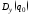
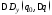
где ­ – дисперсия выхода системы при медианном значении параметров,­ – приращение дисперсии выхода системы, порождаемое вариацией вектора параметров.

Для того чтобы воспользоваться уравнением Ляпунова для нахождения дисперсии 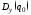, образуем агрегированную систему из системы (7) и формирующего фильтра (4).

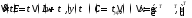(10)

где матрицы имеют вид

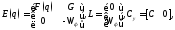
и примем 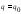. Тогда искомая дисперсия находится из выражения

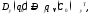(11)

где ­­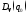– решение уравнения Ляпунова вида:

(12)

где . Интенсивность белого шумаNвыразим из формулы дисперсии формирующего фильтра:

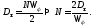
Подставляя числовые значения, получаем .

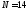Воспользовавшись функцией lyapпакетаMatlabдля решения (12), получаем следующий результат:

Тогда дисперсия выхода системы при медианном значении параметров системы (7) равна

Приращение дисперсии выхода для системы (7) имеет представление:

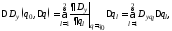(13)

Теперь поставим задачу вычисления функции чувствительности 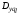дисперсии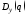для спроектированной системы (7). Как показано ранее, дисперсия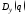может быть найдена из уравнения вида (12). Продифференцируем выражение (12) по компоненту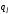вектора параметров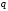в точке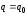

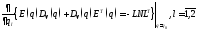
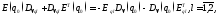(14)

где

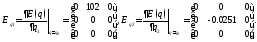
Воспользовавшись функцией lyapпакетаMatlab, получаем следующие результаты:

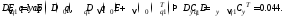
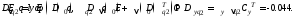
Тогда приращение дисперсии выхода, являющее собой оценку влияния вариации угловых реализаций интервальных параметров на значение дисперсии, будет равно:

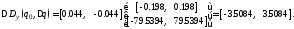
Подставляем полученные составляющие дисперсии выхода системы в (9):

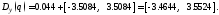
Рассчитаем теперь относительное значение дисперсии:

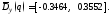
3 Моделирование

3.1 Переход к дискретному описанию системы

Формирование стохастической составляющей задающего воздействия связано с математической проблемой нереализуемости непрерывного белого шума , но реализуемостью дискретного белого шума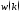. В этой связи от непрерывного описания системы необходимо перейти к дискретному.

3.1.1 Шаг дискретизации

Величина шага дискретизации задаётся исходя из требования адекватности отображения непрерывного сигнала его дискретной выборкой:

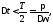
где – период,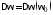– полоса пропускания модели. Выберем полосу пропускания, соответствующую построенной ПДММ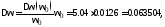а шаг дискретизации соответственно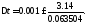

3.1.2 Дискретная модель формирующего фильтра

Используем оператор Matlab’а c2d для дискретизации модели ФФ (4):

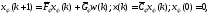
где матричные компоненты удовлетворяют условиям

,

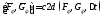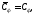
и получают представление:

3.1.3 Генератор дискретного белого шума

Для простоты оценивания сигналов, сигнал белого шума будем задавать с нормальным распределением. Тогда значение дисперсий оцениваемых сигналов, находящихся в интервале значений , можно будет вычислить по формуле

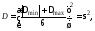(15)

где – среднеквадратичное отклонение.

При моделировании в программной оболочке Matlab, для получения дискретного белого шума с нормальным распределением можно воспользоваться блоком random number, где необходимо задать дисперсию дискретного белого шума – параметр "variance", V. Настраиваем значение «variance» ГДБШ таким образом, чтобы на выходе ФФ (9) наблюдался сигнал с дисперсией