Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

Санкт-Петербургский государственный университет

низкотемпературных и пищевых технологий

Кафедра информатики и прикладной математики

ИНФОРМАТИКА

И

ЗАЩИТА ИНФОРМАЦИИ

Санкт-Петербург

2011

УДК 681.3.06

А.М. Радин. Информатика и защита информации: Конспект лекций для студентов магистрантов и аспирантов всех специальностей. – СПб.: СПбГУНиПТ, 2008, 42 с.

Конспект лекций содержат в сжатом виде материал, необходимый для изучения курсов “Информатика”, “Защита информации”, а также курса “Компьютерные технологии в науке и производстве” студентами, магистрантами и аспирантами Санкт-Петербургского государственного университета низкотемпературных и пищевых технологий.

Рецензент

Проф. Л.А.Акулов

Рекомендовано к изданию редакционно-издательским советом университета.

© Санкт-Петербургский государственный

университет низкотемпературных

и пищевых технологий, 2011

Лекция 1.

Введение.

Разработкой методов преобразования (шифрования, зашифрования) информации с целью защиты её от незаконных пользователей занимается криптография. Дешифрование (расшифрование) - процесс, обратный шифрованию, с помощью определённых правил, содержащихся в шифре.

Криптография – прикладная наука, она использует самые

последние достижения фундаментальных наук, и в первую

очередь, математики.

Какие решаются при этом задачи?

Это в основном задачи, решаемые удалёнными абонентами в формате различных протоколов.

Примеры:

1. Протокол подписания контракта.

Нельзя допустить ситуацию, когда один абонент получил подпись другого, а сам не подписался.

2. Протокол подбрасывания монеты (принятие решения).

Нужно сделать так, чтобы абонент, подбрасывающий монету, не мог изменить результат после получения догадки от абонента, угадывающего этот результат.

3. Протокол идентификации абонента. Взаимодействуют два абонента (А - клиент, В - банк). Абонент А хочет доказать В, что он именно А, а не противник.

4. Взаимодействуют абоненты, получающие приказ из одного центра. Часть абонентов, включая центр, могут быть противниками. Необходимо выработать единую стратегию действий, выигрышную для абонентов. Эту задачу называют задачей о византийских генералах, а протокол её решения – протоколом византийского соглашения.

Основу решения указанных и других задач составляет интерактивная система доказательств. Это математическая наука, базирующаяся на новейших достижениях математики.

P, V, S протоколы.

Под интерактивной системой доказательства (P,V,S) (Prove , Verify, Statement) понимают протокол взаимодействия двух абонентов: P (доказывающий) и V (проверяющий). Абонент P хочет доказать V, что утверждение S истинно. При этом абонент V самостоятельно, без помощи P , не может проверить утверждение S (поэтому V и называется проверяющим). Абонент P может быть и противником, который хочет доказать V, что утверждение S истинно, хотя в действительности оно ложно. Протокол может состоять из многих раундов обмена и должен удовлетворять двум условиям:

1. Полнота – если S действительно истинно, то абонент P убедит абонента V признать это.

2. Корректность – если S ложно, то абонент P вряд ли убедит абонента V, что S истинно.

Подчеркнём, что в определении системы (P,V,S) не допускалось, что V может быть противником. А если V оказался противником, который хочет выведать у P какую-нибудь новую полезную для себя информацию об утверждении S? В этом случае P, естественно, может не хотеть, чтобы это случилось в результате работы протокола (P,V,S). Протокол (P,V,S), решающий такую задачу, называется протоколом с нулевым разглашением и должен удовлетворять, кроме условий 1) и 2), ещё и следующему условию:

3. Нулевое разглашение – в результате работы протокола (P,V,S) абонент V не увеличит свои знания об утверждении S или, другими словами, не сможет извлечь никакой информации о том, почему S истинно.

Уровни защищаемой информации.

1

2

3

4

Рис.1 Уровни защищаемой информации компьютера

Информацию защищают как локально (на отдельных компьютерах ) так и глобально (в сети Internet). Уровни защищаемой информации компьютера схематически изображены на рис.1.

Уровень 1 – это аппаратное обеспечение компьютера – система BIOS (Basic Input Output System). Система BIOS обеспечивает возможность защиты компьютера паролем включения CMOS (Complementary Metal-Oxide Semiconductor). Пароль включения снимается путём отключения аккумулятора, поддерживающего автономное электропитание CMOS.

Уровень 2 – это операционная система компьютера (например, Windows XP, Unix, Linux). Операционные системы защищают паролями доступа, имеющимися в каждой из них, и которые контролируются, как правило, системными администраторами.

Уровень 3 – это приложения – комплекс программ, при помощи которых создаётся деловая документация (Office, графические редакторы и другие программы). Приложения также защищают паролями доступа, имеющимися в каждом из них.

Уровень 4 – деловая документация (файлы и папки), доступ к которым также может быть защищён паролями. Однако самый надёжный способ защиты деловой документации – это её шифрование.

В процессе обмена между деловыми структурами конфиденциальная информация циркулирует в открытой сети (например, Internet) в зашифрованном виде, потому что создание и обслуживание для этой цели секретных каналов связи экономически не оправдано.

Технические аспекты защиты информации.

Из технических аспектов, касающихся защиты информации, следует отметить возможность дистанционного перехвата информации путём регистрации электромагнитного излучения от компьютеров комплексами специальной высокочувствительной измерительной аппаратуры типа TEMPEST (Transient Electromagnetic Pulse Emanations Standard). Это аппаратура двойного назначения. Она предназначена также и для защиты компьютеров от внешнего электромагнитного зондирования. Производитель комплексов TEMPEST - США , потребитель, в основном, Китай.

Разрабатывается также аппаратура для дистанционного считывания информации через сети электропитания компьютеров.

Для эффективной защиты конфиденциальной информации от дистанционного перехвата необходимо экранировать помещения, в которых находятся компьютеры, а также иметь их автономное электропитание. И ещё, при изготовлении, например, плат памяти компьютеров всегда существуют некоторые неконтролируемые аппаратно количества бит в платах (например, в пределах погрешности измерительной аппаратуры). Учитывая современные высоко компактные технологии изготовления плат, этого неконтролируемого количества бит вполне достаточно для размещения на платах в процессе их изготовления коротких программ, например, несанкционированного считывания паролей и пересылки их заказчику по сети.

Схема обмена конфиденциальной информацией в открытой сети.

Взаимодействуют два абонента A и B. Абонент A кодирует документ, затем, как правило, архивирует его (сжимает), затем шифрует и передаёт абоненту B по каналу связи. Абонент B действует в обратном порядке: дешифрует, деархивирует, декодирует документ. В этой схеме защита конфиденциальности информации обеспечивается только надёжностью шифрования, поскольку исключить возможность перехвата информации в открытой сети практически невозможно.

Кодирование информации.

Компьютеры кодируют информацию стандартным кодом ASCII (American Standard Code for Information Interchange). Код ASCII содержит 256 символов. Первые 128 символов кода (128=2⁷ ) по семь бит (bit, Binary Digit) каждый (позиции 0 – 127) предназначены для кодирования английского алфавита (строчных и прописных букв) и специальных символов клавиатуры компьютера. Вторая часть кода – оставшиеся 128 символов (позиции 128-257) по одному байту

(byte=8 bit) каждый предназначены для кодирования национальных клавиатур. Коды ASCII хранятся в микросхемах, расположенных на тыльной стороне клавиатуры компьютера. Таким образом, после кодирования информация приобретает числовую форму – это последовательность нулей и единиц (двоичный код). В дальнейшем, перед шифрованием, информацию в зависимости от размера документа, как правило, архивируют (сжимают).

Лекция 2.

Принципы архивирования (сжатия) информации.

- 0 000000 а 1 000001 б 2 000010 в 3 000011 г 4 000100 д 5 000101 е 6 000110 ё 7 000111 ж 8 001000 з 9 001001 и 10 001010 й 11 001011 к 12 001100 л 13 001101 м 14 001110 н 15 001111 о 16 010000 п 17 010001 р 18 010010 с 19 010011 т 20 010100 у 21 010101 ф 22 010110 х 23 010111 ц 24 011000 ч 25 011001 ш 26 011010 щ 27 011011 ъ 28 011100 ы 29 011101 ь 30 011110 э 31 011111 ю 32 100000 я 33 100001

- 0 00000 а 1 00001 б 2 00010 в 3 00011 г 4 00100 д 5 00101 е 6 00110 ё 7 00111 ж 8 01000 з 9 01001 и 10 01010 й 11 01011 к 12 01100 л 13 01101 м 14 01110 н 15 01111 о 16 10000 п 17 10001 р 18 10010 с 19 10011 т 20 10100 у 21 10101 ф 22 10110 х 23 10111 ц 24 11000 ч 25 11001 ш 26 11010 щ 27 11011 ъ 28 11100 ы 29 11101 ь 30 11110 э 31 11111 ю 32 я 33

- 0 00000 а 1 00001 б 2 00010 в 3 00011 г 4 00100 д 5 00101 е 6 00110 ж 7 00111 з 8 01000 и 9 01001 й 10 01010 к 11 01011 л 12 01100 м 13 01101 н 14 01110 о 15 01111 п 16 10000 р 17 10001 с 18 10010 т 19 10011 у 20 10100 ф 21 10101 х 22 10110 ц 23 10111 ч 24 11000 ш 25 11001 щ 26 11010 ъ 27 11 011 ы 28 11100 э 29 11101 ю 30 11110 я 31 11111

Таблица 1. Примеры равномерного кодирования алфавита.

Рассмотрим русский алфавит из 34 символов: 33 литеры плюс пробел и попытаемся экономно его закодировать. Если на каждый символ выделить 6 бит, то как следует из первого столбца табл.1 – это много.

Если закодировать таким способом какой-либо текст, то в нём будут в качестве балласта циркулировать лишние биты. А если на каждый символ выделить 5 бит, то как следует из второго столбца табл.1, этого будет недостаточно. Исключим из алфавита две буквы: ё и ъ.

Тексты в таком алфавите будут читаться без проблем, а на кодирование алфавита достаточно пяти бит на символ (третья строка табл.1) . Таким образом, для оптимального кодирования необходимо,

чтобы кодируемый текст из n символов имел представление

n=2 ^m , где m – число бит на один символ. Такое кодирование называют равномерным. Примером кода с равномерным кодированием может служить рассмотренный выше код ASCII.

Закодированный равномерным кодом текст занимает на носителе информации определённое число бит. Возникает вопрос: нельзя ли это число бит уменьшить без ущерба для прочтения текста, т.е. сжать текст? Оказалось, что можно и эту проблему решил ещё до создания компьютеров американский математик Р. Фано (R.Fano), предложив новую схему кодирования текстов.

Схема двоичного кодирования по Р. Фано (R.Fano)

Идея Р. Фано заключается в применении к алфавиту языка неравномерной схемы кодирования. На те символы (буквы) языка, которые встречаются в текстах чаще, нужно отводить меньше бит, а на те, которые встречаются реже – больше. При этом используется статистика, т.е. частоты (вероятности), с которыми символы встречаются в текстах, написанных на данном языке.

Рассмотрим пример. Пусть для определённости алфавит состоит из 8-ми букв: a, b, c, d, e, f, g, h. При равномерном кодировании достаточно трёх битов на букву, так как 8=2³ .

a  000, b  001, c  010, d  011, e  100, f  101, g  110,

h  111

0 1

0 1 0 1

0 1 0 1

0 1 0 1

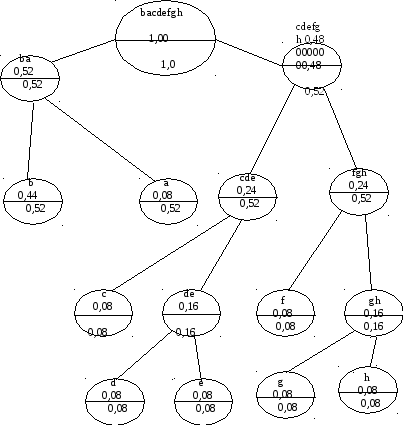
Рис.2 Пример схемы составления кодовых наборов по Р. Фано.

Если учесть частоты (вероятности) встречаемости букв в текстах, то число бит на букву в среднем можно уменьшить, т.е. сделать его меньше трёх. Пусть, например, частоты для определённости будут:

p(a)= 0,08; p(b)= 0,44; p(c) =0,08; p(d)= 0,08; p(e)= 0,08; p(f) =0,08; p(g) =0,08; p(h) =0,08

Заметим, что сумма частот всегда должна быть равна единице (полная система событий).

Схема кода Р. Фано изображена на рис.2. Она основана на следующем алгоритме:

1. составить список букв алфавита в порядке убывания соответствующих им вероятностей.

2. разбить этот список на два подсписка таким образом, чтобы значения вероятностей того, что наугад взятая буква окажется в первом или во втором списке, были бы по возможности равны.

3. приписать одному из списков символ 0, а другому 1.

4. Рассматривая каждый из подсписков как исходный, применить к ним операции 2) и 3).

5. Этот процесс продолжать до тех пор, пока в каждом из очередных подмножеств не окажется по одной букве.

6. Каждой букве приписать двоичный код, состоящий из последовательности нулей и единиц, встречающихся на пути из исходного множества букв, к множеству, состоящему из одной буквы.

В результате получаем двоичные кодовые наборы Фано для символов данного алфавита.

a  01, b  00, c  100, d 1010, e  1011, f  110, g 1110,

h 1111

Среднее число бит на символ алфавита (подсчитывается по правилу вычисления среднего значения случайной величины) получается равным:

0,082+0,442+0,083+0,084+0,084+0,083+0,084+0,084=

24 0,08+0,442=2,8

Это приводит к сжатию текстов в данном примере (по сравнению с равномерным кодированием) на (1-2,8/3)100 %= ~ 7 % .

Таким образом, Р. Фано открыл качественно новую точку зрения на преобразование информации, что послужило основой для поиска других схем кодирования, которые позволяли бы сжимать тексты в ещё большей степени. Такие схемы были предложены американским математиком Д. А. Хаффмэном (1952). Рассмотрим простейшую из них.

Схема двоичного кодирования текстов по Д. А. Хаффмэну (1952)

(D. A. Huffman)

Идея Д. А. Хаффмэна создания кодовых наборов для символов алфавита основана на учёте не только частот отдельных букв

k=1 k=2 k=3 k=4 k=5

b 0,44 b 0,44 b 0,44 b 0,44 b 0,44

a 0,08 (gh) 0,16 (gh) 0,16 (gh) 0,16 (cda) 0,24

c 0,08 a 0,08 (ef) 0,16 (ef) 0,16 -----------

d 0,08 c 0,08 a 0,08 ------------- ₀(gh) 0,16

e 0,08 d 0,08 ------------- ₀(cd) 0,16 ₁(ef) 0,16

f 0,08 ----------- ₀c 0,08 ₁a 0,08

-------- ₀e 0,08 ₁d 0,08

₀g 0,08 ₁f 0,08

₁h 0,08

k=6 k=7 k=8

b 0,44 ------------------ (ghefcdab) 1,00

-------------- ₀(ghefcda) 0,56

₀(ghef) 0,32 ₁b 0,44

₁(cda) 0,24

Таблица 2. Пример схемы для составления двоичного кодового

набора по Д. А. Хаффмэну.

алфавита в текстах, но и частот буквосочетаний.

Алгоритм простейшей схемы кодирования заключается в следующем:

Формируется первый (k=1) столбик, где все буквы алфавита записываются в порядке убывания их вероятностей в тексте, подлежащем кодированию. Напротив каждой буквы пишется соответствующее ей значение частоты (вероятности). Две последние буквы отмечаются двоичными символами 0 и 1.

При известном k – ом столбце строится (k+1) –й столбец по тому же принципу, что и предыдущий, с той лишь разницей, что буквы, отмеченные в предыдущем столбце двоичными символами, в последующем столбце отсутствуют.

В новом столбце их представляет одна составная буква со значением вероятности, равным сумме вероятностей слагаемых букв.

Двоичный кодовый набор каждой буквы строится путём выбора соответствующего ей двоичного символа из последних двух строк каждой таблицы, начиная с конца (в отличие от кода Р. Фано, где двоичные символы считываются при движении из основного множества алфавита к множеству из отдельной буквы).

Рассматривая для сравнения пример из предыдущего параграфа, находим из табл.2, согласно описанному выше алгоритму, кодовые наборы для символов выбранного в качестве примера алфавита.

a  011, b  1, c 0100, d 0101, e  0010, f  0011, g 0000,

h  0001

Среднее число двоичных кодов на один символ алфавита получается равным:

30.08+10.44+40.08+40.08+40.08+40.08+40.08+40.08=270.08+0.44=2.16+0.44=2.6

Это приводит к сжатию текстов на (1-2,6/3)*100 = ~ 13% по сравнению с равномерным кодированием (3 бита на символ в данном примере) и на ~ 6% больше, чем по Р. Фано (2,8 бит на символ, см. предыдущий параграф).

Таким образом, уже из этого простого примера видно, что алгоритм составления кодовых наборов по Д. А. Хаффмэну приводит к большей степени сжатия текстов, чем алгоритм Р. Фано.

Ясно, что далее можно учитывать частоты более сложных буквосочетаний и получать большие степени сжатия текстов. И возникает вопрос: а до какой степени можно сжать и существует ли предел? Этот вопрос был решён американским математиком

К. Шенноном (Shannon C.E., 1945).

О префиксности кодов.

Рассмотрим список кодовых слов (алфавит), использованный в предыдущих примерах,

a, b, c, d, e, f, g, h

со статистикой

p(b)=0,44; p(a)=p(c)=p(d)=p(e)=p(f)=p(g)=p(h) =0,08.

Кодовые наборы по Фано в данном случае имеют вид

a  01, b  00, c  100, d 1010, e  1011, f  110, g 1110,

h 1111,

а по Хаффмэну

a  011, b  1, c 0100, d 0101, e  0010, f  0011, g 0000,

h  0001

Эти кодовые наборы являются неравномерными (не одинаковое число бит на символ) и обращает на себя внимание тот факт, что как в коде Фано, так и в коде Хаффмэна, никакое кодовое слово не является продолжением другого. Такие кодовые наборы (коды) назвали префиксными. Они имеют определённые преимущества при сжатии информации.

Лекция 3.

Сведения из теории информации по К. Шеннону (Shannon C.E., 1945).

По количеству полученных результатов и их практической значимости К. Шеннон по праву считается основоположником теории информации. Рассмотрим некоторые из результатов теории Шеннона.

Шеннон впервые ввёл новое понятие – количество информации. Рассмотрим некоторый алфавит, состоящий из n символов с известными частотами для каждого из символов:

i=n

n = 2 ^m , p _i (i=1, 2, … , n) – частоты символов, p_i =1.

i=1

Количество информации H в таком алфавите Шеннон определил формулой:

i=n

H= - p_i log ₂ p_i

i=1

Количество информации в алфавите, о котором, кроме частот отдельных его символов, известна дополнительная статистика (например, частоты буквосочетаний) будет выражаться более сложной формулой. Доказательство формулы для H, а также более сложные случаи не рассматриваем. Рассмотрим количество информации в алфавите, в котором частоты символов одинаковы (равновероятны). Тогда

n=2^m , p₁= p₂=… = p _n=1/n и H = log ₂ n = log ₂ 2^m = m

Но мы уже знаем, что m – это число бит на символ при равномерном кодировании алфавита. Следовательно, количество информации H имеет смысл числа бит на символ при кодировании. Опираясь на свою формулу для H, Шеннон доказал имеющий важное практическое значение результат:

В любой схеме архивирования (сжатия) текстов получить число бит на символ меньше, чем это следует из формулы Шеннона для H, невозможно.

H(p)

1

0 0.5 1 p

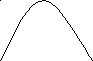
Рис.3. Зависимость H(p) для алфавита из двух бит.

В программных продуктах для архивирования текстов

(например, Win.zip, Win.rar и др.) разработаны и используются

технически более сложные и более эффективные схемы архивирования, но идейная их основа такая же, как и в

рассмотренных выше примерах.

Рассмотрим алфавит из двух символов (битов): 0 и 1. Частоту одного из битов обозначим через p. Тогда из формулы Шеннона получаем, что H есть функция частоты p:

H(p)= - p log ₂ p - (1-p)log ₂ (1-p)

Зависимость H(p) изображена на рис.3. Из этого рисунка видно, что

H(p) достигает максимального значения при p=0,5. Отсюда вытекает следующий практически очень важный результат:

Для наилучшей информативности двоичный код любого текста должен содержать одинаковое число символов 0 и 1 .

Другими словами, для разгрузки двоичного кода любого текста от балластных битов необходимо, чтобы число битов 0 и 1 в нём было

одинаково. Как следует из формулы К. Шеннона это всегда возможно.

Для дальнейшего нам понадобятся некоторые сведения из арифметики.

Необходимые сведения из арифметики.

Приведём без доказательства (для упрощения изложения ) необходимые в дальнейшем факты из арифметики натуральных чисел. Натуральные числа: 1, 2, 3, …, n, … бывают простыми и составными. Простые числа – это числа, которые делятся только на себя и на единицу, например, 1, 2, 3, 5, 7, …. Однако закон распределения простых чисел на числовой оси современной науке не известен. Имеют место теоремы:

Основная теорема арифметики: Всякое натуральное число является произведением простых чисел.

Пусть a, b, p - некоторые натуральные числа. Если разность чисел a и b делится на p без остатка, то числа a и b называют сравнимыми по модулю p. Эту операцию сравнения чисел обозначают при помощи символа сравнения  следующим образом: ab (mod p).

Примеры: 52 (mod 3), 176 (mod 11). Операция сравнения неоднозначна, например, 133 (mod 5) и 138 (mod 5).

Малая теорема Ферма: для любого натурального a и простого p, при условии, что числа a и p не делятся друг на друга

a ^p-1  1 (mod p).

Другая формулировка малой теоремы Ферма утверждает:

При простом p и любом натуральном a

a ^pa (mod p).

Примеры: 2⁵ – 2=30 делится на 5, но 2⁹ – 2=510 не делится на 9, почему?

Числа a и b называются взаимно простыми, если они не имеют общих сомножителей.

Легко проверяется, что a и b при этом не обязательно должны быть простыми.

Функция Эйлера.

Функция Эйлера φ(a) определяется для всех целых положительных a и представляет собою число чисел ряда

0, 1, ..., a-1

взаимно простых с a.

Примеры: φ(1)=1, φ(2)=1, φ(3)=2, φ(4)=2, φ(5)=4, φ(6)=2.

Теорема Эйлера.

φ(m)

При m>1 и a взаимно простом с m a  1 (mod m)

Если p – простое, то φ(p)= p – 1и теорема Ферма вытекает из теоремы Эйлера.

Лекция 4.

1. Защита информации от случайных помех. Код р. Хэмминга.

Рассмотрим некоторый алфавит, в котором n=2 ^m букв. Если буквы появляются в текстах равновероятно, то минимальное количество двоичных символов на одну букву совпадает с H бит на символ и равно m (максимально плотная кодировка). При сбое декодировать такой текст невозможно. Чтобы контролировать ошибки, вводим x дополнительных двоичных позиций под каждую букву. События – ошибок в коде буквы нет, ошибка в первой позиции, ошибка во второй позиции, и так далее, ошибка в позиции m+x – считаем равновероятными. Тогда минимальное количество символов под кодирование одной буквы с контрольными символами x должно определиться количеством информации

H=log₂ (1+m+x).

Но чтобы получить информацию об ошибках после кодирования буквы (или после передачи по каналу связи) нужно иметь информацию в x бит, которая была бы не менее количества информации H:

x  log ₂ (1+m+x).

Из этого неравенства вытекает, что должно быть

2^x – x –1  m.

Например, если x=3, то m можно выбрать равным четырём. Итого имеем семь двоичных позиций под букву, из них четыре позиции – информационные, а три – контрольные. Обозначим эти позиции

b₁ b₂ b₃ b₄ b₅ b₆ b₇

По Р. Хэммингу позиции

b₁ b₂ b₄

нужно выбрать контрольными (мнемоническое правило: номера контрольных позиций это целые степени двойки 0, 1, 2), а позиции b₃ b₅ b₆ b₇ - информационными. Содержимое контрольных позиций должно определяться содержимым информационных позиций. По Р. Хэммингу контрольные позиции заполняются по правилу:

b ₁ = b ₃+b ₅+b ₇ mod 2

b ₂ = b ₃ +b ₆ +b ₇ mod 2 (Х1)

b ₄ = b ₅ +b ₆ +b ₇ mod 2

Тогда (s₁ s₂ s₃) будет двоичным кодом той ячейки, где содержится ошибка, и этот код должен вычисляться по правилу:

s₁ = b ₄ + b ₅ +b ₆ +b ₇ mod 2

s₂ = b ₂ + b ₃ +b ₆ +b ₇ mod 2 (Х2)

s ₃ = b ₁ + b ₃+b ₅+b ₇ mod 2

Если ошибки нет, то (s₁ s₂ s₃)= (0 0 0) .

Если в уравнениях (Х2) заменить символы

b₁ b₂ b₃ b₄ b₅ b₆ b₇

номерами их позиций в двоичной кодировке:

1 (001) 2(010) 3(011) 4(100) 5(101) 6(110) 7(111) ,

то получим, что (s₁ s₂ s₃)= (0 0 0) . В этом случае из уравнений (Х2) вытекают уравнения (Х1) на правило заполнения контрольных позиций.

Пример:

Пусть некоторая буква алфавита имеет код:

b₃ b₅ b₆ b₇ = 1 0 0 1

Находим контрольные символы по формулам (Х1):

b ₁ b ₂ b ₄ = 0 0 1

Тогда расширенная кодировка буквы имеет вид:

b₁ b₂ b₃ b₄ b₅ b₆ b₇ = 0 0 1 1 0 0 1 (X3)

Подсчитываем s₁ , s₂ , s₃ по формулам (Х2) . Получаем, что (s₁ s₂ s₃)= ( 0 0 0 ).

Допустим, что в третьей позиции кода Х(3) возникла по какой-то причине ошибка, и код стал таким:

b₁ b₂ b₃ b₄ b₅ b₆ b₇ = 0 0 0 1 0 0 1 (Х4)

Вычисляем s₁ ,s_2, , s₃ для кода (Х4) по формулам ( Х2). В результате имеем:

s₁ = ( b ₄ + b ₅ +b ₆ +b ₇ mod 2 ) = 0

s₂ = ( b ₂ + b ₃ +b ₆ +b ₇ mod 2 ) = 1

s ₃ = ( b ₁ + b ₃+b ₅+b ₇ mod 2 ) = 1

Получили, что (s₁ s₂ s₃)= (011) – это двоичный адрес третьей ячейки, где возникла ошибка. Таким образом, код Р. Хэмминга позволяет прогнозировать и исправить одиночную ошибку. Код Р. Хэмминга обобщается на произвольные алфавиты и позволяет исправлять не только одиночные ошибки кодов отдельных букв, но и кратные ошибки. Кроме того, дополнительные биты в схеме Р. Хэмминга

используют и для шифрования информации. Это отдельное направление защиты информации, которое мы не рассматриваем.

Из истории криптографии.

История криптографии связана с большим количеством дипломатических и военных тайн и поэтому окутана туманом легенд.

Свой след в истории криптографии оставили многие хорошо известные исторические личности. Приведём наиболее яркие примеры. Первые сведения об использовании шифров в военном деле связаны с именем спартанского полководца Лисандра (шифр “Сцитала”). Цезарь использовал в переписке шифр, который вошёл в историю как шифр “Цезаря”. В более поздние времена шифров было изобретено очень много и мы на них не останавливаемся.

Шифр “Сцитала” известен со времён войны Спарты против Афин в V веке до н. э. Для его реализации использовалась сцитала – жезл, имеющий форму цилиндра. На сциталу виток к витку наматывалась узкая папирусная лента (без просветов и нахлёстов), а затем на этой ленте вдоль оси сциталы записывался открытый текст. Лента разматывалась и получалось (для непосвящённых), что поперёк ленты в беспорядке написаны какие-то буквы. Затем лента отправлялась адресату. Адресат брал такую же сциталу, таким же образом наматывал на неё полученную ленту и читал сообщение вдоль оси сциталы. Отметим, что в этом шифре преобразование открытого текста в зашифрованный заключается в определённой перестановке букв открытого текста. Поэтому класс шифров, к которым относится и шифр «Сцитала», называется шифрами перестановки.

Шифр Цезаря реализует следующее преобразование открытого текста: каждая буква открытого текста заменяется третьей после неё буквой в алфавите, который считается написанным по кругу, т. е. после буквы «z» следует буква «а». Отметим, что Цезарь заменял букву третьей после неё буквой, но можно заменять и какой-нибудь другой. Главное, чтобы тот, кому посылается шифрованное сообщение, знал эту величину сдвига. Класс шифров, к которым относится и шифр Цезаря, называется шифрами замены.

Математические основы шифрования.

Большое влияние на развитие криптографии оказали появившиеся в середине XX века работы американского математика Клода Шеннона. В этих работах были заложены основы теории информации, а также был разработан математический аппарат для исследований во многих областях науки, связанных с информацией.

Принято считать, что теория информации как наука родилась в 1948 году после публикации работы К. Шеннона «Математическая теория связи». В своей работе «Теория связи в секретных системах» Клод Шеннон обобщил накопленный до него опыт разработки шифров.

Оказалось, что даже в очень сложных шифрах в качестве типичных компонентов можно выделить такие простые шифры как шифры замены, шифры перестановки или их сочетания.

Шифр замены.

Легко дать математическое описание шифра замены.

Пусть X и Y – два алфавита (открытого и шифрованного текстов соответственно), состоящие из одинакового числа символов. Пусть также g: X  Y – взаимно однозначное отображение X в Y. Тогда шифр замены действует так: открытый текст

x ₁ x ₂...x _n

преобразуется в шифрованный текст

g ( x )g (x ₂)...g(x _n ).

Шифр перестановки.

Шифр перестановки, как видно из названия, осуществляет преобразование перестановки букв в открытом тексте. Типичным примером шифра перестановки является шифр «Сцитала». Обычно открытый текст разбивается на отрезки равной длины и каждый отрезок шифруется независимо. Пусть, например, длина отрезков равна n и  - взаимнооднозначное отображение множества {1, 2, …,n} в себя. Тогда шифр перестановки действует так: отрезок открытого текста

x ₁ x ₂ ... x _n преобразуется в отрезок шифрованного текста

x , x , …, x .

σ(1) σ(2) σ(n)

Важнейшим для криптографии был результат К. Шеннона о существововании и единственности абсолютно стойкого шифра..