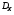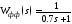Федеральное государственное автономное образовательное учреждение высшего образования "санкт-петербургский национальный исследовательский университет информационных технологий, механики и

ОПТИКИ"

факультет Компьютерных технологий и управления

кафедра Систем управления и информатики

Кафедра

Систем Управления и Информатики

Группа

6147

Расчётно-исследовательская работа

по курсу "Проектирование регуляторов стохастических систем с неопределённостями"

Вариант 31

Автор работы	Чугина Ю. В.	(подпись)
(фамилия, и.о.)
Руководитель	Ушаков А. В.	(подпись)
(фамилия, и.о.)

“

“

20

г.

Санкт-Петербург,

20

14

г.

Работа выполнена с оценкой
Дата защиты “		“		20		г.

Содержание

Расчётно-исследовательская работа 1

2. Синтез закона управления 3

2.1 Переход к векторно-матричному представлению модели объекта управления 3

2.2 Модель экзогенного воздействия 4

2.3 Эталонная модель 5

2.3.1 Полиномиальная динамическая модельная модель 5

2.3.2 Нахождение характеристической частоты 5

2.3.1 Матрицы эталонной модели 5

2.5 Формирование закона управления 6

2.5 Замкнутая система 6

2.6 Проверка требований к спроектированной системе 7

2.6.1 Относительная интервальность 7

2.6.2 Дисперсия выхода системы 7

3 Моделирование 9

3.1 Переход к дискретному описанию системы 9

3.1.1 Шаг дискретизации 9

3.1.2 Дискретная модель формирующего фильтра 9

3.1.3 Генератор дискретного белого шума 9

3.1.3 Дискретная модель замкнутой системы 10

3.2 Результаты моделирования 10

Выводы по работе 11

Литература 12

Непрерывный объект управления (ОУ) с интервальными параметрами задан с помощью передаточной функции (ПФ):

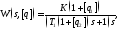
где

Методом медианного модального управления требуется синтезировать закон (ЗУ) вида:

,

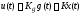где 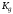- матрица прямой связи по входу;- матрица обратной связи по состоянию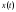,, где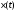– стохастическое стационарное в широком смысле воздействие типа "экспоненциально коррелированный" шум, характеризующийся нулевым математическим ожиданием и дисперсией.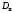

Сигнал 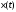считается помехой, которая на выходе системы должна порождать составляющую минимальной величины, т.е. ЗУ должен доставлять системе значение относительной дисперсии выхода системы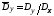, удовлетворяющее условию

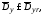(1)

где 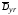– требуемое значение относительной дисперсии выхода.

Функциональное объединение ЗУ и ОУ образует СУ, имеющую векторно-матричное представление:

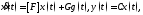
где матрица состояния системы имеет представление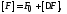и характеризуется оценкой относительной интервальности, значение которой не должно превышать заданного:

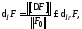(2)

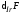где – требуемое значение относительной интервальности матрицы состояния спроектированной системы. В случае невозможности достижения данного условия, требуется оценить влияние угловых реализаций интервальных параметров на значение относительной дисперсии выхода системы.

Числовые значения параметров проектируемой системы, соответствующие варианту задания, приведены в Таблице 1.

Таблица 1 – Исходные данные для варианта 31

1. Значения параметров ПФ ОУ:
K	5
T1	0.05
Δq1	0.1
Δq2	0.1
2.Значение дисперсии	10
3.Формирующий фильтр «окрашенного шума» с передаточной функцией
Внешнее стохастическое воздействие типа «окрашенный шум»	сигнал помехи
Значение требуемой относительной дисперсии выхода	0.0044
Относительная интервальность матрицы состояния системы	0.02