Контрольная работа № 2

_{В ЗАДАЧАХ 91-100 найти неопределённые интегралы способом подстановки}

_{(методом замены переменной).}

_{91. . 92.}

_{93. 94.}

_{95. 96.}

_{97. 98.}

_{99. 100.}

В ЗАДАЧАХ 101-110 найти неопределённые интегралы применяя метод интегрирования по частям.

_{101. 102.}

_{103. 104.}

_{105. 106.}

_{107. 108.}

_{109. 110.}

В ЗАДАЧАХ 111-120 найти неопределённые интегралы, пользуясь разложением рациональных дробей на простейшие.

_{111. 112.}

_{113. 114.}

_{115. 116.}

_{117. 118.}

_{119. 120.}

В ЗАДАЧАХ 121-130 вычислить определённые интегралы.

_{121. 122.}

_{123. 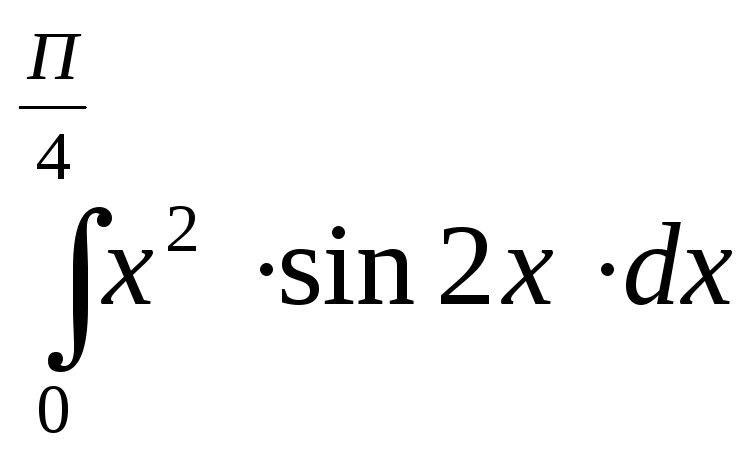124.}

_{125. 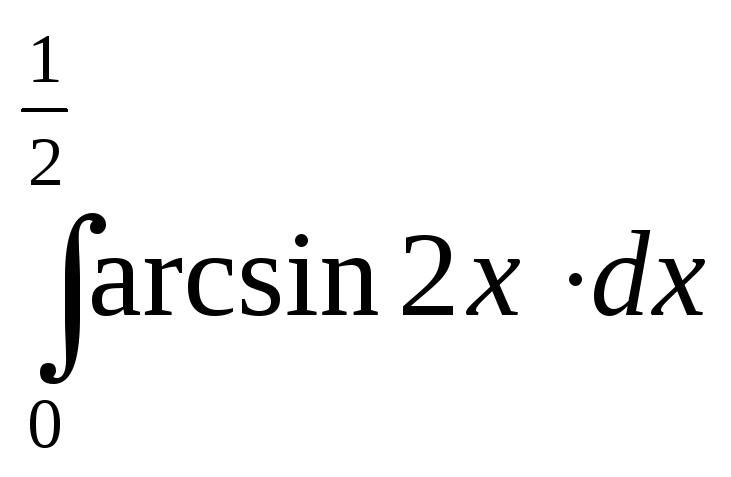126.}

_{127. 128.}

_{129. 130.}

В ЗАДАЧАХ 131-140 вычислить площадь, ограниченную заданными параболами.

_131.

_132.

_133.

_134.

_135.

_136.

_137.

_138.

_139.

_140.

В ЗАДАЧАХ 141-150 найти длину дуги кривой.

_{141. 142.}

_{143. 144.}

_{145. 146.}

_{147. 148. y =lnx,}

_{149. 150.}

_{В ЗАДАЧАХ 151-160 вычислить несобственные интегралы и установить их расходимость.}

_{151. 152.}

_{153. 154.}

_{155. 156.}

_{157. 158.}

_{159. 160.}

В ЗАДАЧАХ 161-210 вычислить частные производные первого и второго порядков от заданных функций.

_{161. 162.}

_{163. 164.}

_{165. 166.}

_{167. 168.}

_{169. 170.}

_{В ЗАДАЧАХ 171-180 задана функция z = f (x,y). Найти градиент и производную этой функции в заданной точке M (x0, y0) в направлении вектора составляющего угол  с положительным направлением оси OX.}

_171.

_172.

_{173. M (2,2),}

_174.

_175.

_{176. z =ln (x}²_+y²_{), M (3,4),}

_{177. M (1,-2),}

_178.

_{179. M (1,1),}

_{180. M (2,2),}

В ЗАДАЧАХ 181-190 найти экстремум заданной функции.

_{181. 182.}

_{183. 184.}

_{185. 186.}

_{187. 188.}

_{189. 190.}

В ЗАДАЧАХ 191-200 с помощью двойного интеграла вычислить координаты центра тяжести фигуры, ограниченной заданными линиями (поверхностную плотность считать равной единице).

_{191. -x+2y = 1 192.}

_{193. 3x - 4y =1 194. x}²_+y² _=9;

_{195. 196. x-5y =1.}

_{197. x-3y-3 =0. 198. 2x-5y-1 =0.}

_{199. 200. x+y+2=0.}

_{В ЗАДАЧАХ 201-210 вычислить работу, совершаемую переменной силой на криволинейном пути L, соединяющем заданные точки M и N.}

_{201.L-дуга параболы y =x}²_{+2x;M (0;0),N (1;3)}

_{202.L- дуга параболы y =2x}²_{+1;M (0;1), N (2;9)}

_{203.L-дуга кубической параболыy=x}³_{;M (0;0),}

_{N (2;8).}

_{204.L- дуга параболы y =7x}²_{+2x; M (0;0),}

_{N (2;32)}

_{205.L- отрезок прямой, соединяющий точки}

_{M (1;2) и N (3;5)}

_{206.L- дуга параболы y =3x}²_{+x; M (1;4),}

_{N (3;30).}

_{207.L- дуга кубической параболы y=x}³_+1;

_{M (0;1), N (1;2).}

_{208.L-дуга кубической параболы y=x}³_+2;

_{M (1;3), N (2;10).}

_{209.L- дуга параболы y =x}²_{+x; M (1;2), N (3;12).}

_{210.L- дуга параболы y =3x}²_{+2; M (2;14),}

_{N (3;29).}

ПРИЛОЖЕНИЕ

Таблица 1