Лекция №7 Движение тела переменной массы. Уравнение Мещерского и Циолковского.

В природе и современной технике мы нередко сталкиваемся с движением тел, масса которых меняется со временем. Масса Земли возрастает вследствие падения на нее метеоритов, масса метеорита при полете в атмосфере уменьшается в результате отрыва или сго­рания его частиц, масса дрейфующей льдины возрастает при намер­зании и убывает при таянии и т. д. Движение якоря с якорной цепью, когда все большее число звеньев цепи сходит с лебедки,— пример движения тела переменной массы. Ракеты всех систем, реактивные самолеты, реактивные снаряды и мины также являются телами, масса которых изменяется во время движения.

Общие законы динамики тел с переменной массой были открыты и исследованы И. В. Мещерским и К. Э. Циолковским. Циолков­ским были разработаны фундаментальные проблемы реактивной техники, которые в наши дни служат основой для штурма человеком межпланетных пространств.

Для вывода основного уравнения движения тела переменной массы рассмотрим конкретный случай движения простейшей ра­кеты (рис. 4).

Мы будем рассматривать ракету как достаточно малое тело, положение центра тяжести которого не меняется по мере сгорания пороха. В этом случае мы можем считать ракету материальной точ­кой переменной массы, совпадающей с центром тяжести ракеты.

Не рассматривая физико-химическую природу сил, возникаю­щих при отбрасывании от ракеты газов, образованных при сго­рании пороха, сделаем такое упрощающее вывод предположение: будем считать, что отбрасываемая от ракеты частица газа dM взаимодействует с ракетой М только в момент их непосредственного контакта. Как только частица dM приобретает скорость относитель­но точки М, ее воздействие на нее прекращается. Предположим далее, что изменение массы ракеты М происходит непрерывно, без скачков. (Это значит, что мы не рассматриваем многоступен­чатые ракеты, масса которых меняется скачкообразно.) Это пред­положение позволяет считать, что существует производная от мас­сы по времени.

Пусть в момент t масса ракеты М, а ее скорость относительно неподвижной системы координат(рис. 5). Положим, за время dt от ракеты отделилась частица массы (—dM) со скоростью (относи­тельно той же неподвижной системы координат), равной и. Знак «минус» перед приращением массы указывает на то, что приращений это отрицательное, масса ракеты убывает.

Положим, равнодействующая внешних сил, действующих на ракету (силы тяжести и сопротивления среды), F. Как сказано выше, в момент отделения частицы массы (—dM) между ней и ра­кетой действует неизвестная нам реактивная сила Fp. Сила Fp для системы ракета — частица является внутренней. Чтобы исключить

ее из рассмотрения, воспользуемся законом изменения количества движения. Количество движения системы ракета — частица в момент t , т. е. перед отделением частицы:

Количество движения системы в момент t+dt (после отделения частицы) складывается из количества движения массы [М—(—dM)], получившей скорость (), и количества движения массы частицы — dM, летящей со скоростью :

(20)

Изменение количества движения системы за время dt:

Величина dP должна быть приравнена импульсу равнодействующей внешних сил

(21)

Отсюда, перегруппировав члены и разделив на dt, получим ос­новное уравнение движения точки переменной массы:

(22)

Это уравнение иначе называют уравнением Мещерского. Для ракеты <0, так как при полете масса ее убывает. Если масса тела во время движения увеличивается, то> 0. При=0 уравнение (22) переходит в уравнение второго закона Нью­тона для случая постоянной массы.. Величина u —есть скорость выбрасываемых ракетой частиц относительно системы координат, движущейся с ракетой. Эту скорость называют обычно просто относительной скоростью V. Тогда равенство (22) запишется в виде

(23)

Для любого момента времени произведение массы те­ла на его ускорение равно векторной сумме равнодействующей приложенных к телу внешних сил и реак­тивной силы. При движении ракеты вблизи Земли равнодействую­щая внешних сил представляет собой сумму силы тяжести и силы сопротивления воздуха. Ускорение ракеты зависит еще и от реактивной силы, изменяя величину и направление которой мож­но управлять полетом ракеты.

Если относительная скорость отбрасываемых частиц равна 0, то следует

M

Важный вклад в механику тел переменной массы применительно к конкретным задачам реактивной техники внесен знаменитым рус­ским ученым Константином Эдуардовичем Циолковским. В 1903 г. была издана его работа «Исследование мировых пространств ре­активными приборами», в которой К. Э. Циолковский исследовал ряд случаев прямолинейных движений ракет. К. Э. Циолковским обоснована и доказана возможность практического использования реактивного движения. Им найдены условия, при которых можно получить скорости, достаточные для осуществления космического полета. Полученная им формула, связывающая скорость ракеты с ее начальной массой, до сих пор используется для предваритель­ных расчетов. В работах 1911—1914 гг. он изучил вопрос о вели­чине запасов топлива, необходимых для преодоления сил тяготения Земли, и предложил высококалорийное топливо, позволяющее получить большие скорости истечения газовых струй. К. Э. Циол­ковского по праву считают изобретателем жидкостных ракет даль­него действия и основоположником теории межпланетных полетов.

Ему принадлежит идея разработки теории так называемых многоступенчатых ракет, когда на некоторых интервалах времени масса ракеты меняется непрерывно, а в некоторые моменты — скачком.

Им проведены большие исследования по оценке сил сопро­тивления при движении тел переменной массы. К. Э. Циолковским поставлен целый ряд оригинальных проблем, имеющих решающее значение для развития реактивной техники.

Для того чтобы выяснить основные факторы, создающие воз­можность реактивного движения с большими скоростями, рас­смотрим движение точки переменной массы в безвоздушном про­странстве (отсутствует сопротивление движению тела), без действия внешних сил (силы тяготения). Предположим, что скорость исте­чения частиц направлена прямо противоположно вектору скорости

тела . Эти условия соответствуют так называемой первой задаче Циолковского. В результате получаем формулу Циолковского и следствие из нее. Найдем при сделанных предположениях скорость движения тела (точки) и закон ее движения.

При сформулированных условиях уравнение движения приобре­тает вид:

M (25) или

(26)

Положим, M=Mof(t), где f(t)— функция, определяющая закон изменения массы.)=1. Подставив в (26) значение М и проинтегрировав, получим:

Для определения постоянной С учтем, что при t==0 f(0)=1 и, тогда C=и

(27)

Эта формула носит название формулы Циолковского. Из формулы следует, что скорость, приобретенная точкой переменной массы, зависит от относительной скорости V и отношения начальной массы к остающейся к концу процесса горения. Если масса точки в конце процесса горения M, а отброшенная масса (масса топлива)—m, то при нулевой начальной скорости получаем для расчета скорости в конце процесса горения выражение:

Отношение называют числом Циолковского. Для современ­ных ракет можно положитьV=2000 м/сек. Тогда при числе Циол­ковского Z=0,250; 9,000; 32,333; 999,000 получим соответственноcкорости=446; 4605; 7013; 13 815 м/сек. Из формулы Циолковcкого (27) следует, что:

1) скорость точки переменной массы в конце активного участка тем больше, чем больше скорость отбрасывания частиц;

2) скорость в конце активного участка тем больше, чем больше скорость отбрасывания частиц число Циолковского;

3)скорость точки переменной массы в конце активного участка не зависит от закона изменения массы (режима горения). Задан­ному числу Циолковского соответствует определенная скорость точки в конце процесса горения независимо от того, быстро или медленно шло горение. Это следствие является проявлением за­кона сохранения количества движения;

4)для получения возможно больших скоростей точки перемен­ной массы в конце активного участка выгоднее идти по пути уве­личения относительной скорости отбрасывания частиц, чем по пути увеличения запасов топлива.

Из уравнения (27) можно найти закон изменения расстояния излучающей точки от начала координат; полагая V=const, полчим:

(28)

после интегрирования:

s=s+t-V(29)

Отсюда следует, что закон расстояния в отличие от закона скорости зависит от закона изменения массы, т. е. от функции f(t).

Лекция № 8. Работа силы, мощность энергия. Консервативные и неконсервативные силы и системы. Независимость работы консервативной силы от траектории. Кинетическая энергия. Потенциальная энергии. Связь силы с потенциальной энергией. Закон сохранения механической энергии в консервативной системе. Внутренняя энергия. Закон сохранения энергии в неконсервативной системе. Применение законов сохранения импульса и энергии при анализе упругих и неупругих ударов.

Если под действием некоторой силы тело совершает элементарное перемещение, то говорят, что сила совершает элементарную работу(рис. 1). Вектор силы можно разложить на две составляющие, одна из которыхсовпадает по направлению с вектором перемещения, другаяперпендикулярна ему.

Очевидно, что перемещать тело, а, следовательно, совершать работу будет только составляющая силы . Таким образом, элементарная работа

, (1)

где – угол между вектором силы и элементарным перемещением.

Так как скалярное произведение двух векторов равно произведению их модулей на косинус угла между ними, то

. (2)

Для того чтобы определить работу по всей траектории движения, необходимо просуммировать работы на каждом элементарном участке

. (3)

Единицей работы в СИ служит работа, совершаемая на пути в один метр с силой в один ньютон, действующей в направлении перемещения. Эта единица называется джоулем (Дж), т.е. 1 Дж = 1 Н1 м.

Заметим, что в джоулях измеряется также энергия , количество теплоты.

Работа, совершаемая в единицу времени, называется мощностью:

. (4)

Единицей мощности в СИ является ватт (Вт) – это такая мощность, при которой за одну секунду совершается работа, равная одному джоулю, т. е. 1 Вт = 1 Дж/1с. Заметим, что 1 кВт = 10³Вт, 1 МВт = 10⁶Вт, 1 ГВт = 10⁹Вт (приставка М читается как «мега», а приставка Г – как «гига»). В технике иногда применяется единица мощности, именуемая лошадиной силой (л. с.) и равная 736 Вт.

Все силы, встречающиеся в механике , принято разделять на консервативные и неконсервативные.

Сила, действующая на материальную точку, называется консервативной (потенциальной), если работа этой силы зависит только от начального и конечного положений точки. Работа консервативной силы не зависит ни от вида траектории, ни от закона движения материальной точки по траектории (см. рис. 2): .

Изменение направления движения точки вдоль малого участка на противоположное вызывает изменение знака элементарной работы , следовательно,. Поэтому работа консервативной силы вдоль замкнутой траектории 1a2b1 равна нулю: .

Точки 1и 2, а также участки замкнутой траектории 1a2 и 2b1 можно выбирать совершенно произвольно. Таким образом, работа консервативной силы по произвольной замкнутой траектории L точки ее приложения равна нулю:

или . (5)

В этой формуле кружок на знаке интеграла показывает, что интегрирование производится по замкнутой траектории. Часто замкнутую траекторию L называют замкнутым контуром L (рис. 3). Обычно задаются направлением обхода контура L по ходу часовой стрелки. Направление элементарного вектора перемещения совпадает с направлением обхода контураL. В этом случае формула (5) утверждает: циркуляция вектора по замкнутому контуруL равна нулю.

Следует отметить, что силы тяготения и упругости являются консервативными, а силы трения неконсервативными. В самом деле, поскольку сила трения направлена в сторону, противоположную перемещению или скорости, то работа сил трения по замкнутому пути всегда отрицательна и, следовательно, не равна нулю.

Если на материальную точку действует консервативная сила, то можно ввести скалярную функцию координат точки, называемую потенциальной энергией.

Потенциальную энергию определим следующим образом

, (6)

где С– произвольная постоянная, а– работа консервативной силы при перемещении материальной точки из положения в фиксированное положение. Образуем разность значений потенциальной энергии для точек 1 и 2 (см. рис. 4) и воспользуемся тем, что

.

Правая часть, полученного соотношения, дает работу, совершаемую на пути из точки 1

1

в точку 2, проходящем через точку О; Вследствие независимости работы от формы пути такая же работа А совершается на любом другом пути, т.е.

О

. (7)

С

Рис. 3

ледовательно, работа консервативных сил равна разности значений функцииW_n в начальной и конечной точках пути, т.е. убыли потенциальной энергии.

Потенциальная энергия определяется с точностью до постоянной. Однако, это не имеет существенного значения, поскольку во все физические соотношения входит либо разность значений потенциальной энергии, либо ее производная по координатам.

Рассмотрим систему, состоящую из многих материальных точек. Если задано положение каждой материальной точки, то этим определено и положение всей системы или ее конфигурация. Если силы, действующие на материальные точки системы, зависят только от конфигурации системы (т.е. только от координат материальных точек) и сумма работ этих сил при перемещении системы из одного положения в другое не зависит от пути перехода, а определяется только начальной и конечной конфигурациями системы, то такие силы называются консервативными. В этом случае для системы материальных точек также можно ввести понятие потенциальной энергии системы, обладающей свойством (7): , (8)

где - полная работа консервативных сил, действующих на материальные точки системы при переходе ее из конфигурации 1 в конфигурацию 2; и - значения потенциальной энергии системы в этих конфигурациях.

Связь между силой, действующей на тело в данной точке поля, и его потенциальной энергией определяется по следующим формулам:

(9)

или , (10)

где – называется градиентом скалярной функции;– единичные векторы координатных осей;

. (11)

Часто формулу (9) записывают также в виде , где– оператор набла, определяемый по формуле (11).

Обозначим через храстяжение пружины, т.е. разность длин пружины в деформированном и недеформированном состояниях.

При возвращении пружины из деформированного состояния в недеформированное сила совершает работу.

. (12)

Таким образом, потенциальная энергия упруго деформированной пружины

. (13)

На рис. 5 изображены две материальные точки массы m₁иm₂. Положение их характеризуется радиусами-векторамиисоответственно. Элементарная работа, совершаемая силами гравитационного притяжения этих точек, где– сила, действующая на первую материальную точку со стороны второй, а– сила, действующая на вторую материальную точку со стороны первой; согласно 3-му закону Ньютона=-;и– элементарные перемещения материальных точек. С учетом этого, где. Учитывая, чтоипротивоположно направлены и что величина, находим. Полная работа

, (14)

где R₁иR₂– начальное и конечное расстояние между материальными точками.

Эта работа равна изменению потенциальной энергии A=W_n1 -W_n2. Учитывая (14), находим, что потенциальная энергия гравитационного притяжения двух материальных точек

или(15)

где R или r – расстояние между материальными точками.

Формула (15) справедлива также для однородных сферических тел; в этом случае r– расстояние между центрами масс таких тел. В частности, потенциальная энергия тела массыт, находящегося в поле гравитации Земли, масса которойМ,

(16)

Изменение потенциальной энергии тела массы m, поднятого с поверхности Земли (r = R, гдеR– радиус Земли) на высотуh (r = R + h), согласно (16), равно:

(17)

Если h<<R, то в знаменателе формулы (17) можно пренебречь слагаемымhи она перейдет в известную формулу

или , (18)

если потенциальную энергию на поверхности Земли принять равной нулю,где – ускорение силы тяжести на поверхности Земли. Таким образом, формула (18) была получена в предположении, что сила тяжести (и ускорение силы тяжести) не изменяются с высотойh, т.е. поле силы тяжести Земли однородно. Поэтому формула (18) является приближенной формулой, в отличие от строгой формулы (16).

Напишем уравнение движения материальной точки (частицы) массы m, движущейся под действием сил, результирующая которых равна: .

Умножим скалярно правую и левую часть этого равенства на элементарное перемещение точки , тогда

. (1)

Так как , то легко показать, чтоИспользуя последнее равенство и то обстоятельство, что масса материальной точки постоянная величина, преобразуем (1) к виду.

Проинтегрировав части этого равенства вдоль траектории частицы от точки 1 до точки 2, имеем:

.

Согласно определению первообразной и формуле (4.3) для работы переменной силы, получим соотношение: .

Величина

(2)

называется кинетической энергией материальной точки.

Таким образом мы приходим к формуле

, (3)

из которой следует, что работа результирующей всех сил, действующих на материальную точку, расходуется на приращение кинетической энергии этой частицы.

Полученный результат без труда обобщается на случай произвольной системы материальных точек.

Кинетической энергией системы называется сумма кинетических энергий материальных точек, из которых эта система состоит или на которые ее можно мысленно разделить: .

Напишем соотношение (3) для каждой материальной точки системы, а затем все такие соотношения сложим. В результате снова получим формулу, аналогичную (3), но для системы материальных точек.

, (4)

где и– кинетические энергии системы, а поднеобходимо понимать сумму работ всех сил, действующих на материальные точки системы.

Таким образом мы доказали теорему (4): работа всех сил, действующих на систему материальных точек, равна приращению кинетической энергии этой системы.

Рассмотрим систему из n материальных точек, на которые действуют как консервативные так и неконсервативные силы. Найдем работу, которую совершают эти силы при перемещении системы из одной конфигурации в другую. Работа консервативных сил может быть представлена как убыль потенциальной энергии системы[(см. 4.8)]:

.

Работу неконсервативных сил обозначим посредством А*. Согласно (4) суммарная работа всех сил затрачивается на приращение кинетической энергии системы, следовательно,или

.

Сумма кинетической и потенциальной энергии представляет собой полную механическую энергию Е системы:

. (5)

Таким образом

. (6)

Очевидно, что если неконсервативные силы в системе отсутствуют, т.е. , то ее полная механическая энергия остается постоянной (сохраняется) т.е. Е = const. Эту теорему называют законом сохранения механической энергии, он утверждает:полная механическая энергия системы материальных точек, находящихся под действием консервативных сил остается постоянной.

В такой системе могут происходить лишь превращения потенциальной энергии в кинетическую и обратно, но полный запас энергии системы измениться не может. При наличии неконсервативных сил (например, сил трения, сил сопротивления...) механическая энергия системы не сохраняется, она уменьшается, что приводит к ее нагреванию. Такой процесс называется диссипацией (рассеянием) энергии. Силы, приводящие к диссипации энергии, называются диссипативными.

При соударении тел они в большей либо меньшей мере деформируются. При этом кинетическая энергия тел частично или полностью переходит в потенциальную энергию упругой деформации и во внутреннюю энергию тел. Увеличение внутренней энергии приводит к нагреванию тел.

Ограничимся рассмотрением центрального ударадвух шаров, при котором шары движутся вдоль прямой, проходящей через их центры.На рис. 1 изображены два возможных случая центрального удара.

Рассмотрим два предельных вида соударения – абсолютно неупругий и абсолютно упругий удары.

Интересным примером, где имеет место потеря механической энергии под действием диссипативных сил, является абсолютно неупругий удар, при котором потенциальная энергия упругой деформации не возникает; кинетическая энергия тел частично или полностью превращается во внутреннюю энергию. После такого удара тела движутся с одинаковыми скоростями (т.е. как одно тело) либо покоятся.

При абсолютно неупругом ударе выполняется только закон сохранения суммарного импульса тел: , откуда,

. (7)

Кинетическая же энергия, которой обладала система до удара, после соударения уменьшается или стремится к нулю. Изменение кинетической энергии:

.(8)

Это такой удар, при котором полная механическая энергия тел сохраняется. Сначала кинетическая энергия частично или полностью переходит в потенциальную энергию упругой деформации. Затем тела возвращаются к первоначальной форме, отталкиваясь друг от друга. В итоге потенциальная энергия упругой деформации снова переходит в кинетическую и тела разлетаются со скоростями, которые определяются исходя их законов сохранения суммарного импульса и суммарной энергии тел.

Обозначим массы шаров m₁ и m₂, скорости шаров до удара и, скорости шаров после удараии напишем уравнения сохранения импульса и энергии:

(9)

Решая совместно эти два уравнения, найдем скорости шаров после абсолютно упругого удара:

(10)

Чтобы осуществить расчеты, нужно спроектировать все векторы на ось х. Сделаем это, например, для случая а) на рис. 1:

. (11)

Если ответ получается положительным, то это означает, что шар после соударения движется вправо, если – отрицательный, то шар движется влево.

Классическая механика учитывает только кинетическую энергию макроскопического движения тел и их макроскопических частей, а также их потенциальную энергию. Но она полностью отвлекается от внутреннего атомистического строения вещества. При ударе, трении и аналогичных процессах кинетическая энергия видимого движения тел не пропадает. Она только переходит в кинетическую энергию невидимого беспорядочного движения атомов и молекул вещества, а также в потенциальную энергию их взаимодействия. Эта часть энергии получила название внутренней энергии.

Беспорядочное движение атомов и молекул воспринимается нашими органами чувств в виде тепла.

Таково физическое объяснение кажущейся потери механической энергии при ударе, трении и пр.

В физике закон сохранения энергии распространяют не только на явления, рассматриваемые в механике, но на все без исключения процессы, происходящие в природе.

Полное количество энергии в изолированной системе тел и полей всегда остается постоянным; энергия лишь может переходить из одной формы в другую.

В основе закона сохранения энергии лежит такое свойство времени как однородность, т.е. равнозначность всех моментов времени, заключающаяся в том, что замена момента времени t₁моментом времениt₂, без изменения значений координат и скоростей тел не изменяет механических свойств системы. Поведение системы, начиная с момента времениt₂будет таким же, каким оно было бы, начиная с моментаt₁.

Лекция № 9.

Твердое тело как система материальных точек. Абсолютно твердое тело. Поступательное и вращательное движение абсолютно твердого тела. Мгновенные оси вращения. Момент силы. Момент инерции. Уравнение динамики вращательного движения тела относительно неподвижной оси.

Абсолютно твеpдым телом называется тело, дефоpмациями котоpого по условиям задачи можно пpенебpечь. У абсолютно твеpдого тела pасстояние между любыми его точками с течением вpемени не меняется. В теpмодинамическом смысле такое тело не обязательно должно быть твеpдым.  Напpимеp, легкий pезиновый шаpик, наполненный водоpодом, можно pассматpивать как абсолютно твеpдое тело, если нас интеpесует его движение в атмосфеpе. Положение абсолютно твеpдого тела в пpостpанстве хаpактеpизуется шестью кооpдинатами. Это видно из следующих сообpажений. Положение абсолютно твеpдого тела полностью фиксиpуется заданием тpех точек, жестко связанных с телом. Положение тpех точек задается девятью кооpдинатами, но поскольку pасстояния между точками неизменны, то эти девять кооpдинат будут связаны тpемя уpавнениями. Следовательно, независимых кооpдинат, опpеделяющих положение твеpдого тела в пpостpанстве, останется шесть. Числу независимых кооpдинат соответствует число независимых видов движения, на котоpые может быть pазложено пpоизвольное движение тела. У абсолютно твердого тела таких движений шесть. Говоpят, что абсолютно твеpдое тело обладает шестью степенями свободы. Независимые виды движения тела можно выбpать по-pазному. Напpимеp, поступим следующим обpазом. Свяжем с твеpдым телом "жестко" одну точку и будем следить за ее движением и за движением тела вокpуг этой точки. Движение одной точки описывается тpемя кооpдинатами, т.е включает в себя тpи степени свободы. Их называют поступательными степенями свободы. Тpи дpугие степени свободы пpиходятся на вpащательное движение тела вокpуг выбpанной точки. Соответствующие степени свободы называются вpащательными.Таким обpазом, пpоизвольное движение твеpдого тела может быть pазбито на поступательное и вpащательное вокpуг неподвижной точки. Ниже мы pассмотpим поступательное движение твеpдого тела и его вpащательное движение вокpуг неподвижной оси.Поступательным движениемтела называется такое движение, пpи котоpом любая пpямая, жестко связанная с телом, пеpемещается паpаллельно самой себе.         Пpимеpом такого движения может служить движение велосипедной педали пpи движении велосипедиста. Пpи поступательном движении все точки тела движутся совеpшенно одинаково: у них одинаковые, но смещенные относительно дpуг дpуга тpаектоpии, одинаковые в любой момент вpемени скоpости, одинаковые ускоpения. Если так, то поступательное движение абсолютно твеpдого тела эквивалентно движению одной точки и кинематика поступательного движения сводится к кинематике точки.        Вpащательное движение тела вокpуг неподвижной оси. Положение абсолютно твеpдого тела в этом случае хаpактеpизуется одной единственной кооpдинатой: углом повоpота тела вокpуг оси. Угол отсчитывается от некотоpого положения тела в опpеделенную стоpону, в pезультате этого углу повоpота пpиписывается знак (pис. 1.5).

Важнейшей хаpактеpистикой движения тела в этом случае является угловая скоpость. Угловой скоpостью тела называется пеpвая пpоизводная от угла повоpота по вpемени: (1.)         Угловая скоpость показывает, на какой угол повоpачивается тело в секунду.Угловая скоpость хаpактеpизуется знаком. Она меньше нуля, если угол меняется в напpавлении, обpатном положительному напpавлению его отсчета.         Если тело вpащается в одну стоpону, то его движение иногда описываетсячислом обоpотов N. Число обоpотов N связано с углом повоpота фоpмулой(2)         В этом случае вместо угловой скоpости вводят понятие частоты вpащения (число обоpотов в секунду). Частота вpащения pавна пеpвой пpоизводной от числа обоpотов по вpемени, т. е.(3)         Если вpащение pавномеpное, то угловую скоpость можно опpеделить известной фоpмулой:(4)         Но эта фоpмула невеpна, если вpащение ускоpенное и угловая скоpость изменяется во вpемени.         Угловым ускоpением называется пеpвая пpоизводная угловой скоpости по вpемени (или втоpая пpоизводная от угла повоpота по вpемени).(5)         Вpащение является ускоpенным (с наpастающей угловой скоpостью), если знаки угловой скоpости и углового ускоpения одинаковы, и замедленным, если знаки угловой скоpости и углового ускоpения pазные.         Пpи вpащении твеpдого тела вокpуг неподвижной оси все точки тела движутся по окpужностям с центpами, pасположенными на оси вpащения. Линейные величины для точек вpащающегося твеpдого тела связаны с угловыми, т.к. во все фоpмулы этих соотношений будет входить pадиус вpащения точки.        Спpаведливы следующие соотношения:

(6)         Между движением твеpдого тела вокpуг неподвижной оси и движением отдельной матеpиальной точки (или поступательным движением тела) существует тесная и далеко идущая аналогия. Пpи pешении задач полезно пользоваться этой аналогией. Каждой линейной величине из кинематики точки соответствует подобная величина из кинематики вpащения твеpдого тела. Кооpдинате s соответствует угол , линейной скоpости v - угловая скоpость,   линейному (касательному) ускоpению а - угловое ускоpение .         Пpиведем пpимеp того, как можно пользоваться аналогией между поступательным и вpащательным движениями. Известно, что pавноускоpенное движение описывается фоpмулами: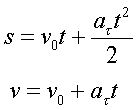

                                                                                                                            (7)         По аналогии можно записать соответствующие фоpмулы для pавноускоpенного вpащения твеpдого тела:

(8)         Аналогия между поступательным и вpащательным движениями существует и в динамике.

Движение абсолютно твердого тела можно рассматривать как движение системы большого числа материальных точек, сохраняющих неизменное положение друг относительно друга. Для каждой материальной точки справедлив второй закон динамики. Если масса -й точки і скорость её , то

, (9)

где — внутренние силы, действующие на данную точку со стороны других точек тела, а— действующие на неё внешние силы.

Напишем уравнения, аналогичные уравнению (1) , для каждой точки и просуммируем их. Так как , то

, (10)

или

, (11)

т.е. производная от полного количества движения тела равна сумме внешних сил, действующих на тело.

Равенство (2) можно записать в виде

. (12)

Если тело движется только поступательно, то ускорения всех его точек одинаковы и, учитывая, что (масса тела ), получим

, (13)

где

.

Уравнение (5) носит название уравнения поступательного движения твердого тела.

Линия, соединяющая точки тела, которые в данный момент остаются в покое, называется мгновенной осью вращения. Качение может быть представлено как вращение вокруг мгновенных осей вращения. Мгновенная ось вращения перемещается по боковой поверхности цилиндра со скоростью, равной скорости поступательного движения его оси.

Рассмотрим движение шарика массой , укрепленного на легкой нити, по окружности радиусав вертикальной плоскости. При длине нити, значительно большей радиуса шарика, его можно рассматривать как материальную точку.

Шарик движется под действием двух сил: силы упругости, действующей со стороны деформированной нити, и силы тяжести. Первая направлена все время вдоль радиуса окружности, а вторая составляет с ним переменный угол. Направление и величина результирующей этих сил меняется во время движения, поэтому меняется ускорение, с которым движется шарик.

Рассмотрим движение шарика на малом участке окружности, в пределах которого силу можно считать постоянной по величине и направлению. Обозначим угол между результирующей сил, действующей на шарик, и направлением касательной к траектории через (рис .1).

рис №1. Обращение точки по окружности под действием силы .

Шарик приобретает тангенциальное ускорение под действием тангенциальной составляющей силы, равной

.

По второму закону динамики

.

Как известно, угловое ускорение и , следовательно,

. (14)

Умножая обе части равенства на , получим :

(15)

Слева в равенстве стоит величина , которая носит название момента силы относительно центра вращения.

Момент силы М относительно центра вращения численно равен произведению силы на длину перпендикуляра, опущенного из центра вращения на направление силы. Величина называется плечом. Поэтому иногда момент силы определяют как произведение силы на плечо.

Величина называется моментом инерции.

Момент инерции материальной точки относительно центра вращения численно равен произведению массы точки на квадрат её расстояния от центра вращения.

Таким образом, (16)

Равенство свидетельствует о том, что инерциальные свойства материальной точки при движении по окружности определяет не только величина массы точки, но и её положение относительно центра вращения. Угловое ускорение — величина векторная, момент инерции — величина скалярная. Следовательно, момент силы — величина векторная и совпадает по направлению с вектором углового ускорения.

Положим, твердое тело может без трения вращаться вокруг неподвижной оси ОО

(рис №2 ).

рис.№2. Тело, вращающееся вокруг неподвижной оси.

Пусть к телу приложена результирующая внешних сил . Кроме неё на тело действуют силы реакции со стороны связей (подшипников). Если силы трения отсутствуют, то силы реакции связей проходят через ось вращения и момент их относительно оси равен нулю. Подсчитаем момент равнодействующей внешних сил относительно оси вращения.

Для этого расчленим тело на достаточно малые элементы, чтобы расстояния от всех точек отдельного элемента до оси можно было считать одинаковым. Пусть масса элемента —, внешняя сила, действующая на него, —, угол между направлением силы и касательной к траектории элемента —.Положим (для определенности), что уголострый. При вращении тела каждый его элемент описывает окружность с центром на оси вращения. Для каждого элемента можно написать равенство вида (14):

,

где — угловое ускорение элемента с массой.

Просуммируем равенства по всем элементам :

.

Так как для абсолютно твердого тела угловое ускорение всех элементов одно и то же, то

Слева в равенстве стоит сумма моментов сил , действующих на все элементы тела. В теоретической механике доказывается теорема о том, что моменты суммы сил относительно какой-либо оси равен алгебраической сумме моментов этих сил относительно той же оси ( теорема Вариньона ).

Следовательно, слева в равенстве стоит величина вектора полного момента сил, действующих на тело, относительно той же оси вращения.

Величина равна сумме моментов инерции отдельных элементов относительно оси вращения и называется моментом инерциитела относительно оси.

Таким образом, основное уравнение вращательного движения теламожно записать в виде

.

Так как векторы всех моментов сил, действующих на элементы тела, откладываются на одной оси , то вектор полного момента сил также лежит на этой оси и связан с напрвлением результирующей силы правилом буравчика.