3.4.5 Парабола

Канонічне рівняння параболи

Параболою називається множина всіх точок площини, кожна з яких знаходиться на однаковій відстані від даної точки, що називається фокусом, і даної прямої, що називається директрисою. Відстань від фокуса F до директриси називається параметром параболи й позначається через р .

Виберемо систему координат так, щоб вісь проходила через фокус F перпендикулярно директрисі в напрямку від директриси до F, а початок координат О розташуємо всередині між фокусом і директрисою. В обраній системі координат фокус F має координати , а рівняння директриси має виглядабо.Канонічне рівняння параболи

. (3.16)

Доведення.

Нехай – довільна точка параболи. З'єднаємо точку М з точкою F. Проведемо відрізок MN перпендикулярно директрисі. За означенням параболи маємо . Оскільки ,, то. Звівши обидві частини рівняння у квадрат, одержимо,тобто .

Дослідження форми параболи

1. Парабола симетрична відносно осі , тому що в рівнянні (3.16) змінна у входить у парному ступені, тобто вісь є віссю симетрії параболи.

2. Парабола розташована праворуч від осі , тому що при видно, що .

3. Парабола проходить через початок координат, тому що при й.

Прийнято називати:

– точку вершиною параболи;

– відрізок FM=r фокальним радіусом точки М.

Парабола має вигляд, зображений на рис. 3.1.

Рисунок 3.1

Рівняння ,, також визначають параболи, вони зображені на рис.3.2, 3.3, 3.4.

Рисунок 3.2 Рисунок 3.3 Рисунок 3.4

Характеристики параболи

1. Прийнято називати директрисою параболи:

1) пряму;

2) пряму ;

3) пряму ;

4) пряму .

Директриса перпендикулярна осі симетрії параболи й розташована в тій напівплощині, де змінна, яка входить у рівняння параболи в першому ступені, не визначена.

2. Ексцентриситет параболи .

Рівняння параболи з осями симетрії, паралельними координатним осям

Нехай вершина параболи знаходиться в точці , осі симетрії паралельні координатним осямі.

Тоді рівняння параболи, зображеної на рисунку, має вигляд

.

Доведення.

Помістимо у вершині параболи початок нової системи координат . У цій системі координат рівняння параболи .

Оскільки , (див. формули паралельного переносу), то в старій системі координат рівняння параболи запишеться у вигляді

.

Параболи, зображені на рисунках 3.5, 3.6, 3.7, мають відповідно рівняння: ,,.

Рисунок 3.5 Рисунок 3.6 Рисунок 3.7

3.4.6 Загальне рівняння кривої другого порядку

Відомо, що загальне рівняння кривої другого порядку має вигляд:

,

де коефіцієнти ,іне дорівнюють нулю одночасно. Розглянемо два випадки: коефіцієнт; коефіцієнт.

У рівнянні загального вигляду коефіцієнт

Рівняння кола, еліпса, гіперболи, параболи з осями симетрії, паралельними координатним осям після найпростіших перетворень можна звести до загального рівняння кривої другого порядку (3.1), у якому коефіцієнт , тобто до рівняння виду

,

де коефіцієнти йне дорівнюють нулю одночасно. Має місце й зворотне твердження, що формулюється наступною теоремою.

Теорема. Рівняння означає:

1) при коло, уявне коло, точку;

2) при еліпс, уявний еліпс, точку;

3) при гіперболу, пару пересічних прямих;

4) при параболу, пару паралельних прямих.

Зауваження.

Надалі рівняння перерахованих кривих називатимемо канонічними. Рівняння, які визначають уявні криві, точку, прямі (пересічні або паралельні), називатимемо виродженими, а рівняння, які задають еліпс (коло), гіперболу, параболу – невиродженими.

Щоб перейти від рівняння до канонічного рівняння, здійснюють виділення повних квадратів за кожною змінною. У випадку невироджених кривих переходять до нової системи координат за допомогою паралельного переносустарих осей координат, депочаток нової системи координат щодо старої системи координат.

Доведення.

Проведемо для 1-го випадку.

Пряма задача. Рівняння кола (3.12) після розкриття дужок прийме вигляд

При порівнянні цього рівняння із загальним рівнянням (3.11) кривої другого порядку одержимо умови, за якими рівняння (3.11) переходить у рівняння кола: (коефіцієнти при й рівні між собою) і (відсутній член, що містить добуток поточних координат).

Зворотна задача. Загальне рівняння (3.11) за умови ,, тобто рівняннязвести до канонічного рівняння кола. Для цього виділяються повні квадрати за кожною змінною.

Перетворимо рівняння :

(3.13)

Звідки видно, що:

1. якщо ,то рівняння (3.13) визначає коло із центром у точці й радіусом ;

2. якщо ,то рівняння (3.13) набуде вигляду 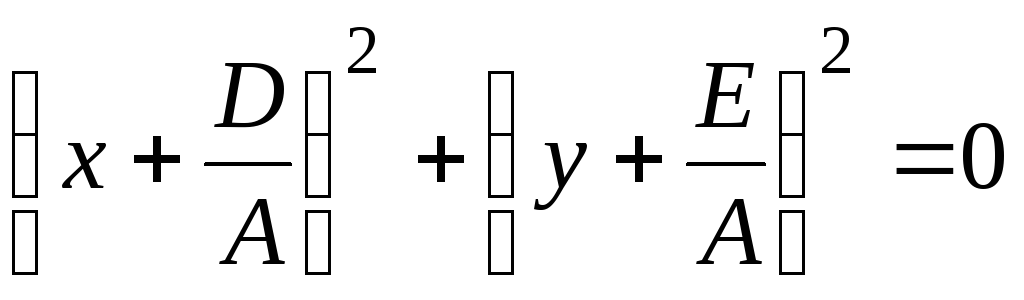і йому задовольняють координати єдиної точки (говорять: «коло виродилося в точку» або «має нульовий радіус»);

3. якщо , то рівняння (3.13) не визначає ніякої лінії, тому що права частина рівняння (3.13) від'ємна, а ліва частина– не від'ємна (говорять: «уявне коло»).

Теорему доведено.

Приклад.

Встановити тип кривої другого порядку та знайти всі її характеристики: для кола – координати центра та радіус; для еліпса – координати центра, півосі, координати фокусів, ексцентриситет, рівняння директрис; для гіперболи – координати центра, дійсну та уявну півосі, координати фокусів, ексцентриситет, рівняння директрис, рівняння асимптот; для параболи – параметр параболи, координати вершини, координати фокуса, рівняння директриси.

1. .

2. .

Розв'язання.

1. Оскільки , то рівняння визначає лінію еліптичного типу. Виділимо повні квадрати за кожною змінною:

; ;

; ;

.

Здійснивши паралельний перенос осей координат, прийнявши за новий початок точку , і скориставшись формулами перетворення координат,, одержимо в новій системі координат канонічне рівняння

,

яке визначає еліпс (рис. 3.8).Тоді точка - центр еліпса в системі координат, а точка- в системі координат. Півосі еліпса. Враховуючи, що, маємо. Звідки– фокуси еліпса в системі координат. Використовуючи співвідношення, отримаємо, що ексцентриситетта директрисив системі координат(тав системі координат).

Рисунок 3.8

2. Оскільки , то рівняння визначає лінію гіперболічного типу. Виділимо повні квадрати за кожною змінною:

; ;

; ;

; .

Останнє рівняння визначає дві пересічні прямі й.

У рівнянні загального вигляду коефіцієнт

Перетворимо загальне рівняння таким чином, щоб у ньому член з добутком координат був відсутній. Для цього здійснимо поворот координатних осей на кутза формулою .Або кут вибираємо так, щоЗвідки, знаючи ,можна знайти йза формулами,і подальше спрощення досягається за допомогою повороту координатних осей:

Доведення.

Використовуємо формули повороту осей

і виразимо старі координати через нові. Одержимо

.

Виберемо кут так, щоб коефіцієнт придорівнював нулю, тобто щоб виконувалася рівність

.

Тоді , тобто. Звідси .

З рівності одержимо, а розділивши на, маємо .

Зауваження.

1. Якщо , то в цьому випадку. Тоді , тобтой систему координат слід повернути на 45°.

2. Якщо вмовитися вважати кут повороту гострим, то у формулахбереться знак плюс.

Приклад.

Навести рівняння до канонічного вигляду. З'ясувати вид лінії другого порядку й зробити рисунок.

Розв'язання.

У даному рівнянні . Зробимо поворот координатних осей на кут, який знайдемо з рівняння.

Одержимо .

Знайдемо корінь рівняння: . Вибравши гострий кут, маємо,і

Підставляємо значення йу вихідне рівняння:

Розкриємо дужки й приведемо подібні члени. Після перетворень одержимо: , тобто маємо рівняння параболи з осями симетрії паралельними координатним осямі. Здійснивши паралельний перенос осей координат, прийнявши за новий початок точку , і скориставшись формулами перетворення координат,, одержимо в новій системі координат канонічне рівняння параболи: .

Для побудови параболи відзначимо на рисунку 3.9 повернені осі й. Для цього на осівідкладемо дві одиниці (в обраному масштабі), а на осі– одну. Одержимо точку, радіус-вектор якої нахилений до осіпід кутом. Через цю точкупроходить нова вісь. Далі в системі координатвідзначимо точку , що і буде початком нової системи координат . У системі координатбудуємо параболу, канонічне рівняння якої .

Рисунок 3.9

Контрольні запитання

1. Що називається лінією (кривою) другого порядку?

2. Що називається колом? Як задається канонічне рівняння кола із центром у точці й радіусом рівним?

3. Як задається рівняння кола з осями симетрії, які паралельні координатним осям?

4. Що називається еліпсом? Як задається канонічне рівняння еліпса?

5. Що називається фокальним радіусом, ексцентриситетом, директрисою еліпса?

6. Як задається рівняння еліпса з осями симетрії, паралельними координатним осям?

7. Що називається гіперболою? Як задається канонічне рівняння гіперболи?

8. Що називається фокальним радіусом, ексцентриситетом, директрисою гіперболи?

9. Якими рівняннями задаються асимптоти гіперболи?

10. Що називається параболою? Як задається канонічне рівняння параболи?

11. Як задається рівняння параболи з осями симетрії, паралельними координатним осям?

12. За яких умов рівняння визначає або еліпс, або уявний еліпс, або точку?

13. На який кут слід здійснити поворот координатних осей, щоб коефіцієнт при дорівнював нулю в загальному рівнянні?

116