3.4.4 Гіпербола

Канонічне рівняння гіперболи

Гіперболою називається множина точок площини, модуль різниці відстаней від кожної з яких до двох даних точок цієї площини, що називаються фокусами, є величина постійна, менша, ніж відстань між фокусами.

Позначимо фокуси через і, відстань між ними через 2с, а модуль різниці відстаней від кожної точки гіперболи до фокусів через 2а. За визначенням 2а<2с, тобто .

Д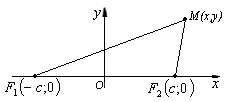ля одержання рівняння еліпса виберемо систему координатОху так, щоб фокуси йлежали на осіОх, а початок координат збігався з серединою відрізка . Тоді й– координати фокусів. Якщо ввести позначення , то одержимоканонічне рівняння гіперболи

. (3.15)

Доведення.

Нехай – довільна точка гіперболи. Тоді з визначення гіперболи одержимо, тобто

Позбудемося від ірраціональності:

Оскільки , то . Використовуючи позначення , останнє рівняння набуде виглядуабо

Дослідження форми гіперболи за її рівнянням

1. Рівняння (3.15) містить змінні х і у тільки в парних ступенях, тому й– осі симетрії, а точка – центр симетрії.

2. ,– точки перетину гіперболи з віссю , які визначаються, якщо покласти.

Прийнято називати:

– точки , вершинами гіперболи;

– відрізки й, а також їхньої довжини 2а й 2b дійсною й уявною осями гіперболи відповідно;

– числа а й b дійсною й уявною півосями гіперболи відповідно;

– , – фокальними радіусами точки М;

– –дійсною віссю,

– –уявною віссю.

3. З рівняння (3.15) необхідно, щоб або |x| а. Це означає, що точки гіперболи розташовані праворуч від прямої (права вітка гіперболи) і ліворуч від прямої (ліва вітка гіперболи).

Гіпербола має форму, зображену на рисунку (крива, що складається із двох необмежених віток).

Крива, обумовлена рівнянням , також є гіпербола, дійсна вісь 2b якої розташована на осі Оу, а уявна вісь 2а – на осі Ох. Гіпербола, у якої називається рівносторонньою. Її канонічне рівняння

Характеристики гіперболи

1. Величина – відношення половини відстані між фокусами до дійсної півосі гіперболи – називається ексцентриситетом гіперболи.

Оскільки с>а, то . Ексцентриситет характеризує форму гіперболи. Дійсно, з рівностівидно, щотобтойЗвідси чим менше ексцентриситет гіперболи, тим меншевідношення її півосей, а отже, вітки гіперболи притискаються до дійсної осі.

Для правої вітки гіперболи: і .

Для лівої вітки гіперболи: і .

2. Прямі х =±, які перпендикулярні дійсній осі, називаютьсядиректрисами гіперболи.

Оскільки для гіперболи , то .Таким чином, директриса х=розташована між центром і вершиноюгіперболи, а директрисах=– між центром і вершиною .

Зв'язок між ексцентриситетом і директрисою гіперболи: .

3. Прямі є асимптотами гіперболи.

Доведення.

Пряма L називається асимптотою необмеженої кривої К, якщо відстань d від точки М кривої К до цієї прямої прагне до нуля при необмеженому видаленні точки М уздовж кривої К.

Покажемо, що гіперболамає дві асимптоти. З огляду на симетрію гіперболий прямих , розглянемо тільки ті точки зазначених ліній, які розташовані в першій чверті.

Візьмемо на прямій точку N, яка має ту ж абсцису х, що й точка на гіперболій покажемо за допомогою означення асимптоти, що різницяMN між ординатами прямої і вітки гіперболи прагне до нуля при необмеженому видаленні точки М уздовж гіперболи. Дійсно

При знаменник збільшується, а дріб зменшується. Таким чином,, а, отже, і відстаньd прагне до нуля. Отже, прямі є асимптотами гіперболи.

Таким чином,при побудові гіперболи доцільно спочатку побудувати основний прямокутник гіперболи, провести прямі, що проходять через протилежні вершини цього прямокутника (асимптоти гіперболи), й вершини й гіперболи.

Очевидно, що гіперболи ймають загальні асимптоти. Такі гіперболи називаютьсясполученими.

Рівняння гіперболи з осями симетрії, паралельними координатним осям

Нехай центр гіперболи знаходиться в точці , осі симетрії паралельні координатним осямі, дійсна й уявна півосі рівні відповідноа й b.

Тоді рівняння гіперболи має вигляд

Доведення.

Помістимо в центрі гіперболи початок нової системи координат . У цій системі координат рівняння гіперболи

.

Оскільки , (див. формули паралельного переносу), то в старій системі координат рівняння гіперболи запишеться у вигляді