2. Спіраль Архімеда.

Названа на честь давньогрецького вченого Архімеда (біля 287-212 до н.е.).

Полярне рівняння .

Якщо – стала, то. Якщо, то. Точка, яка належить спіралі Архімеда, рухається навколо полюса, одночасно віддаляючись від нього.

3. Лемніската Бернуллі.

Назву дав швейцарський математик Я. Бернуллі (1654–1705).

Полярне рівняння (– неявне рівняння). Ця лемніската наведена на рисунку.

Лемніската, рівняння якої , повернута відноснона 45⁰.

4. Завиток Паскаля.

Названий на честь батька французького математика-аматора (1588-1651) Ет'єна Паскаля.

Полярне рівняння – неявне рівняння

_{5. Кардіоїда.}

Призавиток Паскаля перетворюються в кардіоїду, рівняння якої

6. Трипелюсткова троянда.

Полярне рівнянняОскільки, що, то.

Звідки

_{а тому кут, який відповідає одній пелюстці, дорівнює .}

Рівняння й рисунки деяких кривих, заданих параметричними рівняннями

1. Астроїда.

З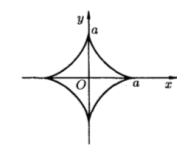адається рівняннями

( в неявному вигляді ).

2. Циклоїда.

Задається рівняннями

.

Параметр визначає кут повороту радіуса кола, що проходить через фіксовану точку. Циклоїда – це крива, яку описує фіксована точка окружності, що котиться без ковзання по осі Ох.

3. Напівкубічна парабола.

Крива названа на честь англійського математика У.Нейля (1637-1670).

Задається рівняннями .

(Рівняння в неявному вигляді .)

Контрольні запитання

1. Що називається рівнянням лінії на площині?

2. Яким рівнянням визначається лінія в полярній системі координат? Навести приклади.

3. Як записуються параметричні рівняння лінії? Навести приклади.

4. Як записується векторне рівняння лінії?

3.3 Пряма лінія

Існують різні способи завдання прямої лінії на площині в декартовій системі координат. Наведемо основні види рівнянь прямої.

Рівняння прямої з кутовим коефіцієнтом

Положення довільної прямої на площиніцілком визначається ординатоюb точки перетину з віссю й кутом між віссю Ох і прямою, де кут () – це найменший кут між позитивним напрямком осіта даною прямою.

Візьмемо на прямій довільну точку . Опустимо з неї на вісь перпендикуляр. Проведемо через точку N пряму, що паралельна осі , до перетину з перпендикуляром. У побудованому трикутнику, тобто. Введемо позначення , одержуємо рівняння

, (3.4)

якому відповідають координати будь-якої точки прямої.

Число називається кутовим коефіцієнтом прямої, а рівняння (3.4) – рівнянням прямої з кутовим коефіцієнтом.

Окремі випадки:

1) – рівняння прямої, що проходить через початок координат;

2) – рівняння прямої, що паралельна осі;

3) – рівняння прямої, що паралельна осі, деа – абсциса точки перетину прямої з віссю . (Якщо пряма паралельна осі, тойрівняння (3.4) втрачає зміст, бо для неї кутовий коефіцієнтне існує.)

Нехай пряма, задана рівнянням , проходить через точку, тобто координати точки задовольняють рівняння прямої:. Звідси .Підставляючи значення b у рівняння , одержимо шукане рівняння прямої , тобто

,

яке називається рівнянням прямої, що проходить через точку, із заданим кутовим коефіцієнтом.

Рівняння прямої у векторно-параметричному, параметричному й канонічному вигляді

Положення довільної прямої на площинівизначається точкою, що належить прямій, і векторомпаралельним даній прямій, який називаєтьсянапрямним вектором прямої. Нехай – довільна точка на прямій. Позначимо черезїї радіус-вектор, через– радіус-вектор точки. Оскільки векторє колінеарним вектору, то, використовуючи необхідну й достатню умову колінеарності двох векторів, одержимо рівняння

, (3.5)

яке називається векторно-параметричним, де – параметр.

Запишемо рівняння (3.5) через координати. Одержимо рівняння

(3.6)

які називаються рівняннями прямої в параметричному вигляді.

Виключивши параметр із рівнянь (3.6), одержимо так зване канонічне рівняння прямої:

. (3.7)

Рівняння прямої, що проходить через дві точки

Нехай пряма проходить через точки й. Тоді за напрямний вектор прямої можна взяти векторі в рівнянні (3.7) замістьіпідставити відповідно й .Одержимо рівняння прямої, що проходить через точки й:

(3.8)

Передбачається, що в цьому рівнянні .

Окремі випадки:

1) – пряма, що проходить через точкий, паралельна осі ординат і її рівняння;

2) – прямапаралельна осі абсцис і її рівняння.

Рівняння прямої у відрізках

Н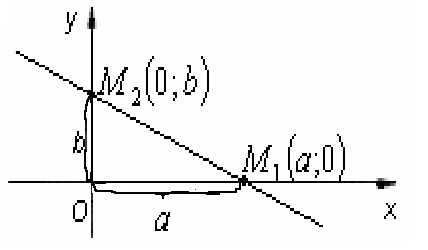ехай пряма перетинає вісьОх у точці , а вісьОу – у точці . У цьому випадку рівняння (3.8) прийме вигляд тобто

.

Це рівняння називається рівнянням прямої у відрізках, тому що числа а й b указують, які відрізки відтинає пряма на осях координат.

Рівняння прямої, що проходить через точку перпендикулярно вектору

Знайдемо рівняння прямої, що проходить через задану точку перпендикулярно даному ненульовому вектору . Візьмемо на прямій довільну точкуй розглянемо вектор. Тому що вектори йперпендикулярні, то й їхній скалярний добуток дорівнює нулю:, тобто

. (3.9)

Це рівняння називається рівнянням прямої, що проходить через задану точку перпендикулярно заданому вектору.

Вектор , перпендикулярний прямій, називається нормальним вектором цієї прямої.

Рівняння прямої в загальному вигляді

У рівнянні (3.9) розкроїмо дужки, введемо позначення . Тоді воно прийме вигляд

.

де А і В – координати нормального вектора . Отримане рівняння називається рівнянням прямої взагальному вигляді.

Окремі випадки:

1) якщо , то ||;

2) якщо , то ||;

3) якщо , то проходить через початок координат;

4) якщо , то збігається з;

5) якщо , то збігається з.

Нормальне рівняння прямої

Розглянемо прямокутну систему координат Оху. Позначимо через відстань від початку координатО до прямої .

Якщо:

1), де;

2)||, дей;

3)– радіус-вектор точки , то. З огляду на те, що, одержимо

. (3.10)

Рівняння (3.10) називається нормальним рівнянням прямої.

Покажемо, як навести рівняння прямої в загальному вигляді до нормального рівняння (3.10). Помножимо рівняння прямої в загальному вигляді на деякий множник . Одержимо

.

Через те, що остання рівність має дорівнювати (3.10), то одержимо ,, . Використовуючи властивість напрямних косинусів: , маємо , звідки множник, що нормує . Відповідно до рівності , знак множника, що нормує, протилежний знаку вільного члена загального рівняння прямої.

Відстань від точки до прямої

Н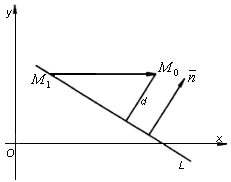ехай задані прямарівнянням і точка .

Відстань d від точки до прямоїL дорівнює модулю проекції вектора , де – довільна точка прямої L, на напрямок нормального вектора . Отже,

Оскільки точка належить прямій L, то , тобто . Тому

.

Якщо пряма задана нормальним рівнянням , то з огляду на те, що , , , де , тобто , , , одержимо

.

Кут між прямими

1.Нехай прямі йзадані рівняннями з кутовими коефіцієнтамийЗнайдемо найменший із двох суміжних кутів, які вони утворять.

Маємо (теорема про зовнішній кут трикутника) або . Якщо , то

.

Але , тому

Окремі випадки:

1) – умова ||;

2) – умова.

2. Нехай прямі йзадані канонічними рівняннями.

: , дей– напрямний вектор;

: , дей– напрямний вектор.Один з двох кутів між прямими ідорівнює кутуміж напрямними векторамита, а інший. Томутреба брати за модулем, тобто

_.

Окремі випадки:

1) – умова ||;

2) – умова .

3. Нехай прямі ізадані рівняннями в загальному вигляді.

: , де – нормальний векторі;

: , де – нормальний векторі.

Тоді і відповідно один з гострих кутів визначається за формулою

_.

Окремі випадки:

1) – умова ||;

2) – умова .

Приклад.

Задані прямі ,і точка, де:і,;:і;.

Знайти:

1. канонічне, з кутовим коефіцієнтом і в загальному вигляді рівняння прямої ;

2. рівняння прямої в загальному вигляді;

3. параметричні рівняння прямої ;

4. рівняння прямої у відрізках;

5. рівняння прямої , що проходить через точкупаралельно прямій;

6. рівняння прямої , що проходить через точкуперпендикулярно прямій;

7. відстань від точки до прямої;

8. кут між прямими і.

Розв'язання.

1. Оскільки пряма проходить через дві точкий, то за формулоюодержимоабо– канонічне рівняння (3.7) прямої. З останнього рівняння– рівняння з кутовим коефіцієнтом вигляду, де,. Записавши рівняння з кутовим коефіцієнтом у вигляді неявної функції, одержимо рівняння прямоїв загальному вигляді.

2. Скористаємося рівнянням прямої (3.9), що проходить через точку перпендикулярно вектору, яке у нових позначеннях має вигляд: . Одержимоабо– рівняння прямоїв загальному вигляді.

3. Щоб одержати параметричні рівняння (3.6) прямої , дорівняємо канонічне рівняння прямої до параметра:. Звідси

4. Рівняння прямої у відрізках має вигляд , де й з точністю до знака визначають довжини відрізків, що відтинаються прямою на відповідних осях координат Ох і Оу. Рівняння прямої з пункту 2 має вигляд . Звідси одержимоабо, де,.

5. З п.1:. Оскільки||, то||, де,– нормальні вектори прямихі. З огляду на те, що, за формулою (3.9), що визначає пряму, що проходить через точку перпендикулярно вектору, одержимо рівняння: або в загальному вигляді .

6. З п.2Запишемо рівняння прямоїв канонічному виглядіде||ОтримаємоабоТоді , де. Через те, щоі, де– нормальний вектор прямої, то за формулою (3.9), маємо, або :.

7. Відстань від точки до прямої: обчислюється за формулою . Оскільки:,, то.

8. Кут між прямими : і : ,визначається за формулою _{Звідси .}

Контрольні запитання та завдання

1. Вивести рівняння прямої з кутовим коефіцієнтом.

2. За якою формулою записується рівняння прямої з кутовим коефіцієнтом, що проходить через задану точку?

3. Що називається напрямним вектором прямої?

4. За якою формулою записується рівняння прямої , що проходить через задану точку паралельно заданому вектору?

5. Вивести параметричні рівняння прямої на площині.

6. За якою формулою записується рівняння прямої, що проходить через дві задані точки?

7. Вивести рівняння прямої у відрізках.

8. За якою формулою записується рівняння прямої , що проходить через задану точку перпендикулярно заданому вектору?

9. Що називається нормальним вектором прямої?

10. Яке рівняння прямої називається рівнянням у загальному вигляді? Навести окремі випадки.

11. Вивести нормальне рівняння прямої.

12. Як визначається відстань від точки до прямої на площині?

13. За якими формулами визначається кут між прямими?