3 Аналітична геометрія на площині

3.1 Система координат на площині

Раніше була введена декартова система координат у просторі (див. п.2.3), де кожній точці простору відповідає трійка чисел. Підсистемою координат на площині розуміють спосіб, що дозволяє чисельно описати положення точки площини. Розглянемо різні способи завдання системи координат на площині.

Прямокутна (декартова) система координат

Прямокутна система координат задається двома взаємноперпендикулярними прямими – осями, на кожній з яких обраний позитивний напрямок і заданий одиничний відрізок. Ці осі називають осями координат. Точку їхнього перетинання О – початком координат. Одну з осей називають віссю абсцис або віссю , іншу – віссю ординат або віссю .

Одиничні вектори осей позначають і (, ) .

Систему координат позначають , а площина, у якій розташована система координат, називають координатною площиною.

Вектор довільної точкиназиваєтьсярадіус-вектором точки .

Координати точки у системі координат дорівнюють координатам радіус-вектора й позначають:;, де число називається абсцисою точки , – ординатою точки .

Числа й повністю визначають положення точки на площині, а саме: кожній парі чисел і відповідає єдина точка М площини, і навпаки.

Полярна система координат

Полярна система координат задається точкою О, яка називається полюсом, і променем (), який називається полярною віссю, а положення точки – двійкою чисел , які називаютьсяполярними координатами точки , де числа– відстань від полюсаО до точки і– кут, на який треба повернути полярну вісьОА до її збігу з ОМ, проти годинникової стрілки. При цьому називають полярним радіусом, – полярним кутом.

Полярний радіусможе змінюватися у межах, полярний кут, як правило, змінюється в межахабо.

У цьому випадку кожній точці площини (крім О) відповідає єдина пара чисел і , і навпаки.

В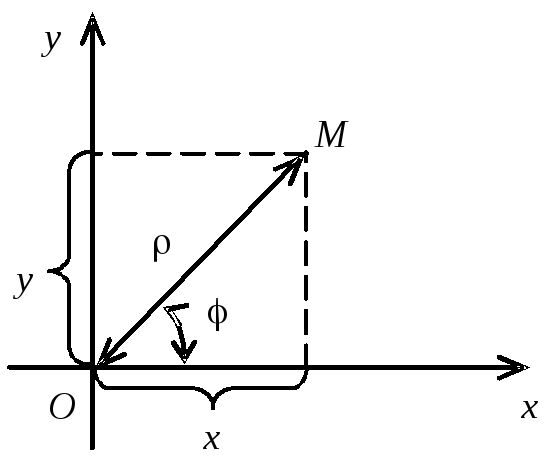становимо зв'язок між прямокутними й полярними координатами. Для цього сполучимо полюсО з початком координат системи , а полярну вісь – з додатною піввіссю Ох. Нехай і – прямокутні координати точки , а й – її полярні координати.

Прямокутні координати точки виражаються через полярні координати точки за формулами:

Полярні ж координати точки виражаються через її декартові координати такими формулами:

Визначаючи величину , слід встановити (по знаках і ) чверть, у якій лежить шуканий кут. Якщо полярний кут змінюється в межах, то зручніше користуватися такими формулами:

(3.2)

Приклад.

Дана точка . Знайти її полярні координати.

Розв'язання.

Обчислимо полярний радіуста за формулою (3.2) полярний кут . Таким чином, полярні координати точки .

Перетворення системи координат

Перехід від однієї системи координат в будь-яку іншу називається перетворенням системи координат.

Розглянемо два випадки перетворення однієї прямокутної системи координат в іншу: паралельний перенос та поворот осей координат.

1. Паралельний перенос осей координат

Нехай на площині задана прямокутна система координат. Підпаралельним переносом осей координат від системи координат до нової системи розуміють перехід, при якому міняється положення початку координат, а напрямок осей і масштаб залишаються незмінними.

Нехай у старій системі координат початок нової системи координат точкамає координати, тобто . Позначимо координати довільної точки М площини в старій системі координат через , а в новій системі через. Розглянемо вектори в старій і новій системах координат:

, ,.

Оскільки , то , тобто . Отже,

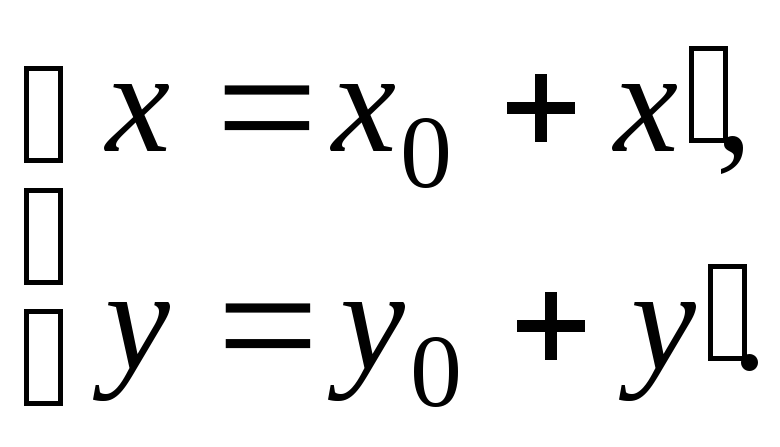
Отримані формули дозволяють знаходити старі координати x і у за відомими новими і , і навпаки.