Розв’язок.

Функція 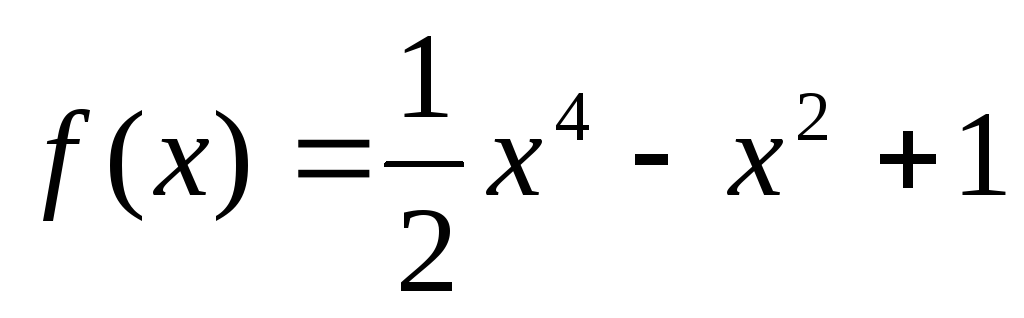неперервна на відрізку [-1, 1] як елементарна. Її похідна дорівнює . Дорівнюємо похідну до 0 для знаходження критичних точок; маємо . Розв’язуємо рівняння та отримуємо точки: х = -1, х = 0, х = 1. Всі точки належать до відрізку [-1, 1].

Знаходимо значення функції в кожній критичній точці. Маємо: ƒ(-1) = ½, ƒ(0) = 1, ƒ(1) = ½. Тому, найбільше значення функція має в точці х = 0, найменше – в точках х = -1, х = 1.

4. Нехай потрібно знайти найбільше чи найменше значення геометричної чи фізичної величини, що задовольняє деякі умови. Тоді потрібно представити цю величину як функцію деякого аргументу. З умови задачі визначається проміжок змінення цього аргументу. Далі використовується схема дослідження функції на найбільше чи найменше значення функції на проміжку.

Приклади: 2) Задача. Відрізок АВ = а розділяється на дві частини точкою

С; на відрізках АС та СВ, як на сторонах, будується прямокутник АВСD. Визначити найбільше значення його площі S.

Розв’язок.

Нехай аргументом х є довжина відрізку АС, тоді СВ = а – х, S = х(а - х). Аргумент х неперервної функції S змінюється в проміжку [0, а]. Досліджуємо функцію S на найбільше значення на відрізку [0, а]. Маємо: S′(х) = а - 2х, а – 2х = 0, х = а/2. Знайдена критична точка належить до відрізку [0, а]. Значення функції в точках х = а, х = а/2, х = 0 такі: S(а) = 0, S(а/2) = а²/4, S(0) = 0. Тому найбільшим значенням площі прямокутнику є S(а/2) = а²/4, тобто квадрат із стороною а/2 має найбільшу площу серед всіх прямокутників заданої площі.