
ман для 1ПМ-11 / МАН - ТЕСТЫ / тесты 2, 3, 4 курсы / ман - тест часть 11
.docТести до державного іспиту.
Математичний аналіз. Частина 11.
-
Дана множина точок, у яких перша координата раціональна, а друга – ірраціональна. Що є межею цієї множини?
а) вся площина; •
б) множина точок, у якої перша координата ірраціональна, а друга раціональна;
в)множина точок, у якої обидві координати раціональні;
г)не можливо встановити;
-
Яка з функцій має лінію точок розриву?
а)
![]() ;
;
б)
![]() ;
•
;
•
в)
![]() ;
;
г)
![]() ;
;
-
Для функції
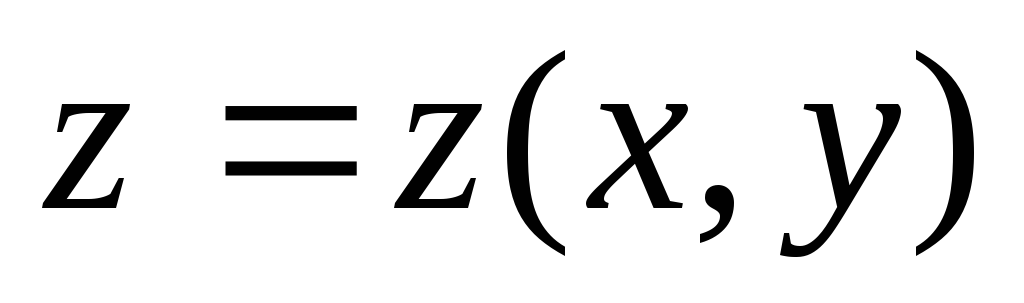 точка
точка
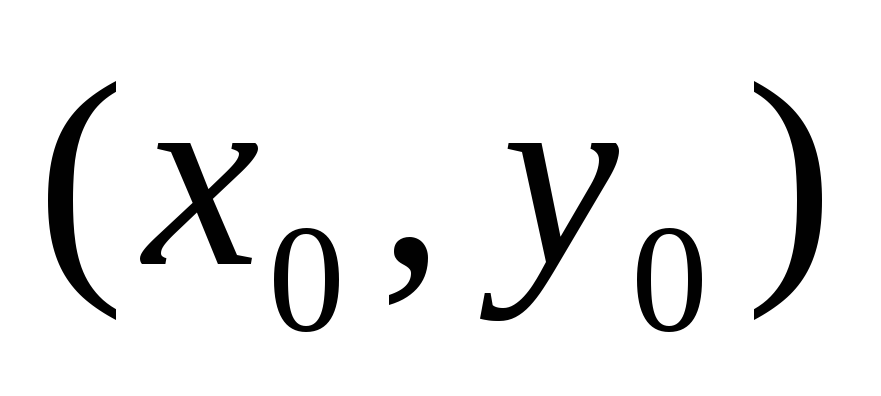 - стаціонарна. Яка з умов достатня для
того, щоб у цій точці не було екстремуму?
- стаціонарна. Яка з умов достатня для
того, щоб у цій точці не було екстремуму?
а)
![]() ;
;
б)
![]() ;
•
;
•
в)
![]() ;
;
г)
![]() ;
;
-
Нехай
 .
Тоді
.
Тоді
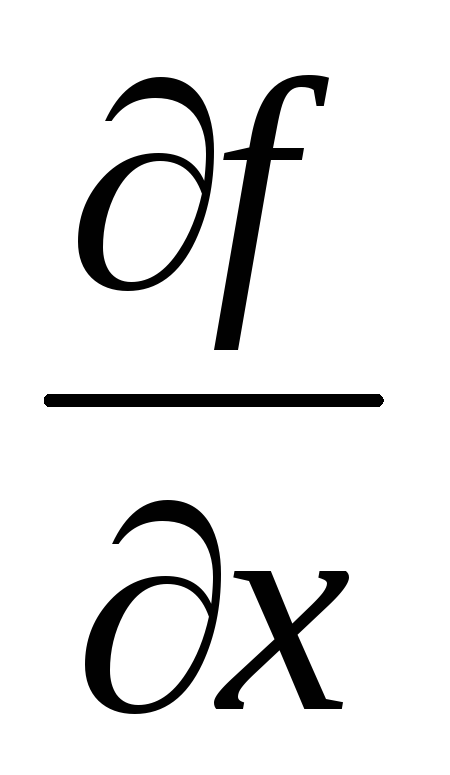 дорівнює:
дорівнює:
а)
![]() ;
•
;
•
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
-
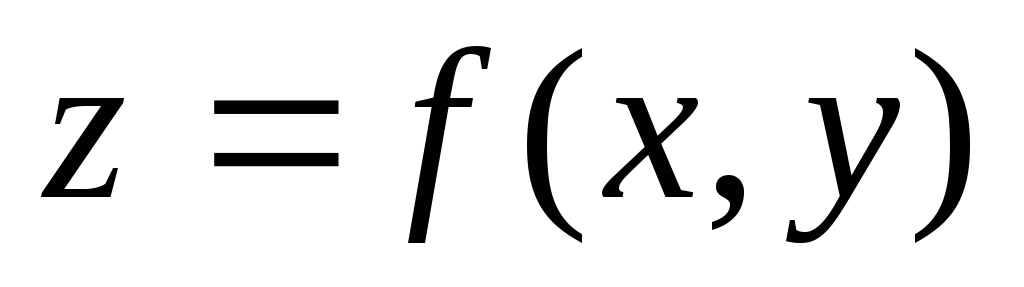 диференційована
в точці
диференційована
в точці
 .
Який варіант відповіді невірний?
.
Який варіант відповіді невірний?
а)
![]() ;
•
;
•
б) існують
![]() та
та
![]() у точці
у точці
![]() ;
;
в)
![]() ;
;
г)
![]() неперервна
в точці
неперервна
в точці
![]()
-
Яке з тверджень не гарантує диференційованість
 в точці
в точці
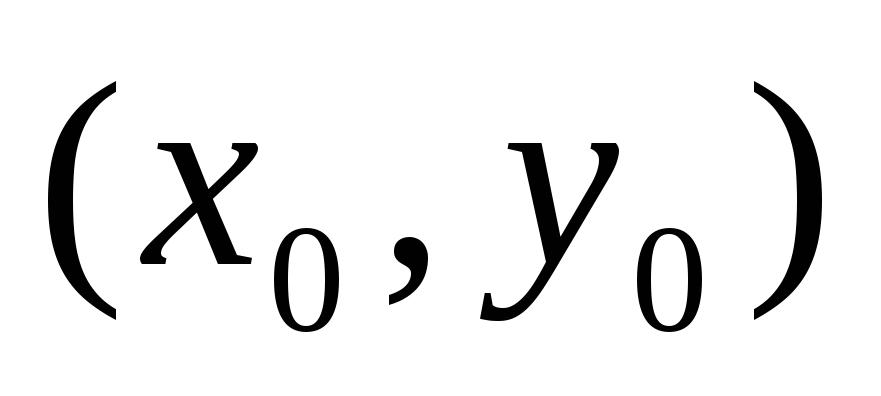 ?
?
а) існує
неперервний градієнт у точці
![]() ;
;
б) приріст
функції можна записати так:
![]()
в) існують
![]() та
та
![]() у точці
у точці
![]() ;
•
;
•
г) приріст
функції можна записати так:
![]()
-
Яке з тверджень не гарантує диференційованість
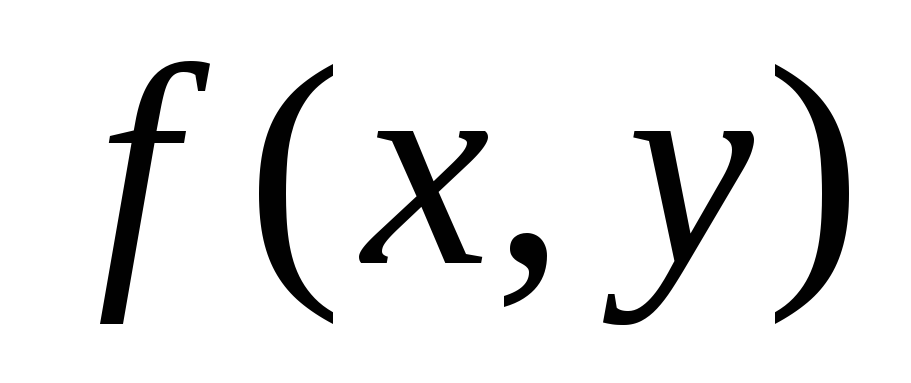 в точці
в точці
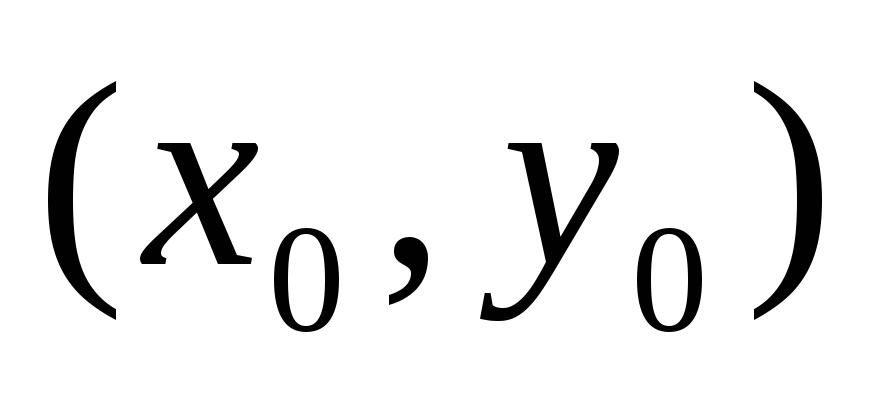 ?
?
а) існують
![]() та
та
![]() у точці
у точці
![]() ;
•
;
•
б) існує
неперервний градієнт у точці
![]() ;
;
в) приріст
функції можна записати так:
![]() ;
;
г) приріст
функції можна записати так:
![]() ;
;
-
Для функції
 точка
точка
 - стаціонарна. Яка з умов достатня для
того, щоб у цій точці не було екстремуму?
- стаціонарна. Яка з умов достатня для
того, щоб у цій точці не було екстремуму?
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
•
;
•
г)
![]() ;
;
-
Дотична площина до поверхні
 в точці (0, 0, 0) має рівняння:
в точці (0, 0, 0) має рівняння:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
•
;
•
г)
![]() ;
;
-
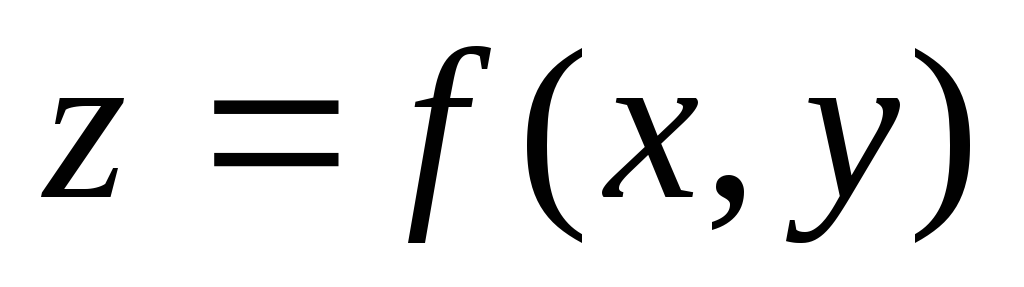 диференційована
в точці
диференційована
в точці
 .
Який варіант відповіді невірний?
.
Який варіант відповіді невірний?
а) існують
![]() та
та
![]() у точці
у точці
![]() ;
;
б)
![]() ;
;
в)
![]() неперервна
в точці
неперервна
в точці
![]()
г)
![]() ;
•
;
•
-
Чи може необмежена на множині
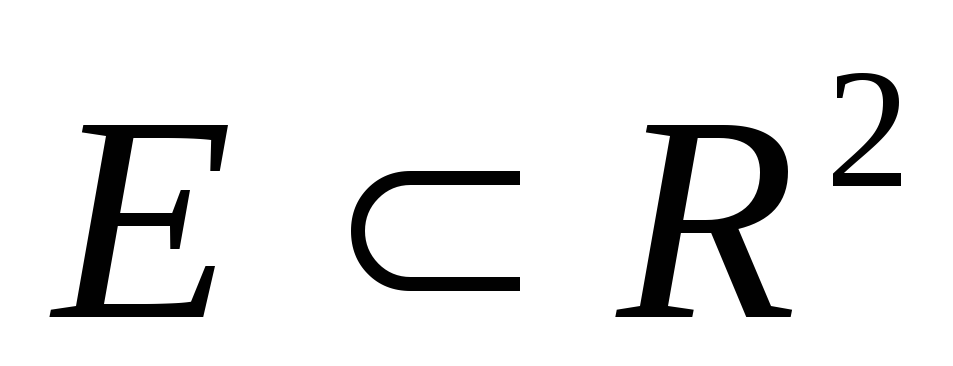 функція
функція
 бути неперервною на
бути неперервною на
 ,
якщо:
,
якщо:
а)
![]() ;
•
;
•
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
-
Функція
 необмежена і неперервна. На якій з
областей вона визначена?
необмежена і неперервна. На якій з
областей вона визначена?
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
•
;
•
г)
![]() ;
;
-
Дотична площина до поверхні
 в точці (0, 0, 0) має рівняння:
в точці (0, 0, 0) має рівняння:
а)
![]() ;
•
;
•
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
-
 - точка
локального максимуму для
- точка
локального максимуму для
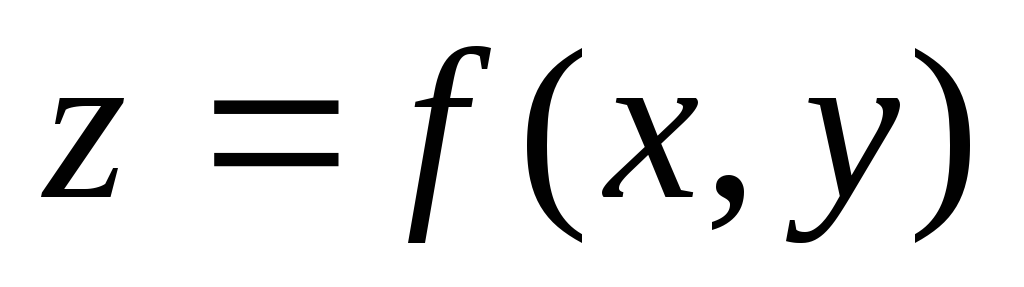 . Яке з тверджень вірне?
. Яке з тверджень вірне?
а)
![]() -
не диференційована у точці
-
не диференційована у точці
![]() ;
;
б)
![]() -
означена у точці
-
означена у точці
![]() ;
•
;
•
в)
![]() диференційована в точці
диференційована в точці
![]()
г)
![]() = 0,
= 0,
![]() = 0 у точці
= 0 у точці
![]() ;
;
-
Нехай
 .
Тоді
.
Тоді
 дорівнює:
дорівнює:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
•
;
•
-
Яка з плоских множин є і не відкритою і не замкненою?
а)
![]() ;
•
;
•
б)
![]() ;
;
в) жодна з плоских множин не відповідає цим умовам;
г)
![]() ;
;
-
Яка з функцій не має жодного локального екстремуму?
а)
![]() ;
;
б)
![]() ;
•
;
•
в)
![]() ;
;
г)
![]() ;
;
-
Яка з плоских множин є відкритою?
а) жодна з плоских множин не є відкритою;
б) x ≤y <x² +1;
в) y <x <2y; •
г) x ≤y ≤x² +1;
-
Яка з плоских множин є замкненою?
а) жодна з плоских множин не є замкненою;
б)
![]() ;
•
;
•
в)
![]() ;
;
г)
![]() ;
;
-
Нехай
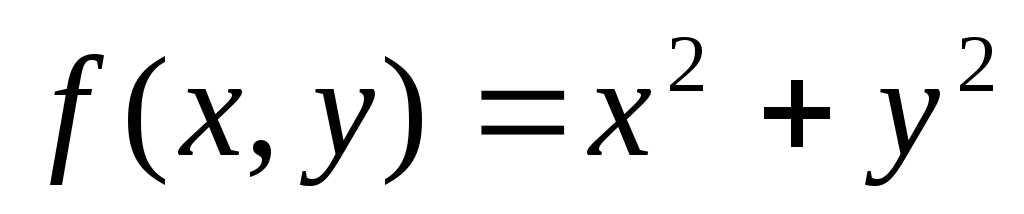 .
Тоді (0, 0) є точкою:
.
Тоді (0, 0) є точкою:
а) глобального максимуму;
б) розриву для цієї функції;
в) мінімуму; •
г) локального мінімуму;
-
Область визначення функції
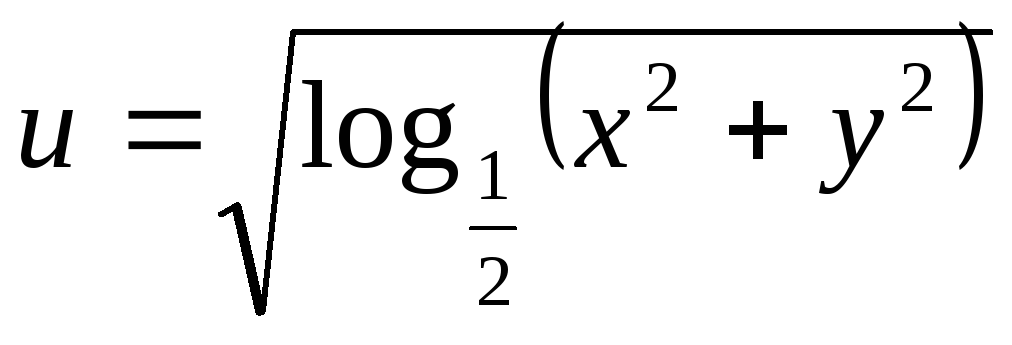 :
:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
•
;
•
г)
![]() ;
;
-
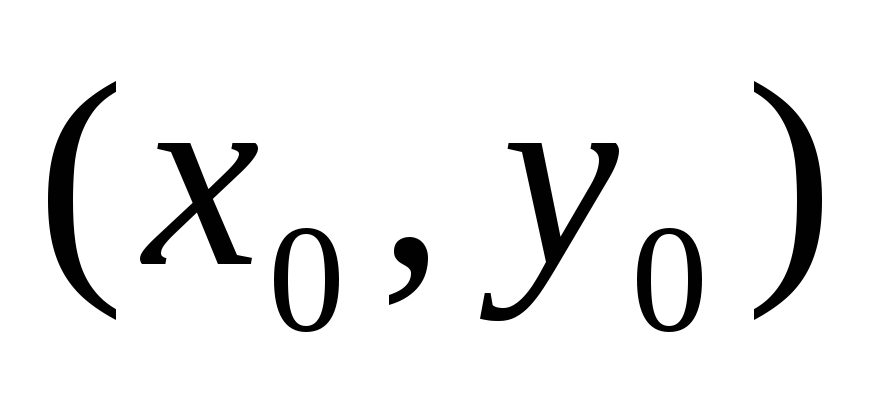 - точка
локального максимуму для
- точка
локального максимуму для
 . Яке з тверджень вірне?
. Яке з тверджень вірне?
а)
![]() -
диференційована у точці
-
диференційована у точці
![]() ;
;
б)
![]() -
означена у точці
-
означена у точці
![]() ;
•
;
•
в)
![]() = 0,
= 0,
![]() = 0 у точці
= 0 у точці
![]() ;
;
г)
![]() не диференційована в точці
не диференційована в точці
![]()
-
Яка з плоских множин є відкритою?
а)
![]() ;
•
;
•
б)
![]() ;
;
в)
![]() ;
;
г) жодна з плоских множин не є замкненою;
-
Чи може необмежена на множині
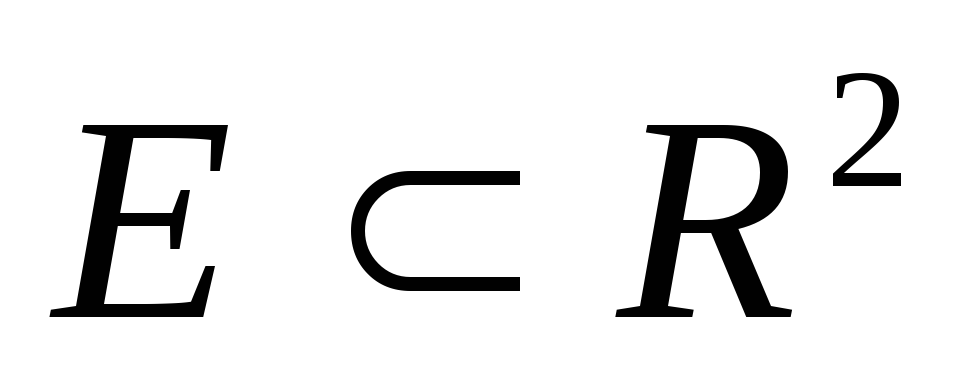 функція
функція
 бути неперервною на
бути неперервною на
 ,
якщо:
,
якщо:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
•
;
•
-
Нехай
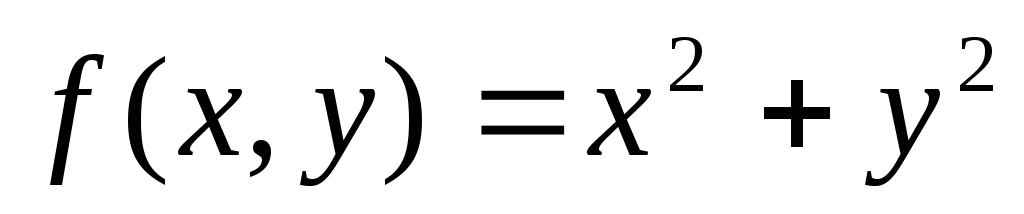 .
Тоді (0, 0) є точкою:
.
Тоді (0, 0) є точкою:
а) мінімуму; •
б) розриву для цієї функції;
в) глобального максимуму;
г) локального мінімуму;
-
Область визначення функції
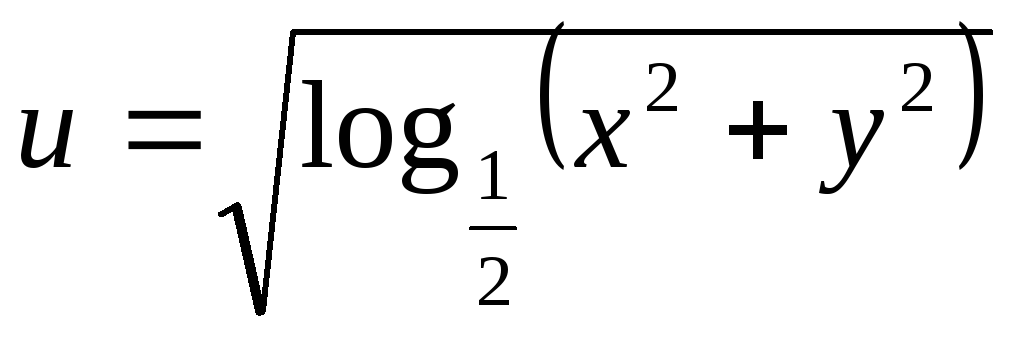 :
:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
•
;
•
-
Функція
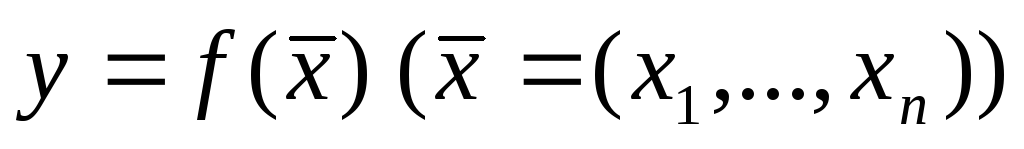 неперервна на множині
неперервна на множині
 .
Яке твердження правильне?
.
Яке твердження правильне?
а) графік
функції
![]() в
кожній точці
в
кожній точці
![]() має дотичну площину;
має дотичну площину;
б)
![]() ;
;
в)
![]() диференційована
у внутрішніх точках Е
диференційована
у внутрішніх точках Е
г)
![]() обмежена
на Е; •
обмежена
на Е; •
-
Дана множина точок у яких перша координата раціональна, друга - ірраціональна. Що є межею цієї множини?
а) множина точок, у якої перша координата ірраціональна, друга – раціональна;
б) не можливо встановити;
в) множина точок, у якої обидві координати раціональні;
г) вся площина; •
-
Яка з плоских множин є і не відкритою і не замкненою?
а) жодна з плоских множин не відповідає цим умовам;
б) y <x <2y;
в) x ≤y ≤x² +1;
г) x ≤y <x² +1; •
-
Яка з плоских множин є замкненою?
а)
![]() ;
;
б)
![]() ;
•
;
•
в) жодна з плоских множин не є замкненою;
г)
![]() ;
;
-
Яка з функцій має лінію точок розриву?
а)
![]() ;
;
б)
![]() ;
•
;
•
в)
![]() ;
;
г)
![]() ;
;
-
Яка з функцій не має жодного локального екстремуму?
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
•
;
•
-
Функція
 необмежена і неперервна. На якій з
областей вона визначена?
необмежена і неперервна. На якій з
областей вона визначена?
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
•
;
•
-
Функція
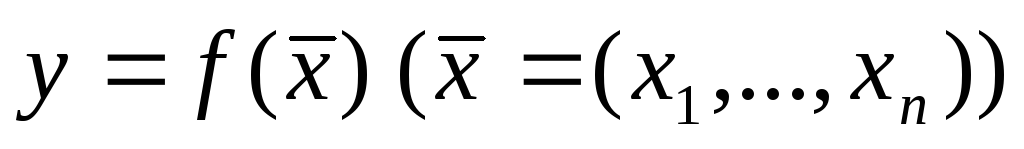 неперервна на компактній множині
неперервна на компактній множині
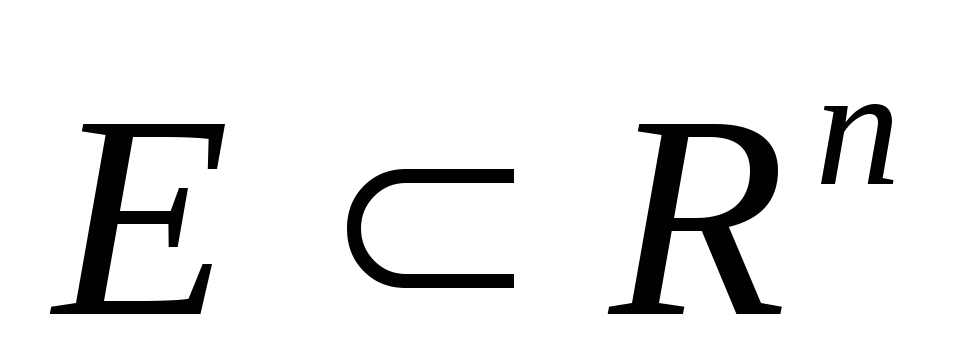 .
Яке твердження правильне?
.
Яке твердження правильне?
а)
![]() ;
;
б) графік
функції
![]() в
кожній точці
в
кожній точці
![]() має дотичну площину;
має дотичну площину;
в)
![]() диференційована
у внутрішніх точках Е
диференційована
у внутрішніх точках Е
г)
![]() обмежена
на Е; •
обмежена
на Е; •
