
ПРЗ-1_Уравнения и неравенства
.pdf
Ответ: 32.
Пример 5.18. Решите уравнение

 5х2 20х 21
5х2 20х 21 
 3х2 12х 28 8х 2х2 3.
3х2 12х 28 8х 2х2 3.
Решение. ОДЗ: х R .
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
5х2 20х 21 3х2 12х 28 5(x 2)2 1 3(x 2)2 16 1 16 5. |
|||||||||||||||||||
Равенство |
достигается |
при |
х = 2. |
С |
другой |
|
стороны, |
|||||||||||||
8х 2х2 3 2(х 2)2 5 5, причем равенство достигается |
при х = 2. |
|||||||||||||||||||
Значит, единственный корень уравнения х = 2. |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Ответ: 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Пример 5.19. Решите уравнение (х 8)(4 х)( |
|
|
|||||||||||||||||
|
х 8 2) 1. |
|||||||||||||||||||
|
Решение. ОДЗ: х 8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
При х 8. х 8 16 0; 4 x 4 0; |
x 8 2 2 0 . |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Значит, (х 8)(4 х)( |
х 8 2) 0 1. |
|
|
|
|
|
|
|
|
|
|
||||||||
|
Ответ: корней нет. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
ИДЕЯ СОПРЯЖЕННОСТИ В ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЯХ |
|
|||||||||
|
При |
решении |
иррациональных |
уравнений |
вида |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) |
g(x) h(x) , где |
(0; ), (0; ); |
f (x), g(x), h(x) — |
|||||||
рациональные функции, можно использовать такой алгоритм: |
|
||||||||||
|
|
|
|
|
|
|
|
||||
|
Рассмотрим уравнение |
|
f (x) g(x) h(x). |
|
|||||||
1. Составим из данного исходного уравнения новое, в левой части которого выражение, сопряженное с выражением, стоящим в левой части исходного уравнения, а в правой содержится новая неизвестная функция
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) g(x) h(x) |
|
||||||||||
|
|
|
|
|
|
|
|
||||||||||
t(x). Составим систему: |
|
|
|
|
|
|
|
|
|
|
. |
||||||
|
|
|
|
|
|
|
f (x) |
|
g(x) t(x) |
|
|||||||
2. Перемножим исходное уравнение с новым и получим выражение |
|||||||||||||||||
t(x) через х. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||||||
( f (x) g(x))( |
f (x) g(x) h(x) t(x) 2 f (x) 2 g(x) h(x) t(x) . |
||||||||||||||||
Решая полученное уравнение относительно х, получим некоторые корни, которые проверяются непосредственно подстановкой в исходное
уравнение и выражение для функции t(x). |
|
|
|||||
|
3. Сложим |
исходное |
и |
новое |
уравнения, |
получим: |
|
|
|
|
|
|
|
||
2 |
f (x) h(x) t(x) или 2 |
g(x) h(x) t(x) , |
из которого найдем все |
||||
другие корни. Снова обязательно проверим все корни.
Пример 5.20. Решите уравнение: 
 х3 х2 1
х3 х2 1 
 х3 х2 2 3 .
х3 х2 2 3 .
Решение. Составим уравнение 
 х3 х2 1
х3 х2 1 
 х3 х2 2 А. Умножив на исходное уравнение, получим
х3 х2 2 А. Умножив на исходное уравнение, получим
(х3 х2 1) (х3 х2 2) 3А .
51

х3 х2 1 х3 х2 2 3А ; 3А 3; А= –1.
|
|
|
|
|
|
|
|
|
||||
Тогда |
х3 х2 1 |
|
х3 х2 2 1. Сложив исходное уравнение и |
|||||||||
|
|
|
|
|
|
|
|
|
||||
полученное, |
имеем |
2 |
х3 х2 1 2; |
|
х3 х2 1 1; |
х3 х2 |
1 1; |
|||||
х3 х2 2 0 , |
откуда |
х = 1. Проверка |
показывает, что |
х = 1 — |
корень |
|||||||
уравнения.
Ответ: 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 5.21. Решите уравнение |
2х2 3х 5 |
2х2 3х 5 3х . |
||||||
|
|
|
|
|
|
|||
Решение. Составим уравнение |
|
2х2 3х 5 |
2х2 3х 5 А; |
|||||
умножим исходное уравнение на полученное, тогда
(
 2х2 3х 5 )2 (
2х2 3х 5 )2 (
 2х2 3х 5)2 3Ах; 6х 3Ах.
2х2 3х 5)2 3Ах; 6х 3Ах.
х = 0 не является корнем данного уравнения, в чем можно убедиться непосредственной подстановкой. Имеем А = 2.
|
|
|
|
|
|
|
|
|
|
|
Тогда |
|
2х2 3х 5 |
2х2 3х 5 2. |
|
||||
|
Сложив исходное уравнение и полученное, имеем: |
|
|||||||
|
|
|
|
|
|
|
|||
|
2 2х2 |
3х 5 3х 2; |
8х2 12х 20 9х2 12х 4; |
х2 16; |
|||||
|
х 4, |
Проверка показывает, что только х = 4 удовлетворяет исходному |
|||||||
|
х 4. |
||||||||
|
|
|
|
|
|
|
|
|
|
уравнению. Ответ: 4.
Выполняем задания устно
5.1.Предложите различные методы решения приведенных ниже уравнений:
1)
 x2 8
x2 8 
 2x ;
2x ;
2)
 5x 1
5x 1 
 3x 19 0 ;
3x 19 0 ;
3)
 x 1
x 1
 2x 6 x 3;
2x 6 x 3;
4)x 1 
 x2 x 2 2x 2;
x2 x 2 2x 2;
5)
 3x 1
3x 1 
 x 4 1;
x 4 1;
6)
 3x 4
3x 4 
 x 4 2
x 4 2
 x ;
x ;
7)
 x2 4
x2 4 
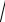 x2 2x 8
x2 2x 8 
 x2 6x 8 ;
x2 6x 8 ;
8)
 2x2 3x 5
2x2 3x 5 
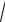 2x2 3x 5 3x ;
2x2 3x 5 3x ;
9)x2 3x 18 4
 x2 3x 6 0 ;
x2 3x 6 0 ;
10)
 x 1
x 1 
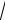 x 3 2
x 3 2
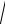 (x 1)(x 3) 4 2x ;
(x 1)(x 3) 4 2x ;
52

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11) |
3 9 |
x 1 3 7 |
|
x 1 4; |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12) |
|
x 3 4 x 1 |
x 8 6 |
x 1 1. |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Практикуемся в решении задач
5.2.Решите уравнение 
 3x 1
3x 1 
 x 4 1 четырьмя способами.
x 4 1 четырьмя способами.
5.3.Решите уравнение 
 x2 4
x2 4 
 x2 2x 8
x2 2x 8 
 x2 6x 8 .
x2 6x 8 .
5.4.Решите уравнение 
 2x2 3x 5
2x2 3x 5 
 2x2 3x 5 3x .
2x2 3x 5 3x .
5.5.Решите уравнение 
 x 1
x 1 
 x 3 2
x 3 2
 (x 1)(x 3) 4 2x .
(x 1)(x 3) 4 2x .
5.6.Решите уравнение 3 9
9 
 x 1 3
x 1 3 7
7 
 x 1 4.
x 1 4.
5.7.Решите уравнение 
 x 3 4
x 3 4
 x 1
x 1 
 x 8 6
x 8 6
 x 1 1.
x 1 1.
Закрепляем материал самостоятельно
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5.8. Решите уравнения: |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x 3)( x2 5x 4 2) 0 ; |
|
||||
1) |
3 x 7 3 |
x 1 2; |
|
|
2) |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 11 x2 11 42 ; |
|
||||
3) |
4 80 x 4 2 x 4 ; |
4) |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
5) |
|
|
21 x |
21 |
x |
|
21 |
. |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
21 x |
21 |
x |
x |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Изучаем интересный материал
Термин «рациональное» (число) происходит от латиноамериканского слова ratio — отношение, которое является переводом греческого слова «логос». В отличие от рациональных чисел, числа, выражающие отношение несоизмеримых величин, были названы еще в древности иррациональными, т. е. нерациональными (по-гречески «алогос»). Правда, первоначально термины «рациональный» и «иррациональный» относились не к числам, а к соизмеримым и соответственно не соизмеримым величинам, которые пифагорейцы называли выразимыми и невыразимыми,
53
Теодор Киренский же — симметричными и асимметричными. В V—VI вв. римские авторы Капелла и Кассиодор переводили эти термины на латынь словами rationalis и irrationalis. Термин «соизмеримый» (commensurabilis)
ввел в первой половине VI в. другой римский автор — Боэций. Древнегреческие математики классической эпохи пользовались
только рациональными числами. В своих «Началах» Евклид излагает учение об иррациональности чисто геометрически.
Математики Индии, Ближнего и Среднего Востока, развивая алгебру, тригонометрию и астрономию, не могли обойтись без иррациональных величин, которые, однако, длительное время не признавали за числа. Греки называли иррациональную величину, например, корень из квадратного числа, «алогос» — невыразимое словами, а позже европейские переводчики с арабского на латынь перевели это слово латинским словом surdus — глухой. В Европе термин surdus впервые появился в середине XII в. у Герарда Кремонского, известного переводчика математических произведений с арабского на латынь. Затем у итальянского математика Леонардо Фибоначчи и других европейских математиков, вплоть до XVIII в. Правда, уже в XVI в. отдельные ученые, в первую очередь итальянский математик Рафаэль Бомбелли и нидерландский математик Симон Стевин, считали понятие иррационального числа равноправным с понятием рационального числа. Стевин писал: «Мы приходим к выводу, что не существует никаких абсурдных, иррациональных, неправильных, необъяснимых или глухих чисел, но что среди чисел существует такое совершенство и согласие, что нам надо размышлять дни и ночи над их удивительной закономерностью».
Еще до Бомбелли и Стевина многие ученые стран Среднего Востока в своих трудах употребляли иррациональные числа как полноправные объекты алгебры. Более того, комментируя «Начала» Евклида и исследуя общую теорию отношения Евдокса, Омар Хайям уже в начале XII в. теоретически расширяет понятие числа до положительного действительного числа. В том же направлении много было сделано крупнейшим математиком XIII в. ат-Туси.
Математики и астрономы Ближнего и Среднего Востока вслед за астрономами Древнего Вавилона и эллинистической эпохи широко пользовались шестидесятеричными дробями, арифметические действия с которыми они называли «арифметикой астрономов». По аналогии с шестидесятеричными дробями самаркандский ученый XV в. ал-Каши в работе «Ключ арифметики» ввел десятичные дроби, которыми он пользовался для повышения точности извлечения корней. Независимо от него, но по такому же пути шел открывший в 1585 г. десятичные дроби в Европе Симон Стевин, который в своих «Приложениях к алгебре» (1594 г.) показал, что десятичные дроби можно использовать для бесконечно близкого приближения к действительному числу. Таким образом, уже в
54

XVI в. зародилась идея о том, что естественным аппаратом для введения и обоснования понятия иррационального числа являются десятичные дроби. Появление «Геометрии» Декарта облегчило понимание связи между измерением любых отрезков (и геометрических величин вообще) и необходимостью расширения понятия рационального числа. На числовой оси иррациональные числа, как и рациональные, изображаются точками. Это геометрическое толкование позволило лучше понять природу иррациональных чисел и способствовало их признанию.
В современных учебных руководствах основа определения иррационального числа опирается на идеи ал-Каши, Стевина и Декарта об измерении отрезков и о неограниченном приближении к искомому числу с помощью бесконечных десятичных дробей. Однако обоснование свойств действительных чисел и полная теория их была разработана лишь в XIX в.
════════════════════════════════════════
Занятие 6. ИРРАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА
══════════════════════════
Актуализируем знания по теме
ОСНОВНЫЕ ВОПРОСЫ
1.Эквивалентные преобразования иррациональных неравенств.
2.Дробно-иррациональные неравенства.
3.Метод интервалов при решении иррациональных неравенств.
4.Замена при решении иррациональных неравенств.
5.Использование монотонности при решении неравенств.
Повторяем теоретический материал
Эквивалентные преобразования иррациональных неравенств
Основным методом решения иррациональных неравенств является метод эквивалентных преобразований. Что подразумевает сведение исходного неравенства к равносильной системе рациональных неравенств.
55

Th.6.1 Неравенство
(x)
систем f (x)
(x)
f (x)

 f (x) (x) равносильно совокупности двух
f (x) (x) равносильно совокупности двух
0,
2 (x),
0,
0.
Th.6.2 |
|
|
|
|
|
|
|
|
(х) 0, |
|
|
|
|
Неравенство |
|
|
|
|
(x) равносильно системе f (x) 0, |
|
|||||
|
|
f (x) |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
(х). |
|
|
|
|
|
|
|
|
|
f (x) |
|
||
Th.6.3 |
|
|
|
|
|
|
|
|
|
f (x) (x), |
||
|
|
|
|
|
|
|
|
|
||||
Неравенство |
|
f (x) (х) |
|
|||||||||
|
|
равносильно системе |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
(x) 0. |
||
Th.6.4 |
|
|
|
|
|
|
|
|
|
(x) 0, |
||
|
|
|
|
|
|
|
|
|
||||
Неравенство |
|
|
(х) 0 |
равносильно системе |
||||||||
|
f (x) |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
f (x) 0. |
||
Th.6.5 |
|
|
|
|
|
|
|
|
|
(x) 0, |
||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
равносильно системе f (x) 0. |
||||||||
|
Неравенство f (x) |
(х) 0 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x ОДЗ. |
||
Дробно-иррациональные неравенства
При решении иррациональных неравенств с дробями сначала стоит избавиться от знаменателя — перейти к эквивалентной совокупности систем неравенств, а уже потом избавляться от радикалов.
|
|
|
|
|
|
|
|
|
|
|
|||||||
Пример 6.1. Решите неравенство |
|
2 x 4x 3 |
2. |
||||||||||||||
|
|
|
|
x |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение. |
|
2 x 4x 3 |
2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
||
|
x 0, |
|
|
|
x 0, |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 x 4x 3 |
2x; |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
2 x 3 2x; |
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
x 0, |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
x 0, |
|
||||||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 x 4x 3 |
2x; |
|
|
|
|
|
|
|
||||||
|
|
|
|
2 x 3 2x; |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Система (1) равносильна совокупности систем (3) и (4):
1
2
56

x 0, |
|
x 0, |
|
||
|
2x 0, (3) |
и |
|
2x 0, |
(4) |
3 |
3 |
||||
|
x 0 |
|
|
2 |
. |
2 |
|
2 |
x (3 2x) |
||
Система из линейных неравенств (3) приводит к двойному
неравенству |
3 |
< х 2, а система (4) — к неравенству 1 |
х |
3 |
. Система |
|||||||
|
|
|||||||||||
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
x 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
x 3 |
2x |
2 |
, x 0 — решение системы (2). |
||||
(2) записывается в виде |
2 |
|
||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
2 |
0, |
|
|
|
|
|
||
|
|
|
|
3 2x |
|
0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Объединяя решения систем (2), (3) и (4), получим решение |
||||||||||||
неравенства. |
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: (– ; 0) |
[1; 2]. |
|
|
|
|
|
|
|
||||
Метод интервалов при решении иррациональных неравенств
Способ предыдущего решения неравенства несколько громоздкий. Здесь удобнее применить метод интервалов, основанный на свойстве непрерывности иррациональных алгебраических функций: любая иррациональная алгебраическая функция, записывающаяся с помощью иррационального алгебраического выражения, непрерывна и, следовательно, сохраняет знак на каждом интервале, содержащемся в области определения этой функции.
Поскольку применение метода интервалов к иррациональным алгебраическим уравнениям основывается не на «идеологии» разложения алгебраических выражений на множители — для иррациональных уравнений она просто не проходит, а на идее использования непрерывности иррациональных алгебраических функций, то схему применения метода интервалов изложим «по шагам».
План решения неравенства методом интервалов
1.Приводим неравенство к виду «сравнения с нулем», используя при этом только равносильные преобразования; если в левой части есть дробные выражения, то приводим их к общему знаменателю.
2.Находим область определения левой части неравенства.
3.Находим и отмечаем на числовой оси все корни соответствующего неравенству уравнения L(х) = 0.
4.Определяем знак левой части неравенства на каждом из промежутков, для чего достаточно вычислить значение L(x) в конкретных (желательно, «удобных»!) точках.
5.Указываем множество решений исходного неравенства.
57

Пример 6.2. Запишем |
неравенство |
из |
предыдущего примера в |
|||||||
|
|
|
|
|
|
|
|
|
x 0, |
|
|
|
|
2 x 2x 3 |
|
|
|
|
|||
стандартном виде: L(x) = |
|
|
|
|
|
0. |
ОДЗ: |
|
. L(x) = 0, если |
|
|
|
|
|
|
||||||
|
|
|
|
x |
|
|
|
x 2 |
|
|
х = 1. Ответ: х (– ; 0) |
[1; 2]. |
|
|
|
|
|
||||
Рис. 7 Преимущество метода интервалов состоит в том, что решение
иррационального неравенства сводится к решению уравнений и к элементарным вычислениям, что, как правило, проще.
Замена при решении иррациональных неравенств
Метод замены в неравенствах используют тогда, когда в неравенство входит только один радикал — корень из линейного выражения от х: если обозначить этот радикал через z, то х записывается в виде многочлена от z.
Пример 6.3. Рассмотрим снова неравенство из предыдущего примера и решим его методом замены.
|
|
|
|
|
|
|
|
|
|
|
|
2 x 4x 3 |
|
|
|
|
z 0 . Тогда |
||
Решение. |
|
2. Пусть |
2 x = z, |
||||||
|
|
|
|
||||||
|
|
x |
|||||||
|
|
|
|
|
|
|
|
||
х = 2 - z2, и неравенство записывается в виде:
z 4(2 z |
2 ) 3 |
2 |
|
4z2 z 5 |
2 |
|
2z2 z 1 |
0 |
R(z) |
||
2 z2 |
|
|
z2 2 |
z2 2 |
|
||||||
|
|
|
|
|
|
|
|
||||
Решив неравенство методом интервалов, получим Выполнив обратный переход, получим результат.
|
(z 1)(2z 1) |
|
|
|
0 . |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(z |
|
2)(z |
2) |
||||||
|
|
|
||||||||
0 |
z 1 и |
|
|
|
|
|||||
|
|
2 < z. |
||||||||
Ответ: х (- ; 0) [1; 2].
Использование монотонности при решении неравенств
Использование монотонности рассмотрим на примере сложного иррационального неравенства.
Пример 6.4. Решим неравенство: 
 x +
x + 
 x 7 + 2
x 7 + 2 
 x(x 7) < 35 - 2x. Решение. Перепишем его в стандартном виде:
x(x 7) < 35 - 2x. Решение. Перепишем его в стандартном виде:
|
|
|
|
|
|
|
|
|||||||||
L(x) = |
x + |
x 7 + 2 |
x(x 7) + 2x – 35 < 0, |
(*) |
||||||||||||
ОДЗ неравенства х ≥ 0, левая часть L(x) строго возрастает на ОДЗ. В |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
самом деле, функции |
u x |
|
и |
|
v |
x 7 |
строго |
возрастают и |
||||||||
неотрицательны на R+, поэтому и третье слагаемое, которое в ОДЗ можно |
||||||||||||||||
|
x x 7 |
|
|
|
|
|
|
|
|
|
|
|
||||
записать в виде 2 |
2 |
|
x |
|
x 7 2uv |
также |
является строго |
|||||||||
возрастающей функцией, как и линейная функция h(x) = 2х - 35; а сумма возрастающих функций также строго возрастает. Вывод: если в какой-то точке х = x0 R+ левая часть неравенства обращается в нуль, то неравенство (*) выполнено для тех и только тех значений х из ОДЗ, для которых х < х0.
58

Итак, чтобы решить неравенство (*), достаточно решить соответствующее уравнение, которое записывается в виде
|
|
|
|
|
|
|
|
L(x) = |
x |
+ x 7 + 2 |
x(x 7) + 2x – 35 = 0 |
|
|||

 x +
x + 
 x 7 + x +(x+7) + 2
x 7 + x +(x+7) + 2 
 x
x 
 x 7 - 42 = 0
x 7 - 42 = 0
( 
 x +
x + 
 x 7 )+ (
x 7 )+ ( 
 x +
x + 
 x 7 )2 – 42 = 0 или z2 + z – 42 = 0, где
x 7 )2 – 42 = 0 или z2 + z – 42 = 0, где
|
|
|
|
|
|
|
|
|
|
x 7 ≥ |
|
|
|
z = x + |
7 |
. |
||||
|
|
|
|
|
|
|
Из квадратного уравнения находим: z = 6 или z = -7. |
||||||
Поскольку корень z = -7 не удовлетворяет ограничению z ≥ 
 7 , приходим к единственному уравнению замены
7 , приходим к единственному уравнению замены 
 x +
x + 
 x 7 = 6. Решив
x 7 = 6. Решив
841 |
|
841 |
|
||||||
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
уравнение, найдем x 144 . Ответ: x |
[0; 144 ). |
|
|||||||
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Практикуемся в решении задач
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6.1. Решите неравенства: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1) |
x2 3x 1 3x 4 ; |
2) |
2x2 3x 5 x 1; |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4) x 3 |
|
|
|
x2 9; |
|
|||||||||
|
|
|
x2 7x 12 6 x ; |
|
||||||||||||||||||||
3) |
|
|
x2 4 |
|
||||||||||||||||||||
5) x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
x2 x 2 |
0 ; |
|
|
|
|
|
|
|
|
|||||||||||||||
6) |
x 2 x 5 x 3 ; |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
7) |
3x2 5x 7 3x2 5x 2 1. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Закрепляем материал самостоятельно
6.2. Решите неравенства:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) |
|
2x 3 |
|
|
x 2 |
; |
|
2) |
|
4 |
|
|
3 |
|
|
x 1 |
; |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
4x 1 |
x 2 |
|
|
|
4 |
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 2x x2 |
3 2x x2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
4 1 x 2 x 0 ; |
|
|||||||||||||||||||||||||||||||||
3) |
|
4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
||||||||||||||
|
|
x |
8 |
|
|
|
|
|
2x 1 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
2x2 15x 17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
5) |
|
0 ; |
6) |
|
|
x |
|
1 |
|
|
x |
|
1 |
|
|
2 |
. |
|
||||||||||||||||||
|
10 x |
|
|
|
|
|
x2 |
|
|
x2 |
|
x |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
59

════════════════════════════════════════
Занятие 7. УРАВНЕНИЯ И НЕРАВЕНСТВА, СОДЕРЖАЩИЕ ЗНАК АБСОЛЮТНОЙ ВЕЛИЧИНЫ
══════════════════════════
Актуализируем знания по теме
ОСНОВНЫЕ ВОПРОСЫ
1.Теоремы об эквивалентных переходах.
2.Общая схема решения уравнений и неравенств с модулями.
3.Специальные соотношения.
Повторяем теоретический материал
Решать уравнения или неравенства с модулем можно одним из основных способов: по определению модуля, исходя из геометрического смысла модуля, возведением обеих частей в квадрат, методом интервалов и графическим способом.
Некоторые уравнения или неравенства можно решить, используя специальные соотношения.
|
|
x, x 0, |
|
f (x), f (x) 0, |
Определение модуля: |
x |
|
f (x) |
|
|
|
x, x 0, |
|
f (x), f (x) 0. |
При решении простейших уравнений и неравенств целесообразно использовать равносильные преобразования.
|
f (x) |
|
a |
f (x) a, |
если a 0 . |
1) |
|
|
|||
|
|
|
|
f (x) a, |
|
|
|
|
|
|
Если a 0, то уравнение решений не имеет.
2) Уравнение вида f (x) g(x) можно решить разными способами:
|
|
|
|
|
g(x) 0, |
1 способ: |
|
f (x) |
|
g(x) |
|
|
|
||||
|
|
f (x) g(x), |
|||
|
|
|
|
|
|
|
|
|
|
|
f (x) g(x). |
60
