
ПРЗ-1_Уравнения и неравенства
.pdf
Изучаем интересный материал
Старинные задачи. Около 2 500 лет назад в Греции уже умели довольно хорошо решать уравнения с одним неизвестным и систему уравнений с несколькими неизвестными. Независимо от греков этими приемами овладели и китайцы, а позднее и индийцы.
Вот несколько старинных задач.
1. Задача в стихах из так называемой «Греческой антологии»
—Скажи мне, знаменитый Пифагор, сколько учеников посещают твою школу и слушают твои беседы?
—Вот сколько, — ответил философ, — половина изучает математику, четверть — музыку, седьмая часть пребывает в молчании и, кроме того, есть еще три женщины.
Решение. Если обозначить число учеников Пифагора через х, то
можно составить такое уравнение: 12 x 14 x 71 x 3 x , откуда x 28.
2. Древняя индусская задача
Два лица имеют равные капиталы, причем каждый состоит из известного числа вещей одинаковой ценности и известного числа монет. Но как число вещей, так и суммы денег у каждого различны. Какова ценность вещи?
Решение. Пусть у первого будет а вещей и т монет, а у второго b вещей и р монет. Если х — ценность вещи, то: ax m bx p , откуда
x p m . a b
3. Английская народная задача, переработанная знаменитым английским ученым И. Ньютоном
Три луга, покрытые травою одинаковой густоты и скорости роста,
имеют площади: 3 13 га, 10 га, 24 га. Первый прокормил 12 быков в течение
4 недель; второй — 21 быка в течение 9 недель. Сколько быков может прокормить третий луг в течение 18 недель?
Решение. При решении задачи надо учесть то обстоятельство, что трава на лугу непрерывно пополняется за счет роста. Если обозначим через у ту долю первоначального запаса травы на 1 га, которая прирастает за
неделю, то на первом лугу в течение недели прирастет травы 3 13 у, а в
течение четырех недель |
3 |
1 |
y 4 13 |
1 |
y |
того запаса, который |
|
|
|||||
|
|
3 |
3 |
|
||
|
|
41 |
|
|
|
|

первоначально на нем имелся. А это равносильно тому, как если бы первоначальная площадь луга увеличилась на 3 13 у га, т. е. сделалась бы
|
|
|
|
3 |
1 |
13 |
1 |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
равной: |
|
|
|
|
га. Другими словами, |
быки |
|
съели |
столько травы, |
||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
13 |
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||
сколько покрывает луг площадью в |
3 |
|
|
|
|
y |
га. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
В одну неделю 12 быков поели |
1 |
|
|
этого количества, а 1 бык в неделю |
|||||||||||||||||||||||||||||||||||||||
|
|
4 |
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
10 40 y |
|
||||
|
|
, т. е. запас, растущий на площади: |
3 |
|
|
13 |
|
|
y : 48 |
|
|
(га). |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
48 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
144 |
|
||||
|
|
Подобным же образом находим площадь луга, кормящего одного |
|||||||||||||||||||||||||||||||||||||||||||
быка в течение недели, из данных для второго луга. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
Недельный прирост на 1 га = у, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
9-недельный прирост на 1 га = 9 у, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
*** |
|
|
|
|
|
|
на 10 га = 90 у. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
Площадь участка, содержащего запас травы для прокормления 21 |
|||||||||||||||||||||||||||||||||||||||||||
быка в течение 9 недель, равна 10 + 90 у. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
Площадь, достаточная для прокормления 1 быка в течение 1 недели: |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 90 y |
|
10 90 y |
. |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 21 |
|
|
|
|
189 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Обе нормы прокормления должны быть одинаковы |
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
10 40 y |
|
10 90 y |
, откуда |
y |
|
1 |
. |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
144 |
|
189 |
|
|
|
12 |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Определим теперь площадь луга, наличный запас травы которого |
|||||||||||||||||||||||||||||||||||||||||||
достаточен для прокормления одного быка в течение недели: |
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 40 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
10 40 y |
|
|
|
|
5 |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
(га). |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
144 |
|
|
144 |
|
|
|
|
|
|
|
|
54 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
Наконец, приступаем к вопросу задачи. Обозначим искомое число |
|||||||||||||||||||||||||||||||||||||||||||
быков через х, тогда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
24 24 18 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
12 |
|
|
|
5 |
, откуда x 36 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
18 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
54 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ответ. Третий луг может прокормить в течение 18 недель 36 быков.
42

════════════════════════════════════════
Занятие 5. МЕТОДЫ РЕШЕНИЯ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ
══════════════════════════
Актуализируем знания по теме
ОСНОВНЫЕ ВОПРОСЫ
1.Равносильные преобразования простейших иррациональных уравнений.
2.Решение иррациональных уравнений методом замены.
3.Использование монотонности функций при решении иррациональных уравнений.
4.Использование однородности при решении иррациональных уравнений.
5.Метод сведения к системе уравнений.
6.Метод оценки левой и правой частей уравнения.
7.Идея сопряженности при решении иррациональных уравнений.
Повторяем теоретический материал
Def. Иррациональными уравнениями называются уравнения, в которых переменная содержится под знаком корня.
Решение иррациональных уравнений сводится к переходу от иррационального к рациональному уравнению путем возведения в степень обеих частей уравнения или замены переменной.
При возведении обеих частей уравнения в четную степень возможно появление посторонних корней. Поэтому при использовании указанного метода следует проверить все найденные корни подстановкой в исходное уравнение.
Следует заметить, что указанный метод целесообразно использовать, когда найденные корни уравнения удобны для проверки.
Рассмотрим решение простейших иррациональных уравнений путем равносильных преобразований.
43

Th.5.1 Уравнение 
 f (x) a не имеет корней, если a 0 , и равносильно уравнению f (x) a2 , если a 0 .
f (x) a не имеет корней, если a 0 , и равносильно уравнению f (x) a2 , если a 0 .
Th.5.2
Th.5.3
Уравнение 
 f (x)
f (x)
следующих систем:
Уравнение 
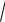 f (x)
f (x)

 g(x) равносильно одной
g(x) равносильно одной
f (x) g(x), |
f (x) g(x), |
|
или |
g(x) 0; |
f (x) 0. |
f (x) g(x) равносильно системе
g(x)
(любой) из
g 2 (x),
0.
Th.5.4 |
|
|
|
|
|
f (x) 0, |
||||
|
|
|
|
|
|
|
|
|
||
|
Уравнение f (x) g(x) 0 равносильно системе |
|||||||||
|
|
g(x) 0, |
||||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
x ОДЗ. |
||
|
Равносильные преобразования могут быть применены и при |
|||||||||
решении уравнений других видов. |
|
|
|
|
|
|
|
|||
|
Пример 5.1. Решите уравнение x 3 |
|
|
|
|
|
||||
|
|
x2 5x 4 2x 6 . |
||||||||
|
Решение. Перепишем уравнение в виде x 3 ( |
|
|
|
||||||
|
|
x2 5x 4 2) 0 . |
||||||||
|
|
|
|
2 |
5x 4 0, |
|||||
|
|
|
x |
|
||||||
|
Перейдем к равносильной системе x 3 0, |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 5x 4 |
|
2. |
||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
Ответ: x 0 или x 5 . |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Пример 5.2. Решите уравнение 2x 3 |
4x 1 4 . |
|
|
|
|
|||
|
|
|
|
|
3 |
|
|
|
Решение. На области допустимых значений уравнения |
|
|
; |
обе |
||||
|
||||||||
|
|
|
|
|
2 |
|
|
|
его части принимают неотрицательные значения. Следовательно, данное уравнение равносильно системе:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( 2x 3 |
4x 1)2 42 , |
|
|
|
|
|
|
|
10x 3 9 3x 2 , |
|||||||
8x |
2 |
10x 3 |
9 3x, |
8x2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
3 |
|
|
|
|
|
3 |
|
|
3x 0, |
||||||
x |
|
|
|
|
|
|
|
|
9 |
|||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|||
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|||||
|
|
|
|
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
x |
. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
Ответ: x 2.
Заметим, что формальное применение теорем о корне, которые часто используются при решении уравнений, нередко приводит к ошибкам. Очень распространенной ошибкой является применение теоремы о корне
44

из произведения в виде: 
 ab
ab 
 a
a 
 b .
b .
На самом деле записанная формула справедлива лишь при a 0 и
b 0 . А если a 0 и b 0 , то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ab |
a b . |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример 5.3. Решите уравнение |
|
4x2 9x 5 |
|
2x2 x 1 x2 |
1. |
|||||||||||||||||
Решение. Разложим подкоренные выражения на множители: |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
. |
|
|
||||||||||||
|
x 1 4x 5 |
x 1 2x 1 |
x 1 x 1 |
|
|
|||||||||||||||||
ОДЗ данного уравнения является множество |
; |
5 |
1 |
1; . |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Поэтому применять теорему нужно на каждом из промежутков отдельно. Таким образом, исходное уравнение равносильно следующей совокупности:
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1 4x 5 x 1 2x 1 x 1 x 1; |
||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
x 1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1 4x 5 |
x 1 2x 1 |
|
x 1 x 1; |
|||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x 1)(4x 5) |
(x 1)(2x 1) |
|
(x 1)(x 1). |
|||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Объединив решения каждой из систем, получим решение уравнения.
Ответ: x = –1 или x = 5.
МЕТОД ЗАМЕНЫ
Зачастую, когда основной метод решения иррациональных уравнений приводит к громоздким преобразованиям, применяют метод замены. Рассмотрим наиболее типичные случаи.
Пример 5.4. Решите уравнение 
 х3 8 4
х3 8 4  х3 8 6.
х3 8 6.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Решение. |
ОДЗ: х -2. Пусть 4 х3 |
8 |
= t, |
t 0. Тогда t 2 + t |
– 6 = 0; |
||||||||||||||
t 2, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Учитывая, что t 0, имеем: t = |
2. Тогда 4 х3 8 |
= 2; х 3 = 8; х = 2. |
||||||||||||||||||
|
|
|||||||||||||||||||
t 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Ответ: 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Пример 5.5. Решите уравнение x2 |
x2 20 22. |
|
|
||||||||||||||||
|
Решение. ОДЗ: х R. Добавим к обеим частям уравнения число 20. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Получим: х 2 + |
20 + х2 20 42 . |
Пусть |
|
х2 20 |
= t, t 0. |
Тогда |
||||||||||||||
|
|
t 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
x2 20 6; |
x 2 +20 = 36; |
x 2 =16; x = 4 или |
|||||||||||||
t 2 +t – 42 = 0: |
|
t = 6. |
||||||||||||||||||
|
|
t 6; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
45

x = –4.
Ответ: 4; - 4.
Пример 5.6. Решите уравнение 
 х2 х 4
х2 х 4 
 х2 х 1
х2 х 1 
 2х2 2х 9. Решение. ОДЗ: х R. Пусть x2 x 1 t (t 0) , тогда получим:
2х2 2х 9. Решение. ОДЗ: х R. Пусть x2 x 1 t (t 0) , тогда получим:
|
|
|
|
|
|
|
|
t 1, |
|
t 3 |
t |
2t 7; |
|
|
|
||||
|
|
|
|||||||
|
t2 3t 2 |
t = 1 (с учетом |
|||||||
|
|
|
|
|
|
|
|
t 4; |
|
условия t > 0). Вернувшись к исходной переменной, получим х = 0 или х = -1. Все преобразования были равносильными. Проверка не требуется.
Ответ: -1; 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 5.7. Решите уравнение |
|
|
х 3 4 х 1 |
х 8 6 |
|
х 1 1. |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
|
(х 1) 4 |
|
х 1 3 1 |
(х 1) 6 х 1 8 1 1; |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Пусть |
х 1 t , |
(t 0); |
тогда |
x 1 t 2 ; x t 2 1. |
Исходное |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
уравнение примет вид: t 2 |
4t 4 |
t 2 6t 9 1; |
|
t 2 |
|
|
|
|
t 3 |
|
1. |
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
I. 00 t t 2;2;t t 22 t t 33 1;1; |
t = 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
II. 2< t 3; t 2 t 3 1; t (2;3] . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
III. t >3; t 2 t 3 1; |
2t = 6; t = 3 — не принадлежит рассмотрен- |
||||||||||||||||||||||||||||||||
ному промежутку. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
||||||||||||||||||||||||||||
Итак, 2 t 3. Отсюда |
2 |
x 1 3; 4 x 1 9; |
|
5 x 10. |
|||||||||||||||||||||||||||||
Ответ: 5; 10 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ИСПОЛЬЗОВАНИЕ МОНОТОННОСТИ ФУНКЦИЙ
Напомним свойства монотонных функций:
а) сумма возрастающих (убывающих) на множестве Х функций также возрастающая (убывающая) функция;
б) если функция y = f(x) возрастает (убывает) на множестве Х, то и функция y = f(x)+ c, где с R также возрастает (убывает) на Х;
в) если функции y = f(x) и y = d(x) возрастают (убывают) на множестве Х и принимают на этом множестве положительные значения, то функция y = f(x)d(x) также возрастает (убывает) на Х.
Свойства монотонных функций позволяют решить многие уравнения
гораздо быстрее. |
|
Пример 5.8. Решите уравнение 17 x |
9 x 4 . |
Решение. Данное уравнение можно решить повторным возведением в квадрат или заменой с ограничением. Однако, самый короткий способ — заметить, что значение х = 8 удовлетворяет уравнению (5 - 1 = 4), а левая
|
|
|
|
|
часть уравнения, т. е. функция L(x) = 17 x - |
9 x , строго возрастает на |
|||
своей области определения (на отрезке [-17; |
9]), ибо является суммой |
|||
L(x) = а(х) + с(х) двух возрастающих функций а(х) = 
 17 х и
17 х и
46

с(х) = - 
 9 х (функция b(x) =
9 х (функция b(x) = 
 9 х — строго убывающая, поэтому с(x) = -b(х) — строго возрастающая). Значит, если х < 8, то L(х) < L(8) = 4, а если х > 8, то L(x) > L(8) = 4, поэтому у нашего уравнения L(x) = 4 единственный корень х = 8.
9 х — строго убывающая, поэтому с(x) = -b(х) — строго возрастающая). Значит, если х < 8, то L(х) < L(8) = 4, а если х > 8, то L(x) > L(8) = 4, поэтому у нашего уравнения L(x) = 4 единственный корень х = 8.
Ответ: х = 8.
Отличительная черта последнего способа решения — его универсальность. Этот способ годится для множества обобщений разобранного уравнения.
Отметим, что вместо оценок (типа x < 8 L(x) < L(8) и т. п.) можно сформулировать, доказать, а затем систематически использовать следующее утверждение.
Th.5.5 (о значениях монотонных функций)
Любая строго монотонная на всей области определения функция каждое свое значение принимает не более чем при одном значении аргумента.
Иными словами, если функция L(x) является строго монотонной на своей области определения D(L) R, то при любом значении c R уравнение L(x) = с имеет не более одного решения.
Отсюда следует, что для решения уравнения L(x) = с достаточно указать (и проверить!) один его корень — (конкретное) значение х = x 0 ;
других корней это уравнение иметь не будет.
Th.5.6 |
(следствие из теоремы 5.5) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Если левая часть уравнения L(x) = R(x) строго возрастает, а правая |
||||||||||||||||||||||||
|
|
часть строго убывает на ОДЗ (области допустимых значений) этого |
||||||||||||||||||||||||
|
|
уравнения (или наоборот, левая часть убывает, а правая часть |
||||||||||||||||||||||||
|
|
возрастает), то данное уравнение имеет не более одного корня. |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Пример 5.9. Решите уравнение |
|
х 7 + 3 х = 3. |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
Решение. ОДЗ: х 7. Очевидно, что |
x 8 |
есть корень данного |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
уравнения. Рассмотрим функцию f(x) = |
х 7 + 3 |
х , |
она возрастает на |
||||||||||||||||||||||
|
[7; + ). Тогда уравнение f(x) = 3 имеет единственный корень х = 8. |
|
||||||||||||||||||||||||
|
|
Ответ: 8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
2 |
. |
|
|
|
|
|
|
|
|
||||||||
|
|
Пример 5.10. Решите уравнение 3 х + 5 |
х |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
ОДЗ: х 0. Рассмотрим функцию f(x) |
|
|
|
|
|
|
|||||||||||||||||
|
|
Решение. |
= 3 |
х + 5 х , |
она |
|||||||||||||||||||||
|
возрастает при |
x 0. Функция |
g(x) = |
|
2 |
|
|
|
убывает |
на |
|
каждом |
из |
|||||||||||||
|
|
х |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
промежутков х (– ; 0) и х (0; + ).
47

На промежутке (0; + ) исходное уравнение имеет корень х = 1, и он единственный, поскольку справедливо утверждение: если в уравнении f(x)= g(x) функция f(x) возрастает на определенном промежутке, а функция g(x) убывает на этом же промежутке, то это уравнение может иметь не больше одного корня на рассмотренном промежутке.
Рассмотрим теперь промежуток (- ; 0). На нем корень данного уравнения х = -1, и он единственный. Значит, исходное уравнение имеет два корня х =1 и х = -1.
Ответ: 1; -1.
ИСПОЛЬЗОВАНИЕ ОДНОРОДНОСТИ
Соображения однородности при решении уравнений с одной переменной х могут быть использованы в случае, когда то или иное уравнение записывается как однородное относительно каких-то двух новых переменных и = и(х), v = v(x).
|
|
|
|
|
|
|
Пример 5.11. Решите уравнение 3 (х 1)2 + 3 (х 1)2 |
= 2 3 х2 1 . |
|||||
Решение. Если данное уравнение переписать |
в переменных |
|||||
и = 3  х 1, v = 3
х 1, v = 3  х 1 , то получится однородное уравнение второй степени: и2 + v2 = 2uv (*). Его можно решать по стандартной схеме для однородных уравнений:
х 1 , то получится однородное уравнение второй степени: и2 + v2 = 2uv (*). Его можно решать по стандартной схеме для однородных уравнений:
(*) { и = о и v = 0} { uv = k и 1 + k2 = 2k}.
Однако в данном конкретном случае (когда справа стоит коэффициент 2!) проще записать уравнение (*) в виде (и – v)2 = 0 и = v;
соответственно, 3  х 1 = 3
х 1 = 3  х 1 x 1 x 1 2 = 0 . Ответ: нет решений.
х 1 x 1 x 1 2 = 0 . Ответ: нет решений.
Пример 5.12. Решите уравнение 2 3  (х 1)2 + 3
(х 1)2 + 3  (х 1)2 = 3 3
(х 1)2 = 3 3  х2 1 .
х2 1 .
Решение. Данное уравнение тоже относится к однородным уравнениям в указанном выше смысле. Для его решения можно сразу «рассмотреть случаи».
Если х +1 = 0, то подстановка в уравнение значения х = -1 приводит к числовому равенству 0 + 3  8 = 0, которое, очевидно, не выполняется.
8 = 0, которое, очевидно, не выполняется.
Значит, в этом случае решений нет. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
В |
случае |
x 1 0 , |
делим обе |
части |
уравнения |
на |
выражение |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
3 |
|
х 1 |
|
= 3 |
|
х 1 |
|
|
|
|
|
|
|
||
3 (х 1)2 |
, вводим новую |
переменную |
= k |
и |
решаем |
||||||||||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
х 1 |
|||||||||||||||||
|
|
|
|
|
|
3 |
|
х 1 |
|
|
|
|
|
|
|
||||||
получающееся уравнение относительно k: 2 + k2 = 3k |
k2 – 3k + 2 = 0 |
|
|||||||||||||||||||
k = 1 и |
k = 2. |
Далее переписываем |
уравнение замены, |
3 |
|
|
х 1 |
= k |
|
||||||||||||
|
|
х 1 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
48
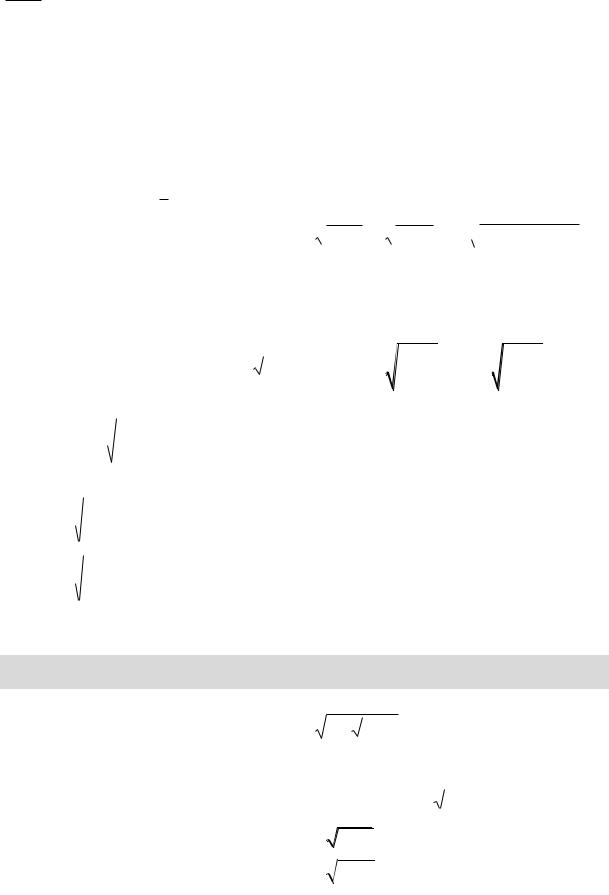
х1
х1
= k 3 , и решаем его для найденных значений k. |
|
|
|||||||
а) Для k = 1, как и в предыдущем примере, |
|
|
|
||||||
|
х 1 |
= 1 |
х 1 х 1, |
|
2 0, |
|
. |
||
|
|
|
|
|
|
||||
|
х 1 |
1 |
|||||||
|
|
х 1 0 |
|
х |
|
|
|||
б) Если k = 2, то |
|
|
|
|
|
|
||||
|
х 1 |
|
х 1 8х 8, |
7х 9, |
x = - |
9 |
|
|||
|
|
|
=8 |
|
|
|
|
|
. |
|
|
х 1 |
х 1 0 |
х 1 |
7 |
||||||
|
|
|
|
|
|
|||||
Ответ: х = - 97 .
Пример 5.13. Решите уравнение 3  х 3 + 3
х 3 + 3  х 2 = 5 6
х 2 = 5 6  (х 2)(х 3) .
(х 2)(х 3) .
Решение. Уравнение тоже относится к однородным уравнениям в указанном выше смысле. ОДЗ: х ( ; 2] [3; + ).
Убедимся, что х = 2 не является корнем данного уравнения (путем непосредственной подстановки значения х = 2 в исходное уравнение).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 3 |
|
1 5 3 |
x 3 |
|
1. |
|||||||||||||||||
Делим обе части уравнения на 3 |
|
х 2 . Имеем 6 3 |
|
|
||||||||||||||||||||||||||||||||||||
x 2 |
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
, |
|
|
|
|
|
|
|||
|
|
|
|
|
|
х 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||
|
Пусть 6 |
|
|
|
= t , t ≥ 0. Тогда 6t 2 - 5t + 1 = 0; |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
х 2 |
|
|
1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
. |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 3 |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
1) |
6 |
|
х 3 |
= |
|
1 |
; |
= |
|
1 |
; 64x – 192 = x – 2; 63x = 190; x = |
190 |
. |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x 2 |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
х 2 |
|
|
|
2 |
|
|
|
|
64 |
|
|
|
|
|
|
|
|
|
|
|
|
63 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x 3 |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
2) |
6 |
|
х 3 |
= |
|
1 |
; |
|
= |
|
1 |
|
|
; 729x – 2187 = x – 2; 728x = 2185; |
|||||||||||||||||||||||||
|
|
х 2 |
|
3 |
x 2 |
729 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
x = |
2185 |
. Ответ: |
190 |
; |
2185 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
728 |
|
728 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
63 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
СВЕДЕНИЕ К СИСТЕМЕ
Сначала разберем пример, к которому применима неполная замена.
|
|
|
|
|
||
Пример 5.14. Решите уравнение 1 1 х = х. |
|
|
||||
Решение. |
Если решать данное |
уравнение |
последовательным |
|||
возведением в |
квадрат, то получится |
не слишком привлекательное |
||||
|
|
|
||||
уравнение степени 4. Введем новую переменную |
1 х = у, оставив и |
|||||
1 x y,
переменную х, — перейдем к системе: 
 1 y x
1 y x
1 х у 2 ,
1 у х2 , (*).х 0, у 0
49

Получающаяся рациональная |
алгебраическая |
система допускает |
|||||
х у 2 |
1, |
(1) |
(1) (2) : х у у 2 |
х 2 , |
|||
разложение: |
|
|
|
|
|
|
|
у х 2 |
1 |
(2) |
|
(2) : |
у х 2 1 |
|
|
( у 2 |
х 2 ) ( у х) 0, |
( у х)(у х 1) 0, |
|||||
|
у х2 |
1, |
|
|
у х 2 1, |
|
|
|
|
|
|
||||
|
у х, |
|
|
|
у х |
2 |
1, |
(*) |
|
||
|
х 0, у 0 |
||
|
|||
y x 1 0, или y x2 1,
x 0, y 0.
Решив системы, найдем решение уравнения.
Ответ: х =1  5 ., 2
5 ., 2
Пример 5.15. Решите уравнение 4  41 х 4
41 х 4  41 х 2 .
41 х 2 .
Решение. Для решения данного уравнения можно ввести переменные 4  44141 х х а,а4, 4141 х х bb, — получим систему рациональных
44141 х х а,а4, 4141 х х bb, — получим систему рациональных
a b 2,
уравнений
x4 b4 82.
ОЦЕНКА ЗНАЧЕНИЯ ЛЕВОЙ И ПРАВОЙ ЧАСТИ
Заметим, что если необходимо решить уравнение вида f(x)=g(x) и утверждается, что f(x) a, g(x) a, то равенство достигается только в случае, если f(x) и g(x) одновременно равны a.
Пример 5.16. Решите уравнение 
 х2 7х 6 =12х - х 2 - 36. Решение. Запишем уравнение в виде:
х2 7х 6 =12х - х 2 - 36. Решение. Запишем уравнение в виде: 
 х2 7х 6 = - (х-6) 2 .
х2 7х 6 = - (х-6) 2 .
f(x)= 
 х2 7х 6 0, g(x)= - (x - 6) 2 0. Значит исходное уравнение
х2 7х 6 0, g(x)= - (x - 6) 2 0. Значит исходное уравнение
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х2 7х 6 0, |
|
|
|
|
|
|
|||||||||||
равносильно системе |
(х 6) 0. |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Из второго уравнения системы получим х = 6, что удовлетворяет и |
||||||||||||||||
первому уравнению. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Ответ: 6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
Пример 5.17. Решите уравнение |
60 х 32 5 х |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
40 х 31 . |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Решение. ОДЗ: |
|
х 32 . Определим, что |
при х 32 |
имеем |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
5 х 5 32 2 и левая часть исходного уравнения не меньше 2; 40 |
x 31 1 |
|||||||||||||||||
и правая часть уравнения не больше 2. Значит, х = 32 — корень уравнения, что и подтверждается проверкой.
50
