ПРЗ-1_Уравнения и неравенства

этих случаях могут появиться «посторонние» корни. Очень опасно применять формулы 6)—8) слева направо: из-за сужения ОДЗ уравнений можно потерять их корни.

Например, при переходе от уравнения х(х 1) 0 к уравнению

х х 1 0 теряется корень х = 0. Потеря корня происходит в результате сужения ОДЗ исходного уравнения. ОДЗ исходного уравнения — это множество (- ; 0] [1; + ), а ОДЗ второго уравнения — [1; + ). Таким образом, при замене первого уравнения вторым теряется корень из промежутка (- ; 0].

3. Возведение уравнений в степень

Возведение обеих частей уравнения в квадрат приводит к уравнению-следствию, т. е. при выполнении этой операции могут появиться «посторонние» корни. «Посторонние» корни в этом случае могут принадлежать ОДЗ уравнения.

Если же в обеих частях уравнения стоят функции, принимающие неотрицательные значения на некотором множестве М, то возведение обеих частей уравнения в четную степень приводит к уравнению, равносильному исходному на множестве М.

Замечание. Иногда при решении уравнений вида f(х) (х) = g(х) (х)

его сокращают на общий множитель — функцию (х). При таком «решении» можно как потерять, так и приобрести «посторонние» корни.

С уравнением вида f(х) (х) = g(х) (х) обычно поступают так:

1)переносят все члены уравнения в одну часть;

2)выносят общий множитель за скобки: (х) (f(х) – g(х)) = 0;

3)решают полученное уравнение, как уравнение вида f1(х) f2(х) = 0,

где f1(х) = (х), f2(х) = f(х) – g(х).

СОВЕТЫ:

1.При решении уравнения необходимо внимательно следить за каждым переходом от одного уравнения к другому.

2.Переходить можно либо к равносильному уравнению, либо к уравнению-следствию.

3.В случае перехода к уравнению-следствию необходима проверка найденных корней. Она является неотъемлемой частью решения уравнения.

4.При решении уравнения необязательно искать ОДЗ.

Например, если сводить иррациональное уравнение к следствию, а затем сделать проверку, то нахождение ОДЗ — лишняя работа. Эта работа может нанести даже вред, если забыть, что в этом случае недостаточно сделать проверку на принадлежность корня ОДЗ уравнения. Для некоторых уравнений найти ОДЗ сложнее, чем решить само уравнение

(например, 1 хх2 24 х 1).

11

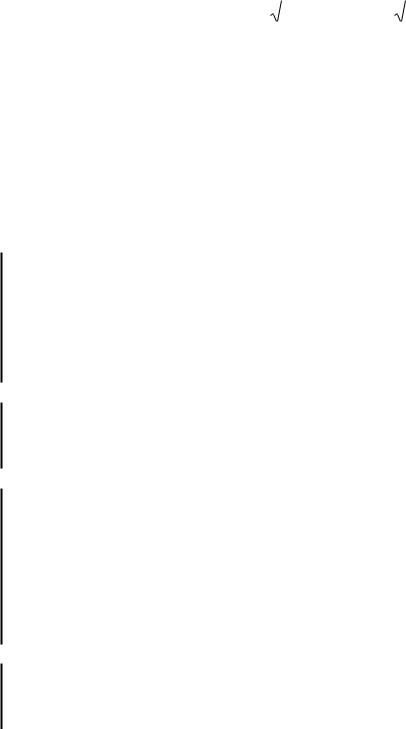
5. В ряде случаев нахождение ОДЗ полезно.

В некоторых случаях знание ОДЗ может упростить решение. Так, встречаются уравнения, ОДЗ которых состоит из нескольких точек или даже есть пустое множество. В этих случаях знание ОДЗ сразу приведет к

x 1. Легко проверить, что x 1 будет корнем нашего уравнения. Знание ОДЗ может упростить:

а) решение уравнения; б) выполнение проверки: если полученное число не принадлежит

ОДЗ, оно не является корнем уравнения.

Теоремы о равносильности уравнений

Th.1.1 Если к обеим частям данного уравнения прибавить (или из обеих частей вычесть) одно и то же число, то получим уравнение, равносильное данному.

Если к обеим частям уравнения прибавить выражение, имеющее смысл во всей ОДЗ данного уравнения, то получится уравнение, равносильное данному.

Th.1.2 Если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный, то получим уравнение, равносильное данному.

Th.1.3 Если обе части уравнения умножить (разделить) на одно и то же число, отличное от нуля, то получим уравнение, равносильное данному.

Если умножить обе части уравнения на отличное от нуля число a или на выражение C(x) , которое при всех допустимых значениях x

имеет смысл и не обращается в нуль, то получим уравнение, равносильное данному.

Th.1.4 Возведение обеих частей уравнения в нечетную степень, а также извлечение корней нечетной степени из обеих частей уравнения приводит к равносильному уравнению.

12

1.2.Существует ли уравнение, следствием которого является любое уравнение?

1.3.Какие из пар уравнений являются равносильными? Какое из уравнений в паре является следствием другого?

1.4. Как может измениться (расшириться или сузиться) множество корней данного уравнения, если:

1) уравнение ( x 3) f (x) 2 x 6 заменить уравнением f (x) 2 ;

1.5. Поставьте между приведенными ниже парами уравнений один из знаков , , .

1)f 2 (x) g2 (x), f (x) g(x) ;

2)f (x) g(x) g(x), f (x) 0 ;

3) f (x)g(x) (x); f (x) g(x) (x);

4)f (x) g(x), f 3 (x) g3 (x) ;

7) (x) f (x) (x)g(x), f (x) g(x) ;

1.6. Укажите, какие из следующих преобразований, примененные слева направо, могут сузить область определения уравнения:

14

Практикуемся в решении задач

15

1.14. Дана функция f (x) 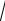х . Среди ниже приведенных функций

подберите такую, чтобы:

1) уравнения f (x) 0 и f (x)g(x) 0 были равносильными;

2)уравнение f (x) 0 являлось следствием уравнения f (x)g(x) 0 ;

3)уравнение f (x)g(x) 0 являлось следствием уравнения f (x) 0 .

1.15. Составьте уравнение, равносильное данному:

х а 0,

5) (x a) х 1 0 и 6) х(х а) 0 и х х а 0 ?

х 1 0;

Закрепляем материал самостоятельно

1.17. Будет ли уравнение, полученное в результате указанного преобразования, равносильно данному:

1) в уравнении 3(2x 1) 5(4x 2) 1 раскрыть скобки и привести

на нуль;

3)в уравнении x2 1 3x 5 0 сократить дробь;

x1

4)обе части уравнения x3 x разделить на x ;

5)обе части уравнения (x 1)(x2 4) x2 4 разделить на x2 4 ;

16

1.18. Какое из двух уравнений является следствием другого?

Изучаем интересный материал

Решение задач методом составления уравнения зародилось давно. Еще 4 000 лет назад в древнем Египте решали задачи способом, который очень напоминает составление уравнения. Недостатком всей математики древних было отсутствие единой математической символики. Этот недостаток затруднял действия, мешал их наглядности. Поэтому и условие, и решение любой задачи приводилось полностью в словесной форме. Правда, у древних египтян были некоторые условные сокращения. Неизвестное, как полагают, они называли «куча». Так, в папирусе Ринда

17

так, как показано на рис. 2. На рис. 3 можно увидеть иероглифическую запись числа 35 736. Эти частичные сокращения были впоследствии забыты другими учеными.

Решение уравнений в Древней Греции и Индии. В

«геометрической алгебре» древних греков решение уравнений сводилось к построению отрезков, представляющих положительные корни уравнений. Зачатки новой, арифметической алгебры встречаются лишь у Диофанта. Вот пример задачи из «Арифметики» Диофанта: «Если прибавить к 20 и отнять от 100 одно и то же число, то полученная сумма будет в 4 раза больше полученной разности. Найти неизвестное».

В1881 году была найдена зарытая в земле близ Бахшали (северозападная Индия) рукопись неизвестного автора, которая, как полагают, относится к VI—VIII вв. В этом памятнике, написанном на березовой коре

иизвестном в настоящее время под названием «Бахшалийской рукописи», содержится такая задача: «Из четырех жертвователей второй дал вдвое больше первого, третий — втрое больше второго, четвертый — вчетверо больше третьего, а все вместе дали 132. Сколько дал первый?».

Вверхней строке на рис. 4 записано уравнение x3 8 x2 16 x3 .

Рис. 4 — Лист из Арифметики (рукопись XIV в.)

18

════════════════════════════════════════

Занятие 2. МЕТОДЫ РЕШЕНИЯ РАЦИОНАЛЬНЫХ УРАВНЕНИЙ

══════════════════════════

Актуализируем знания по теме

ОСНОВНЫЕ ВОПРОСЫ

1.Нахождение целых и рациональных корней уравнений высших степеней.

2.Метод неопределенных коэффициентов.

3.Метод замены.

 Повторяем теоретический материал

МЕТОДЫ РЕШЕНИЯ РАЦИОНАЛЬНЫХ УРАВНЕНИЙ

 Алгебраические уравнения с одним неизвестным. Уравнения

первой степени

Уравнение первой степени с одним неизвестным является частным случаем алгебраического уравнения первой степени (или линейного) ax b 0, a 0 , которое во множестве действительных чисел всегда имеет

решение и притом только одно: x ba .

 Уравнения второй степени (квадратные уравнения)

Алгебраическое уравнение второй степени записывается в общем

19

Отсюда следует, что в качестве целых корней необходимо испытать не какие-либо произвольные целые числа, а лишь делители свободного члена уравнения, которых имеется лишь конечное множество.

Пример 2.1. Решите уравнение x3 4x2 27x 90 0 .

Решение. Выписываем делители свободного члена 90:

1, 2, 3, 5, 6, 9,...

Подставляя эти числа в уравнение, находим, что корнем данного уравнения служит число x 3 . Многочлен, расположенный в левой части уравнения, по теореме Безу должен без остатка делиться на двучлен x 3 . Проделав деление, получим в частном квадратный трехчлен x2 x 30 . Его два корня присоединим к ранее найденному корню и таким образом найдем все три корня данного уравнения: x1 3, x2 5, x3 6 .

которое уже имеет старший коэффициент, равный единице, и к которому применим способ отыскания целых корней, указанный выше. Целые корни для y дадут рациональные, вообще говоря, дробные корни для x .

20