
алгебра функції
.docГрафіки показникової функції і логарифмічної функції, які мають однакові основи, симетричні відносно прямої
у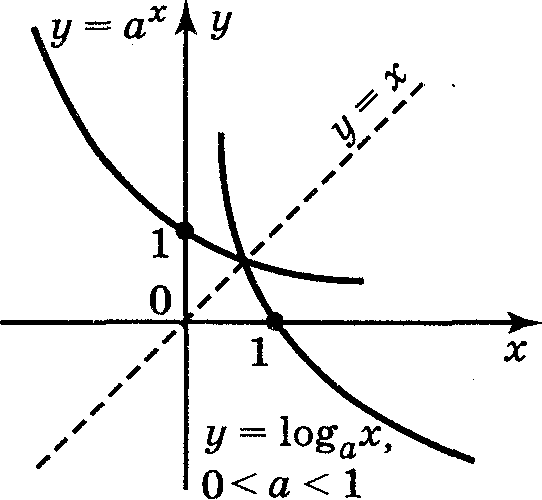 = х
, бо функції у
= ах
і у
= loga
x
є взаємнооберненими.
= х
, бо функції у
= ах
і у
= loga
x
є взаємнооберненими.
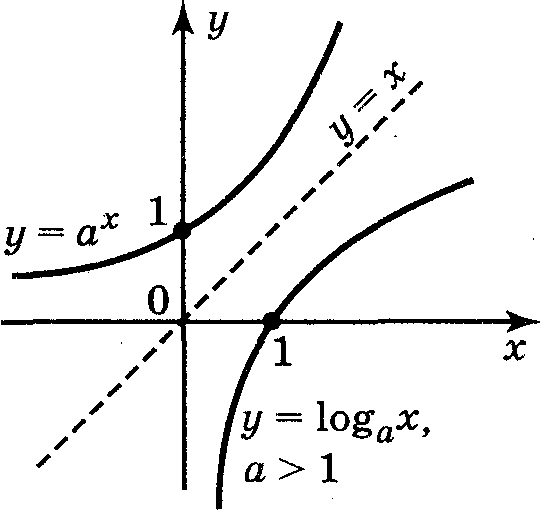
|
Логарифм числа. Основна логарифмічна тотожність |
|
|||||||||
|
Р логарифмом числа b за основою a і позначається logab. Наприклад: 2х = 8; х= 3, тобто log2 8 = 3. Логарифмом додатного числа b за основою а, де а > 0, а ≠ 1, називається показник степеня, до якого треба піднести число а, щоб одержати число b.
Н
log2
log7l = 0, оскільки 70 = 1. lg - десятковий логарифм зосновою 10 ln - натуральний логарифм з основою е ( е = 2,718281828459045...) Дія знаходження логарифма числа (виразу) називається логарифмуванням. Потенціювання — знаходження числа (виразу) за його логарифмом.
Основна
логарифмічна тотожність
|
|
|||||||||
|
Властивості логарифмів |
|
|||||||||
|
Для будь-яких а > 0, а ≠ 1 і будь-яких додатних х і у виконуються рівності: |
Приклади застосування |
Самостійне опрацювання |
|
|||||||
|
1 |
logа l = 0 |
log6 18 + log6 2 = log6(18 – 2) = log6 36 = 2;
log12
48 – log12
4 = log12
log3
log125
5 = log53
5 =
у
=
= 2 lga + 2 lg b – 3 lg c |
Обчисліть:
12. |
|
||||||
|
2 |
logаa = 1 |
|
||||||||
|
3 |
logа xy = logа x + logа y |
|
||||||||
|
4 |
logа
|
|
||||||||
|
5 |
logа
х
р
=
p
logа
x
(р
|
|
||||||||
|
6 |
|
|
||||||||
|
7 |
|
|
||||||||
|
8 |
loga
x
=
|
|
||||||||
|
Логарифмічні рівняння та нерівності |
|
|||||||||
|
Логарифмічними рівняннями називають рівняння, які містять змінну під знаком логарифма. Розв'язати логарифмічне рівняння — це означає знайти всі його корені або довести, що рівняння коренів не має. |
|
|||||||||
|
Види найпростіших логарифмічних рівнянь при a > 0, а ≠ 1, х > 0 |
Приклади розв’язування |
|
||||||||
|
ах = b, b > 0 х= logab |
1.
log3
(2x
+ 1) = 2.
ОДЗ:
2x
+ 1> 0;
x>- 2х + 1 = 32, 2х = 8, х = 4. Відповідь: 4. 2. log3x = log3(6 – х2). х = 6 – х2; х2 + х – 6 = 0; х1 = -3 - не є коренем даного рівняння , х2 = 2. Перевірка: log3x = log32; log3(6 – х2) = log3(6 – 22) = log32. Відповідь: 2. 3. logх+1 (2х2 + 1) = 2. ОДЗ: x+1≠ 1; x≠ 0 2х2 + 1 = (х + 1)2; 2х2 + 1 = х2 + 2х + 1; х2 – 2х = 0; х1 = 0, х2 = 2. Відповідь: 2. |
Методи розв’язання рівнянь 1. Метод зведення до квадратного
log log2 x = у; у2 – 3y = 4; у2 – 3у – 4 = 0; у1 = 4; у2 = -1. Звідси log2 x = 4, log2 x =-1
x
=
16,
x
=
2. Метод зведення логарифмів до однієї і тієї ж основи.
log3
х
– 2
log3
х
– 2 ·
Перевірка:
log3
3 – 2 Отже, х = 3 — корінь. Відповідь: 3 3. Метод потенціювання. log5(x – 1) + log5(x – 2) = log5(x + 2). log5((x – 1)(х – 2)) = log5(x + 2); (х – 1)(х – 2) = х + 2; x2 – 2х – х + 2 = х + 2; x2 – 4х = 0; х(х – 4) = 0; х1 = 0 або х2 = 4. Перевірка (зроби самостійно) Відповідь: 4. 4. Метод логарифмування. х lgx = 100х. lgx lgx = lg(100x); lgx lgx = lg 100 + lgx; lg2x – lg x – 2 = 0.(див. метод 1.) Відповідь: 0,1; 100. |
|
|||||||
|
loga х = b х = аb |
|
|||||||||
|
logx
a
= b,
х
≠
1
хb
= а
х
=
|
|
|||||||||
|
loga x = loga b х = b, b > 0 |
|
|||||||||
|
Самостійне опрацювання |
|
|||||||||
|
log5 x = 2 log2(-x) = -3 lg(2x+1) = lg x lg(x+1) = lg(x+1) log x+1 2 = 1 |
log3 x < 4
log log x-3(х – 1) < 2 |
|
||||||||
|
В розв’язанні логарифмічних нерівностей лежать в основі властивості монотонності логарифмічної функції |
log0,5(x2 + х) > -1. Розв’язання через те, що - 1 = log0,50,5-1 = log0,52, то log0,5(x2 + х) > log0,52. Одержана нерівність рівносильна системі
Розв'язком першої нерівності є
(- Розв'язком другої нерівності є [-2; 1].
Відповідь:
x
|
|
||||||||
|
Якщо а > 1, тоді logaf(x) > logag(x)
рівносильна
системі нерівностей:
|
|
|||||||||
|
Якщо
0 < а
<
1,
тоді logaf(x)
> logag(x)
рівносильна
системі
нерівностей:
|
|
|||||||||
|
Показникові рівняння та нерівності |
||||||||||
|
Показниковими називаються рівняння, у яких невідоме міститься в показнику степеня при постійних основах. Найпростішим показниковим рівнянням є рівняная ах = b, де а > 0, а ≠ 1, рівняння має один корінь, якщо b > 0 і не має коренів, якщо b < 0. Для того щоб розв'язати рівняння, треба b подати у вигляді b = аc, тоді будемо мати аx = ac, звідси х = с |
||||||||||
|
Способи розв'язування показникових рівнянь |
Приклади розв’язання рівнянь |
Приклади розв’язання нерівностей |
||||||||
|
1. Спосіб приведення рівняння до спільної основи, тобто до рівняння виду
2х · 5х = 0,1(10 х – 1)3. (2 · 5)х = 0,1·10 3х – 3; 10х = 10-1 · 103х – 3; 10х = 103х – 4; х = 3х - 4; х = 2. Відповідь: 2. 2. Спосіб винесення спільного множника за дужки. 3х - 2 · 3х – 2 = 63. 3х – 2(32 – 2) = 63; 3х – 2 · 7 = 63; 3х – 2 = 9; 3х-2 =32 ; х – 2 = 2; х = 4. Відповідь: 4. 3. Спосіб приведення рівняння до квадратного. 49х – 8 · 7х + 7 = 0. (72)x – 8 · 7х + 7 = 0; (7х)2 – 8 · 7х + 7 = 0. Нехай 7х = t>0, тоді t2 – 8t + 7 = 0; t1 = 7; t2 = 1. 1) 7х = 7; х = 1; 2) 7х = 1; 7х = 70; х = 0. Відповідь: 1; 0. 4. Графічний спосіб розв'язування показникових рівнянь.
Б
у
=
Вони перетинаються в точці х = 0 Відповідь: х = 0.
|
1. 5х = 125. 5х = 125, 5х = 53, х = 3.
2.
3. 52х – 1 – 52х + 22х + 22х + 2 = 0. 22х + 22х + 2 = 52х +52х – 1 ;
22x(1+
22)
= 52х(1
– 5–1);
22х
· 5 = 52х
·
5 2х = 2; x = l. Відповідь: 1. 4. 3 · 16х + 2 · 81х = 5 · 36х.
3
· 42x
+ 2 · 92x
= 5 · 4х
· 9х:92х;
тоді
3 y2
– 5y
+ 2 = 0, звідси y1
=
Отже:
1)
|
Приклад 1. 3x < 27. 3х < 33. (3 > 1, то функція зростає) х< 3. Відповідь: х (-;3)
Приклад
2.
х
Знак
нерівності змінюється!
Відповідь:
х
(-;-
Приклад
3.
ч х2 + 2х > 3. х2 + 2х – 3 > 0; х1 =-3; х2 =1.
Відповідь:
(- Приклад 4. 25х +25 ∙ 5x – 1250 > 0.
5 t < -50 або t > 25. 5х < -50 або 5х > 25. 1) 5x < -50 — розв'язків немає; 2) 5x > 25; 5x > 52; х > 2. Відповідь: х > 2. |
||||||||

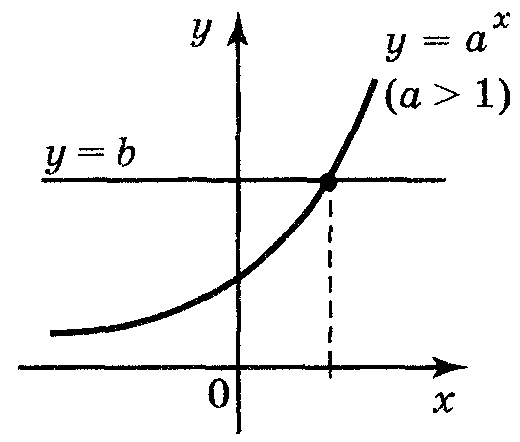 івняння
ах
= b,
де a
>
0, а
≠
1, b
> 0
має єдиний корінь, який називається
івняння
ах
= b,
де a
>
0, а
≠
1, b
> 0
має єдиний корінь, який називається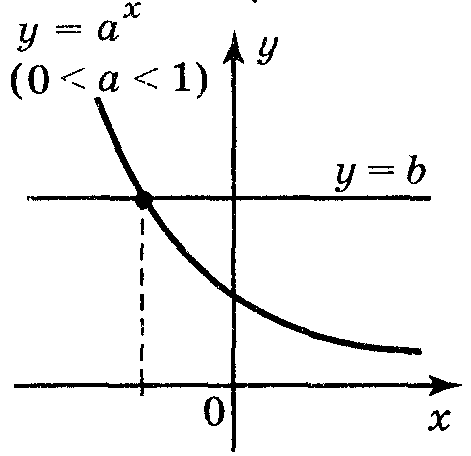 априклад:
log28
= 3, оскільки 23
= 8;
априклад:
log28
= 3, оскільки 23
= 8;
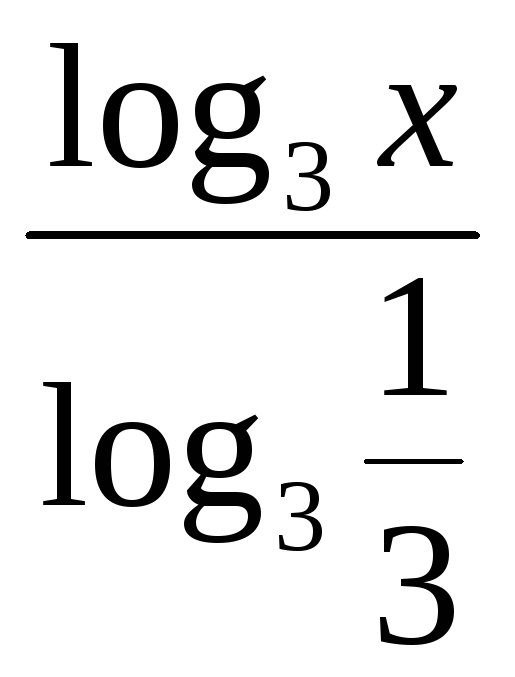 = 3; log3
x
–
2·
= 3; log3
x
–
2·
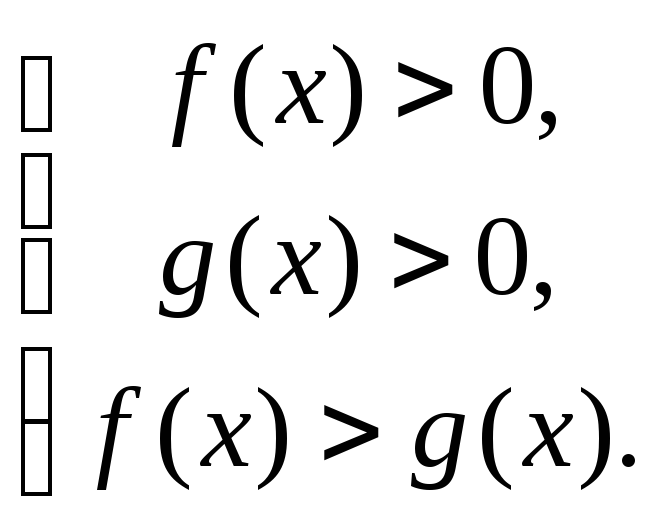
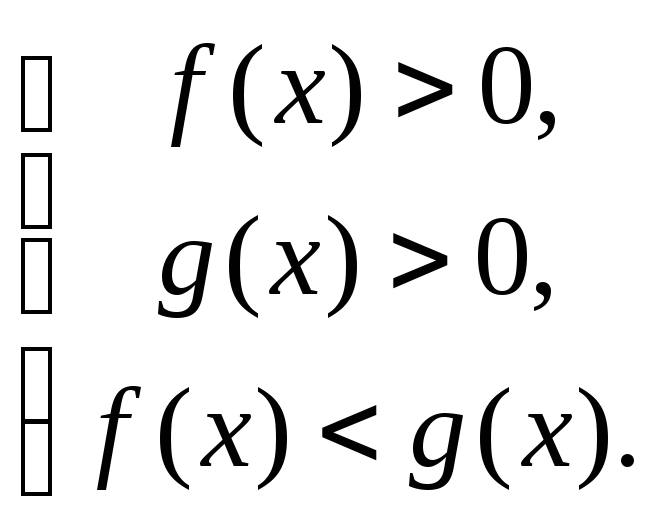
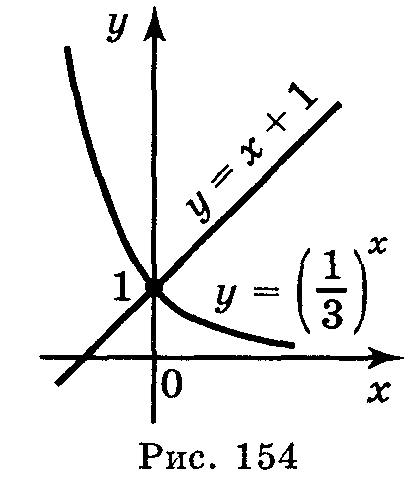 удуємо
графіки функцій
удуємо
графіки функцій