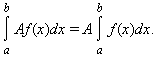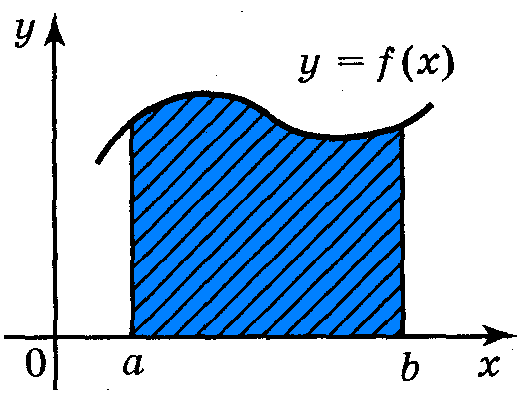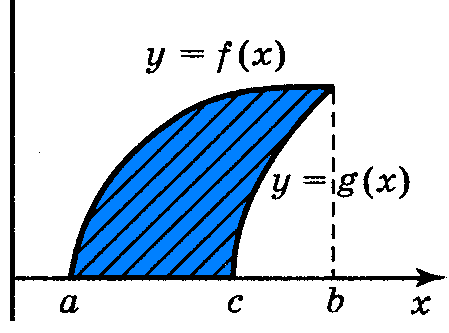алгебра похідна інтеграл
.doc|
Поняття про похідну функції |
||
|
х Δх = х – х0- приріст незалежної змінної( приріст аргументу) в точці х0 х = Δх + х0 f(х) – f (х0) = f(Δх + х0) – f(х0) –приріст функції ∆f = f(Δх + х0) – f(х0) f(х) = f(Δх + х0) = f(х0)+ ∆f Похідною функції f у точці х0 називається число, до якого прямує різницеве відношення
Приклад. Знайти похідну функції f(х) = х3 в точці х0 Розв’язання
|
||
|
Геометричний зміст похідної |
Фізичний зміст похідної |
|
|
П y = f (x) у цій точці:
f′
(x0)
= tgα >0 f′ (x0)
= tg α <0
f′
(x0)
= tgα = 0
|
Якщо точка рухається уздовж осі х і її координата змінюється за законом S(t), то миттєва швидкість точки:
v(t)
=
а прискорення:
а(t)
=
Приклад: точка рухається прямолінійно по закону s(t) = 5t3+ t+3. Знайти v(t) та а(t) в момент часу t = 2 с. v(t) = 15t2 + 1; v(2)= 1522+1=61(м/с) а(t) = 30t; а(2) = 302=60(м/с2)
|
|
|
Рівняння дотичної до графіка функції y = f (x) в точці х0: y = f (x0)+ f′ (x0)(x - x0) |
||
|
Приклад
знаходження рівняння дотичної до
графіка функції f (x) =
1)f
(x0)
= f (1) = 1; 2)f′ (x) = ( |
||
|
|
|
|
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
Таблиця похідних елементарних функцій |
|||||||
|
с' = 0, де с - const |
(xα)′ = αxα-1 |
(kх+b) ′ = k,
|
( |
(lnx)′=
|
(sinx)′= cos x |
(loga
x)′= |
(arcsinx)′=
|
|
(kх) ′ = k, де с - const |
(ex)′ = ex |
(tg
x)′= |
(ctg
x)′= |
(ax)′ = ax lna |
(cosx)′= - sinx |
(arctgx)′= |
(arccosx)′=
-
|
|
Правила диференціювання |
Приклади застосування таблиці та правил знаходження похідних |
|
Якщо у функцій u(х) і v(х) існують похідні, то
|
f′(x)=((x–1)(х+2)cosx)'=(x–1)'(x+2)cosx+(x–1)(x+2)'cosx+(x–1)(x+2)·(cosx)' = =1·(x+2)cosx+(x–1)·1·cosx+(x–1)(x+2)·(–sinx)=(x+2)cosx+(x–1)cosx-(x–1)(x+2)sinx= =(2x+1)cosx-(x-1)(x+2)sinx.
6.
f′ (x)
=
|
|
Похідна складеної функції |
|
|
Якщо у = f(g(x)) і існують похідні f′g і g′x, то у′х = f′g * g′x, де індекси g і x вказують, за яким аргументом обчислюються похідні. Наприклад, f (x) = (3-5х)5 , тут f (g(x)) = (g(x)) 5; g (x) = 3-5х ; f′ (x) = 5(3-5х)4 (-5) = -25 (3-5х)4 |
|
|
у = е3 - 2х у' = (е3 – 2x)' = e3 – 2x · (3 - 2х)' = -2e3 – 2x у = (0,3sinx) y' = ((0,3)sinx)'= (0,3)sinxln 0,3 · (sin x)' = (0,3)sinx ln 0,3 · cos x = ln 0,3cosx(0,3)sinx
у
=
у
= ln
(х2
+ 1)
y’
= (ln(x2+1))’
=
у = sin (3х + 5) у' = (sin(3x + 5))' = cos (3х + 5) · (3x· + 5)' = 3 cos(3x + 5); у = cos2x у' = (cos2 x)' = 2 cos x· (cos x)' = 2 cos x · (- sin x) = = -2 cos x sin x = - sin 2x; |
|
|
Застосування похідної до дослідження функцій та побудови графіків |
||||
|
Монотонність функції |
||||
|
Достатня умова зростання функції |
Достатня умова спадання функції |
Необхідна і достатня умова сталості функції |
||
|
Я f'(x)>0, то функція f(х) монотонно зростає на цьому інтервалі. |
Якщо в кожній точці інтервалу (а;b) f'(x)<0 , то функція f(х)
м |
Функція f(х) стала на інтервалі (а;b) тоді і тільки тоді, коли f(х)=0 в кожній точці цього інтервалу. |
||
|
Екстремуми функції |
||||
|
Необхідна умова екстремуму |
Достатня умова екстремуму |
|||
|
Я у = f(х), то ця точка є критичною точкою даної функції, тобто в цій точці похідна або дорівнює нулеві, або не існує.
xo — точка максимуму x1 — точка мінімуму |
Якщо функція у = f(х) неперервна в точці х0 і похідна f1(х) змінює знак в цій точці, то х0 - це точка екстремумa функції y=f(x) |
|||
|
Якщо f'(x)>0 при х < хо,
то х0 - точка максимуму
f'(x) змінює знак з «+» на «–» х0 – max |
Якщо f'(x)<0 при х < x0 f'(x)>0 при х > хо,
f'(x) змінює знак з «–»на «+» х0 - min |
|||
|
Найбільше і найменше значення функції, неперервній на відрізку |
||||
|
Функція, яка неперервна на відрізку, має на ньому найбільше і найменше значення або в критичних точках, або на його кінцях [а;b] |
||||
|
maxf(x)=f(x1) [a;b] minf(x)=f(x2) [a;b]
|
maxf(x)= f(a) [a;b] minf(x)= f(x1) [a;b]
|
maxf(x)=f(a) [a;b] minf(x)=f(b) [a;b]
|
||
|
Схема застосування похідної для знаходження інтервалів монотонності та екстремумів функції |
Схема знаходження найбільшого та найменшого значень функції, неперервній на відрізку |
||||||||||||||||||||||||||||||||||||||||
|
Етапи |
Приклад дослідження у = х3 - 3х2 |
Етапи |
Приклад
у
= х+ |
||||||||||||||||||||||||||||||||||||||
|
1. Знайти область визначення заданої функції |
D(y) = R |
1.Знайти похідну |
у’
=1 –
|
||||||||||||||||||||||||||||||||||||||
|
2. Знайти похідну |
у' = 3х2 - 6х |
2. Знайти критичні точки (f'(x)=0) |
x1= 6, х2 = -6- не входить до проміжку |
||||||||||||||||||||||||||||||||||||||
|
3. Знайти критичні точки (f'(x)=0) |
3х2 - 6х = 0, 3х(х - 2) = 0, х = 0 або х = 2. |
3. Знайти значення функції на кінцях проміжку(f(a) і f(b)) |
f(10) = 10 +3,6 = 13,6 |
||||||||||||||||||||||||||||||||||||||
|
4. В кожному з інтервалів, на які область визначення розби-вається критичними точками, визначити знак похідної і ха-рактер змінювання функції (за допомогою достатньої умови монотонності) |
y y'(1) = 3 · І2 – 6 - 1 = -3 < 0; у'(3) = 3 · 32 – 6 · 3 = 27 - 18 = 9 > 0. |
3. Знайти значення функції в тих критичних точках, які належать інтервалу [а; b] |
f(6) = 6 +6 = 12 |
||||||||||||||||||||||||||||||||||||||
|
5. Відносно кожної критичної точки визначити, чи є вона точкою екстремуму |
хmax = 0. хmin = 2. |
4. Із знайдених зна-чень вибрати найбіль-ше і найменше. |
Відповідь: fнайб. = f(12) =13,6; fнайм. = f(6) = 12. |
||||||||||||||||||||||||||||||||||||||
|
6. Записати результати дослідження |
у(х)
х(- у(х) (0; 2); хmax = 0; хmin = 2. |
|
|
||||||||||||||||||||||||||||||||||||||
|
Правила знаходження найбільшого і найменшого значення функції при розв'язуванні прикладних задач. |
|||||||||||||||||||||||||||||||||||||||||
|
1) «Перевести» задачу на мову функцій. Для цього вибирають х, через який виражають як функцію у = f(x) величину, яка потрібна
|
Число 20 запишіть у вигляді суми двох невід'ємних доданків так, щоб добуток їхніх квадратів був найбільшим. Розв'язання Нехай 1 доданок- х, тоді 2 доданок –( 20 – х), причому х є [0; 20]. Отже, задача зводиться до знаходження такого х, при якому функція f(x) = (20 - х)2 · х2 набуває найбільшого значення на відрізку [0; 20]. f'(x) = 2(20 - х) · (20 - х)' х2 + (20 - х)2 · 2х = 2х(20 - х)(20 – 2х). х1=0 : f(0) = 0; х2=20: f(l0) = 10 000; х3=10 : f(20) = 0. Отже, fнайб. = f(10) = 10 000. Відповідь: 20 = 10 + 10. |
||||||||||||||||||||||||||||||||||||||||
|
2) Знайти найбільше чи найменше значення цієї функції на деякому проміжку; |
|||||||||||||||||||||||||||||||||||||||||
|
3) З'ясувати, який практичний зміст (у межах даної задачі) має отриманий (на мові функцій) результат.
|
|||||||||||||||||||||||||||||||||||||||||
|
Схема дослідження функції |
|||||||||||||||||||||||||||||||||||||||||
|
Етапи |
Дослідіть функцію f(x) = х3 - 3х2 і побудуйте її графік. |
||||||||||||||||||||||||||||||||||||||||
|
1. Знаходимо область визначення функції. |
D(f)= R. |
||||||||||||||||||||||||||||||||||||||||
|
2. З'ясовуємо парність функції: Функція парна, якщо f (-х)= f (х) (графік симетричний відносно осі у). Функція парна, якщо f (-х) = -f (х) (графік симетричний відносно початку координат) |
f(-x) = (-x)3 - 3(-х)2 = -x3 - 3х2, то функція не є парною, не є непарною, отже не буде симетричною |
||||||||||||||||||||||||||||||||||||||||
|
3. Знаходимо точки перетину графіка з координатними осями:
|
Знайдемо абсциси точок перетину графіка з віссю Ох: x3 - 3х2 = 0; х2(х - 3) = 0; х = 0 або х = 3. Знайдемо ординату точки перетину графіка з віссю Οу: у = 03 - 3 · 02 = 0. |
||||||||||||||||||||||||||||||||||||||||
|
4. Визначити проміжки знакосталості: проміжки, на яких y>0 (графік вище осі Ох) проміжки, на яких y<0(графік нище осі Ох) |
f(x)
>0
х(3;
f(x)
<0
х(-
|
||||||||||||||||||||||||||||||||||||||||
|
5. Знайти похідну та критичні точки (f'(x)=0) |
f'(x) = 3х2 – 6х = 3х(х - 2). f'(x) = 0; 3х(x - 2) = 0; х = 0 або х = 2.
|
||||||||||||||||||||||||||||||||||||||||
|
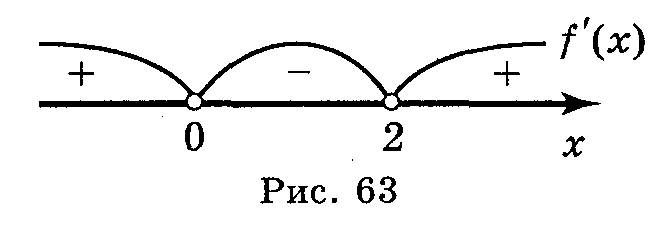
6. Визначити проміжки зростання, спадання та точки екстремуму функції (див схему). |
|
||||||||||||||||||||||||||||||||||||||||
|
7. Знайти значення функції в точках екстремуму |
f(0) = 0; f(2) = -4; |
||||||||||||||||||||||||||||||||||||||||
|
x
(-
0
(0; 2)
2
(2;
+
f'(x)
+
0
-
0
+
f(x)
0
-4
max
min
|
||||||||||||||||||||||||||||||||||||||||
|
Первісна, її властивості |
|
||||||||||||||||||||||||||||||||||||||||
|
Означення |
Функція F називається первісною для функції f на заданому проміжку, якщо для всіх х з цього проміжку F'(x)= f(x) |
|
|||||||||||||||||||||||||||||||||||||||
|
Основна властивість первісних |
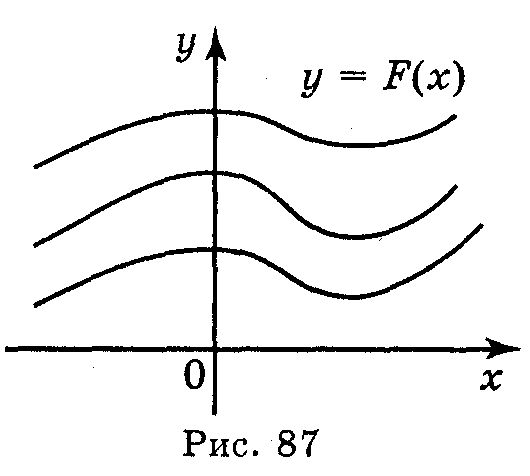
Т Теорема 2. Нехай функція F(x) є первісною для f(x) на деякому проміжку. Тоді будь-яка первісна для функції f(x) на цьому проміжку може бути записана у вигляді F(x) + С, де С — деяка стала (число). Теореми 1 і 2 виражають основну властивість первісної. Геометричного зміст: графіки будь-яких двох первісних для функції f одержуються один із одного паралельним перенесенням вздовж осі Οу. |
|
|||||||||||||||||||||||||||||||||||||||
|
Правила знаходження первісних |
1. Якщо F(x) і G(x) — первісні відповідно функцій f(x) і g(x) на деякому проміжку, то функція F(x) ± G(x) є первісною функції f(x) ± g(x). (F(x)± G(x))'=F'(x)± G(x)=f(x)± g(x) 2. Якщо F(x) є первісною для функції f(x), a C — стала, то CF(x) — первісна для функції Cf(x). F(x) = f(x) то (CF(x))' = CF'(x) = Cf(x)
3.
Якщо F(x)
є первісною для f(x),
a
k
і b
- постійні
числа, k
|
|
|||||||||||||||||||||||||||||||||||||||
|
Таблиця первісних |
|
||||||||||||||||||||||||||||||||||||||||
|
f(x) |
k- стала |
0 |
1 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
F(x) |
|
C |
x+c |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
f(x) |
|
|
ax+b |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
F(x) |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
Приклади знаходження первісних |
Самостійне опрацювання |
|
|||||||||||||||||||||||||||||||||||||||
|
1. Знайдіть всі первісні для функції
f(x)
= 5
F(x)
= 5х + С;
f(x)
=
х5
F(x)
=
Для даної функції f(x)=3х2-2х знайдіть первісну, графік якої проходить через точку А(1;4): F(x) = х3-х2+ С; F(1) =4; 1-1+С = 4; С=4, тобто F(x) = х3-х2+4 |
1. Знайдіть первісні для функції
а)
f(x)
=
2. Знайдіть первісну, графік якої проходить через задану точку А: а) f(x) = х4; А(-1; 0); б) f(x) = sinx, Α(π; 2). |
|
|||||||||||||||||||||||||||||||||||||||
|
Визначений інтеграл. Формула Ньютона-Лейбніца |
|
||||||||||||||||||||||||||||||||||||||||
|
К Теорема: Якщо f(x) неперервна і невід’ємна на відрізку [а; b] функція, а F(x) –її первісна на цьому відрізку, то площа відповідної криволінійної трапеції дорівнює: S = F(b)- F(a) Розглянемо неперервну функцію у = f(x), невід'ємну на відрізку [а; b].
Розіб'ємо
відрізок [а;
b]
на n
рівних частин а
= x0
<
x1
<
x2
< … <
xn-1
< хn
= b, довжина
кожної частини дорівнює
Утворимо суму S добутків f(xi)·Δx, де і = 0; 1; ... ; n - 1, яка називається інтегральною сумою:
S
За
означенням цю границю називають
інтегралом
функції
y
= f(x)
від
a
до b
і позначають
Число а називається нижньою межею інтегрування, а число b — верхньою межею інтегрування.
|
|
||||||||||||||||||||||||||||||||||||||||
|
Властивості інтеграла |
Приклади знаходження інтегралів |
|
|||||||||||||||||||||||||||||||||||||||
|
|
1)
2)
3)
4)
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
Застосування інтеграла |
|||||||||||||||||||||||||||||||||||||||||
|
Площа криволінійної трапеції |
Обчислення площ фігур |
||||||||||||||||||||||||||||||||||||||||
|
S=
|
S= |
S=
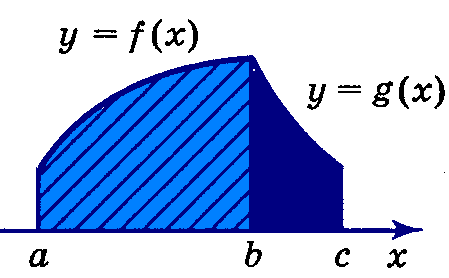
- |
S= |
S= |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||

 – довільна точка, що лежить у деякому
околі фіксованої точки х0.
– довільна точка, що лежить у деякому
околі фіксованої точки х0.
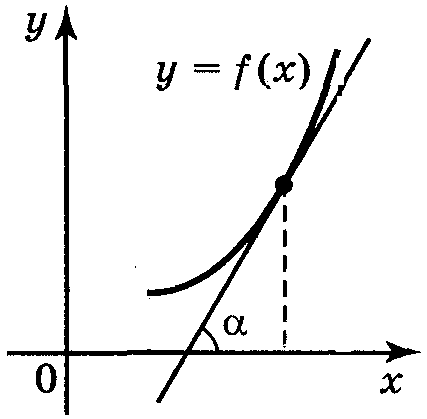
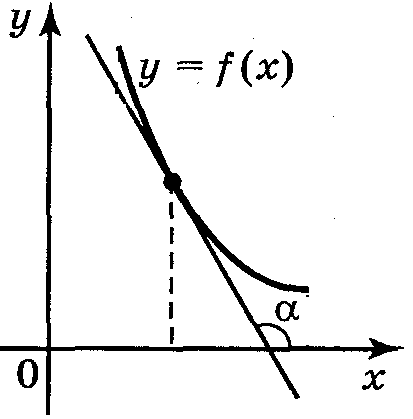 охідна
в точці х0
дорівнює кутовому коефіцієнту
дотичної до графіка функції
охідна
в точці х0
дорівнює кутовому коефіцієнту
дотичної до графіка функції
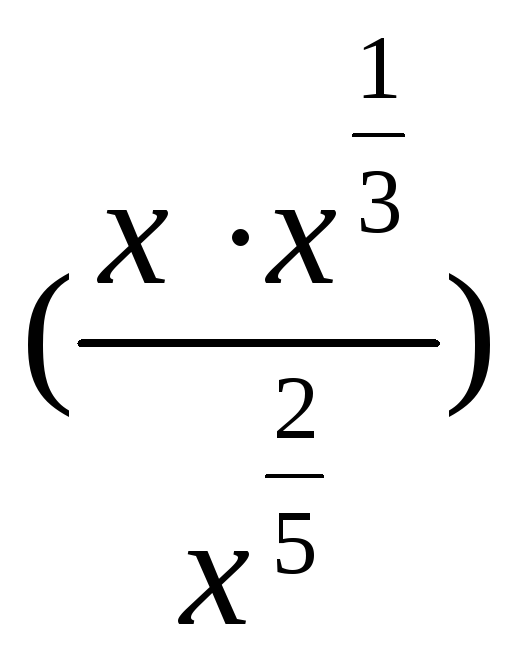 ′
=(
′
=(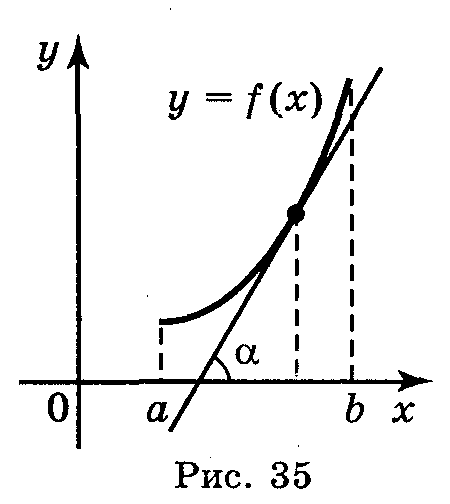 кщо
в кожній точці інтервалу (а;b)
кщо
в кожній точці інтервалу (а;b)
 онотонно
спадає
на цьому інтервалі.
онотонно
спадає
на цьому інтервалі.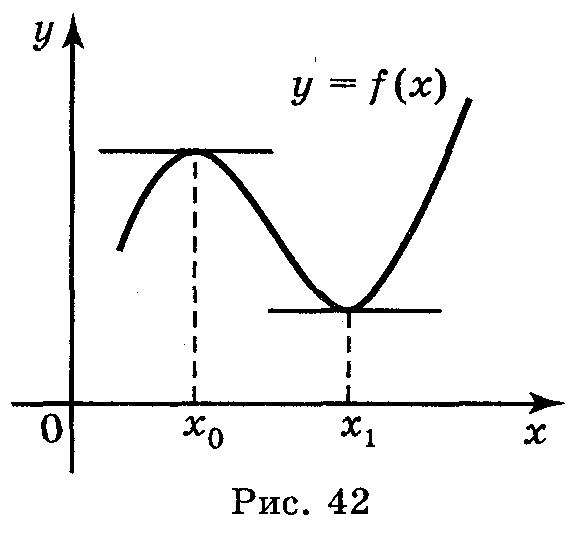 кщо
точка х0
- точка екстремуму функції
кщо
точка х0
- точка екстремуму функції
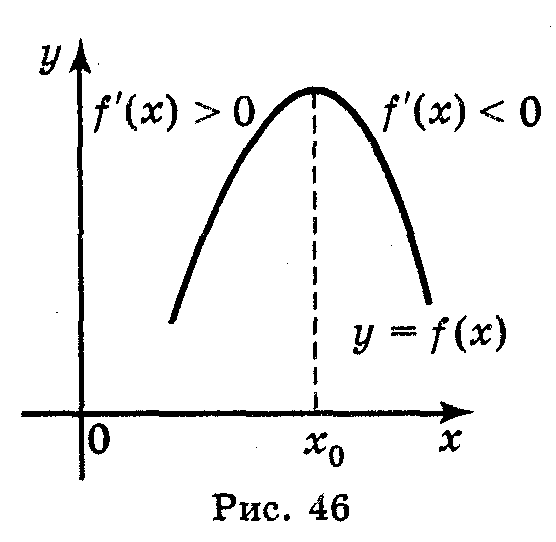 f'(x)
<0 при х > х0,
f'(x)
<0 при х > х0,
 то
х0
- точка мінімуму
то
х0
- точка мінімуму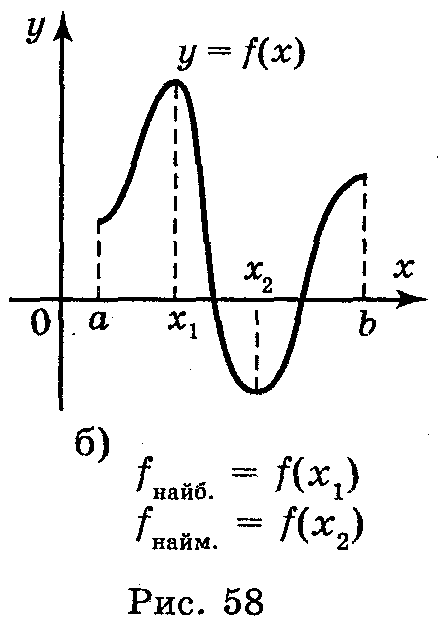
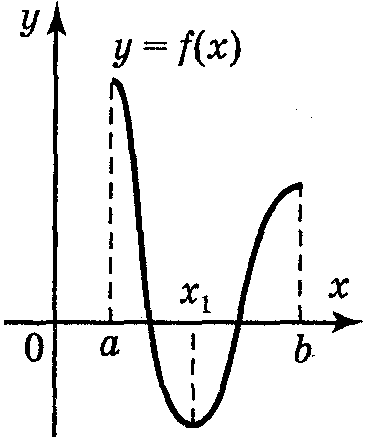
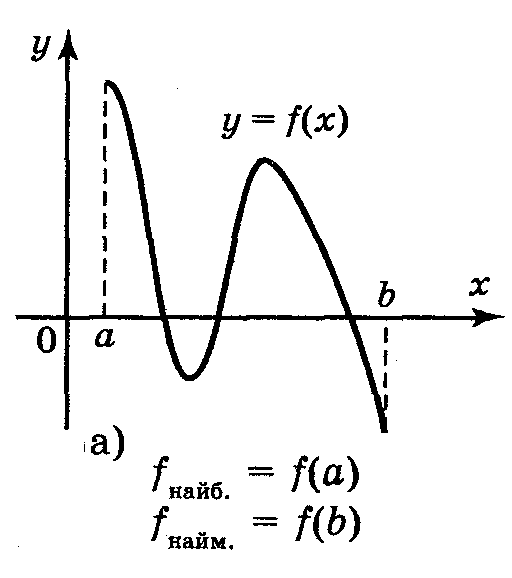
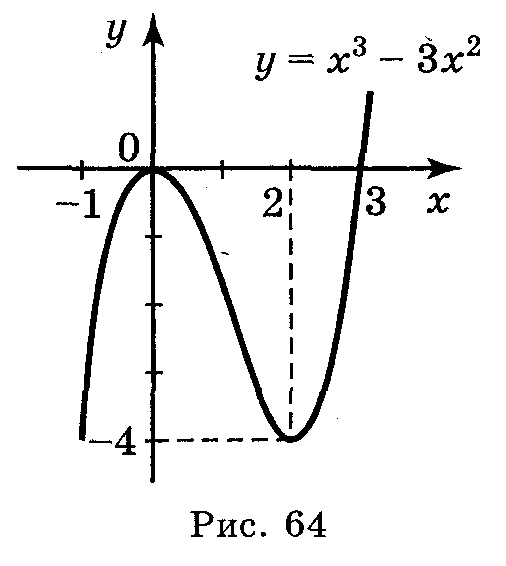
 еорема
1.
Нехай функція F(x)
є первісною для f(х)
на деякому проміжку. Тоді для довільної
постійної С функція F(x)
+ С
також є первісною для функції f(х).
еорема
1.
Нехай функція F(x)
є первісною для f(х)
на деякому проміжку. Тоді для довільної
постійної С функція F(x)
+ С
також є первісною для функції f(х). риволінійною
трапецією
називається фігура, обмежена графіком
неперервної функції у
= f(x),
яка не змінює знак на відрізку [а;
b],
прямими x
= а,
х
= b
і відрізком [а;
b].
риволінійною
трапецією
називається фігура, обмежена графіком
неперервної функції у
= f(x),
яка не змінює знак на відрізку [а;
b],
прямими x
= а,
х
= b
і відрізком [а;
b].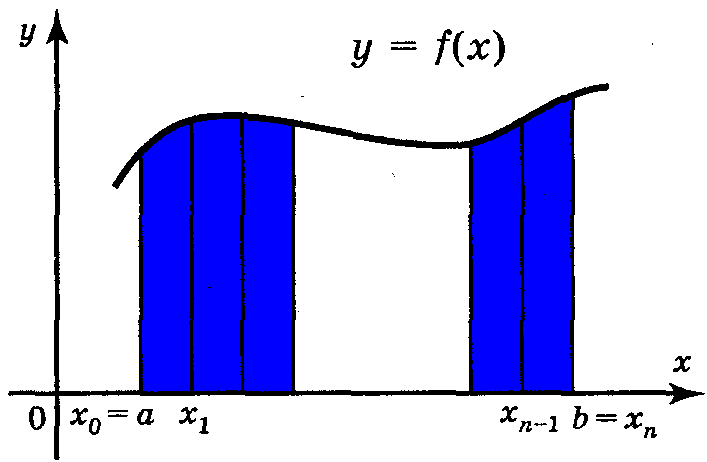 n
= f(xo)·Δx
+ f(x1)·Δx
+ f(x2)·Δx
+ ... + f(xn-1)·δx·.
Знайдемо
S =
n
= f(xo)·Δx
+ f(x1)·Δx
+ f(x2)·Δx
+ ... + f(xn-1)·δx·.
Знайдемо
S =
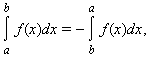
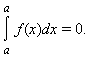
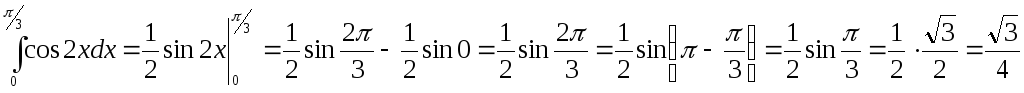 .
.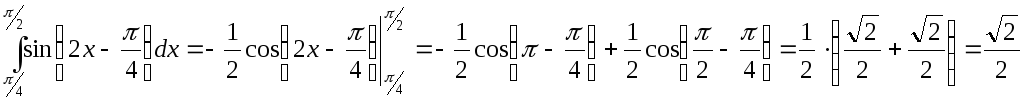 .
.