
алгебра функції
.doc|
|
Числові функції. Основні властивості функцій |
|
||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
Числовою функцією називається відповідність, яка кожному числу х деякої заданої множини зіставляє єдине число у.
П – незалежна змінна (аргумент функції), у – залежна змінна (функція). Множина значень х називається областю визначення функції (позначається D). Множина значень у називається областю значень функції (позначається Е). Графіком функції називається множина точок площини з координатами (х, f(х)). |
|
||||||||||||||
|
|
Основні властивості функції |
|
||||||||||||||
|
|
Парність функції |
Непарність функції |
Монотонність функції |
|
||||||||||||
|
|
Зростання |
Спадання |
|
|||||||||||||
|
|
Ф f (-х) = f (х)
Графік симетричний відносно осі у. |
Ф f (-х) = -f (х) Графік симетричний відносно початку координат |
Функція у = f(х) називається зростаючою на інтервалі (а;b), якщо для будь-яких х1 і х2 з інтервалу таких, що х1 х2 справедлива нерівність
f |
Функція у = f(х) називається спадаючою на інтервалі (а;b), якщо для будь-яких х1 і х2 з інтервалу таких, що х1 х2 справедлива нерівність
f
|
|
|||||||||||
|
|
Приклади графіків, які не є парними та непарними |
|
||||||||||||||
|
|
Періодичність функції |
Проміжки знакосталості функції |
Нули функции |
|
||||||||||||
|
|
Функція у = f(x) називається періодичною з періодом Т0, якщо для будь-якого х із області визначення числа х + Т і х – Т також належать області визначення і виконується рівність f (х) = f (х+Т) = f (х - Т)
Т
Т
Графік періодичної функції складається з необмежено повторюваних фрагментів. Щоб побудувати графік періодичної функції, будують фрагмент графіка на будь-якому відрізку довжиною Т (наприклад, [0; Т]), а потім роблять послідовні паралельні переноси фрагменту графіка на Т, 2Т, 3Т тощо, вздовж оси х (вправо і вліво). |
Проміжки, на яких y>0 х (-;-1)(0;1) |
Проміжки, на яких y<0 х (-1;0)(1; ) |
Нулем функції у = f(х) називається таке значення аргументу х0 , при якому функція обертається у нуль: f(х0) = 0 В нулі функції її гафік перетинає вісь Ох.
x=-2, x=0, x=2 – нулі функції |
|
|||||||||||
|
|
|
|
||||||||||||||
|
|
Геометричні перетворення графіків |
|||||||||||||||
|
|
Функція виду |
f(x) –f(x) |
f(x) f(–x) |
f(x) | f(x)| |
f(x) f(|x|) |
|||||||||||
|
|
Перет- ворення |
Симетрія відносно осі ОХ (точки перетину з Ох не змінюються) |
Симетрія відносно осі OY (точки перетину з Оу не змінюються) |
Частина графіка у верхній півплощині і на осі абсцис без змін, а замість частини графіка в нижній півплощині будуємо симетричну їй відносно осі OX |
Частину графіка для x ≥ 0 симетрично відображаємо відносно осі OY
|
|||||||||||
|
|
Приклад |
|
|
|
|
|||||||||||
|
|
Функція виду |
f(x) k f(x) |
f(x) f(kх) |
f(x) f(x) + b |
f(x) f(x + а) |
|||||||||||
|
|
Перетворення |
При k > 1 розтяг від точки (0; 0) вздовж осі Ox в k раз; при 0 < k < 1 стиск до точки (0;0) вздовж осі Oy в 1/k раз (точки перетину з Ох не змінюються) |
При k > 1 стиск до точки (0; 0) вдовж осі Ox в k раз; при 0<k < 1 розтяг від точки (0; 0) вздовж осі Oy в 1/k раз (точки перетину з Оу не змінюються) |
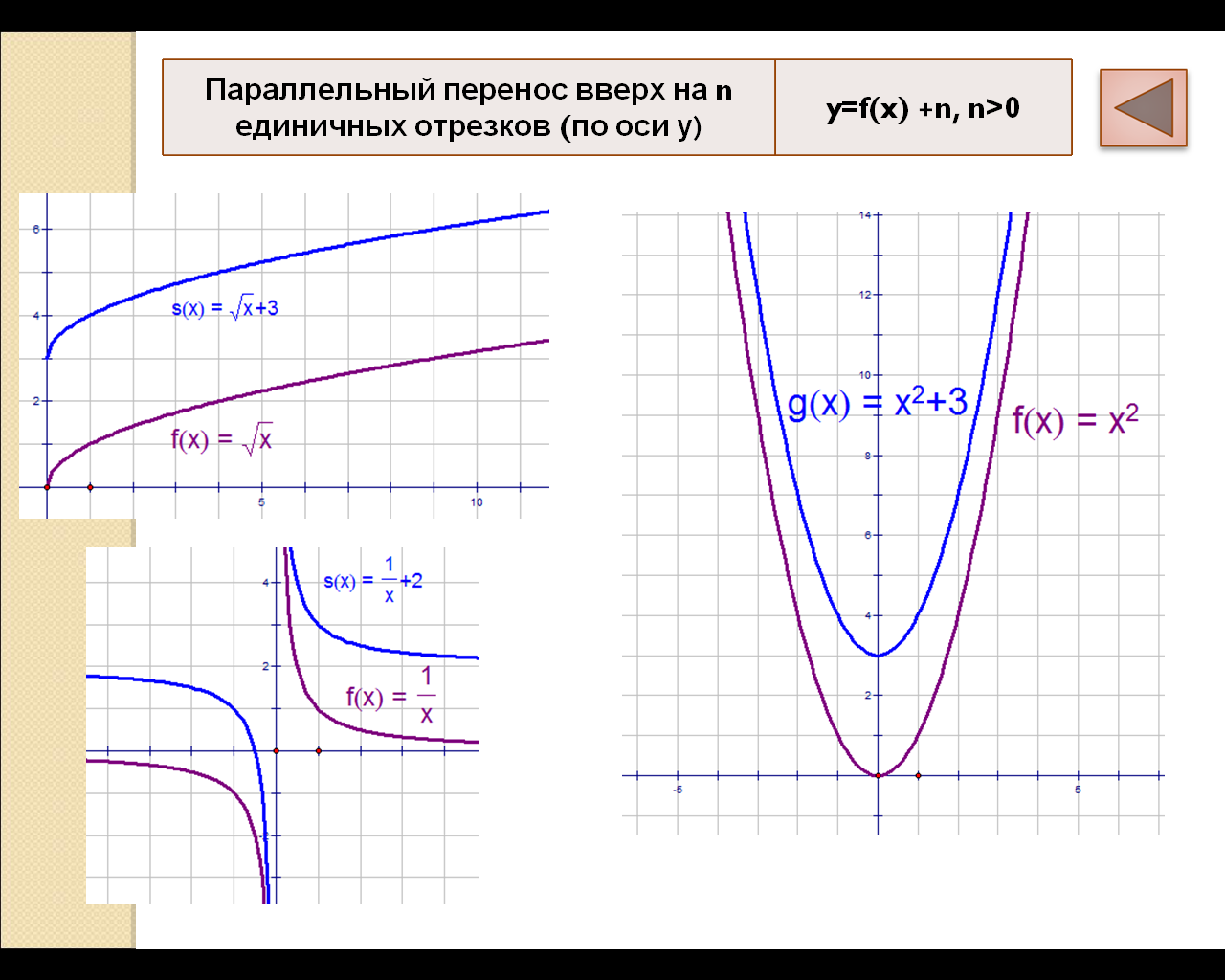
Паралельне перенесення вдовж осі OY на b одиниць |
Паралельне перенесення вдовж осі ОХ на (-а) одиниць
|
|||||||||||
|
Приклад |
|
|
|
|
|
|||||||||||
|
Геометричні перетворення графіків |
||||
|
|
Масштабування |
Симетричність |
Паралельне перенесення |
Відображення |
|
Перетворення пов’язані з аргументом функції |
f(x) f(kх) |
f(x) f(–x) |
f(x) f(x + а) |
f(x) f(|x|) |
|
Дії над базовим графіком |
- при k > 1 стиск до точки (0; 0) вдовж осі Ox в k раз; - при 0<k< 1 розтяг від точки (0; 0) вздовж осі Ox в 1/k раз (точки перетину з Оy не змінюються) |
симетрія відносно осі OY (точки перетину з Оу не змінюються) |
паралельне перенесення вдовж осі ОХ на (-а) одиниць
|
частину графіка для x ≥ 0 симетрично відображаємо відносно осі OY
|
|
Приклад |
|
|
|
|
|
Перетворення пов’язані з аргументом функції |
f(x) k f(x) |
f(x) –f(x) |
f(x) f(x) + b |
f(x) |f(x)| |
|
Дії над базовим графіком |
- при k > 1 розтяг від точки (0; 0) вздовж осі Oy в k раз; - при 0 < k < 1 стиск до точки (0;0) вздовж осі Oy в 1/k раз (точки перетину з Ох не змінюються) |
симетрія відносно осі ОХ (точки перетину з Ох не змінюються) |
паралельне перенесення вдовж осі OY на b одиниць |
частина графіка у верхній півплощині і на осі абсцис без змін, а замість частини графіка в нижній півплощині будуємо симетричну їй відносно осі OX |
|
Приклад |
|
|
|
|
|
Корінь n-го степеня, його властивості |
|||||||||||||||
|
Арифметичним коренем n-ої степені з додатнього числа а називається таке додатнє число b, n-а степінь якого дорівнює а, тобто
|
Функції
у
=
|
||||||||||||||
|
Властивості коренів |
Приклади графіків |
||||||||||||||
|
|
Приклади |
Самостійне розв’язання |
n - непарне |
n - парне |
|||||||||||
|
|
|
|
|
|||||||||||
|
2.
|
|
|
|||||||||||||
|
3.
|
|
|
|||||||||||||
|
4.
( |
( |
|
|||||||||||||
|
5.
|
|
|
|||||||||||||
|
6.
(
|
|
Властивості функції |
|||||||||||||
|
Область визначення: |
|||||||||||||||
|
R |
∞ |
||||||||||||||
|
7.
|
Область значень: |
||||||||||||||
|
R |
∞ |
||||||||||||||
|
Парність функції: |
|||||||||||||||
|
8.
Якщо а
> b
Наслідки:
1)
Якщо а
> 1, то
2) Якщо 0 < а < 1,
то
0 <
3)
а
> b
|
1.
Порівняти числа
32
> 27, тоді
2.
Розташувати в порядку зростання:
|
1. Порівняйте числа:
а)
б)
в)
2. Розташуйте в порядку зростання
a)
б)
|
функція непарна |
функція не є ні парної, ні непарною. |
|||||||||||
|
Нулі: у = 0 при х = 0 |
|||||||||||||||
|
Проміжки знакосталості: |
|||||||||||||||
|
y>0 х(-;0) y<0 х(0;) |
y>0 х(0;) |
||||||||||||||
|
Проміжки монотонності: функція зростає для всіх х з області визначення |
|||||||||||||||
|
Графіки функцій проходять через точки: |
|||||||||||||||
|
(-1; 1), (0;0), (1;1) |
(0;0), (1;1) |
||||||||||||||
|
Степені з раціональним показником, їхні властивості |
|||||||||||||||
|
Степенем
числа а>0 з раціональним показником,
ar
= |
|||||||||||||||
|
Властивості степенів |
Приклади |
Самостійне розв'язання |
|||||||||||||
|
Для будь-яких раціональних чисел r і s та будь-яких а>0 і b>0: |
|||||||||||||||
|
1. ar as = ar+s |
1)
2)
3)
4) 5) Порівняйте числа:
а)
б) 2300 і 3200 : 2300 = (23)100 = 8100; 3200 = (32)100 = 9100 8<9, тоді маємо: 8100 <9100, тобто 2300<3200 |
Подайте у вигляді кореня вираз а)31,2 ;б)41,25 Подайте у вигляді степеня:
а)
Знайдіть значення виразу:
Розкладіть на множники:
Порівняйте числа:
а)
|
|||||||||||||
|
2. ar : as = ar-s |
|||||||||||||||
|
3. (ar)s = ars |
|||||||||||||||
|
4. (ab)r = ar br |
|||||||||||||||
|
5.
|
|||||||||||||||
|
6.
а0
= 1, а
≠
0,
n
|
|||||||||||||||
|
7.
а-n
=
|
|||||||||||||||
|
8. Якщо 0< а< b,тоді аг< bг, при r >0, аг>bг, аг> bг, при r <0 |
|||||||||||||||
|
9. Якщо r > s, тоді аг>аs, якщо а>1 аг<аs, якщо 0<а<1 |
|||||||||||||||
|
Ірраціональні рівняння |
|||||||||||||||
|
Для того, щоб розв'язати ірраціональне рівняння його приводять до рівнопотужньої системи, яка містить рівняння та нерівність. |
Приклади |
Самостійне розв’язання |
|||||||||||||
|
1.
якщо а>0, рівняння рівносильне рівнянню f(х) = а2 |
Відповідь: х=24 |
|
|||||||||||||
|
2.
|
7-х=(х-1)2; х=-2; х=3 Відповідь: х=3 |
|
|||||||||||||
|
3 |
3-х=х2-5х-2; х=-1; х=5 Відповідь: х=-1 |
|
|||||||||||||
|
Показникова та логарифмічна функції, їх властивості та графіки |
|
||||||||||||||
|
|
Властивості
|
Показникова функція |
Логарифмічна функція |
|
|||||||||||
|
Функція виду у = ах, де а — задане число, а > 0, називається показниковою функцією |
Функція виду у = loga x, де а — задане число, а > 0, а ≠ 1 називається логарифмічною функцією |
|
|||||||||||||
|
a>1 |
0<a<1 |
a>1 |
0<a<1 |
|
|||||||||||
|
1 |
D (у) |
R |
R |
(0;+) |
(0;+) |
|
|||||||||
|
2 |
Е(у) |
(0;+) |
(0;+) |
R |
R |
|
|||||||||
|
3 |
Парність |
ні парна, ні непарна |
ні парна, ні непарна |
ні парна, ні непарна |
ні парна, ні непарна |
|
|||||||||
|
4 |
Нулі функції |
х =0: у =1 |
х =0: у =1 |
у=0: х=1 |
у=0: х=1 |
|
|||||||||
|
5 |
Проміжки монотонності |
зростає на всій області визначення |
спадає на всій області визначення |
зростає на всій області визначення |
спадає на всій області визначення |
|
|||||||||
|
6 |
Проміжки, на яких у>0 |
якщо х < 0, то у < 1 якщо х > 0, то у > 1 |
якщо х < 0, то у > 1 якщо х > 0, то у < 1 |
loga x > 0, якщо х>1 |
loga x > 0, якщо 0<х<1 |
|
|||||||||
|
7 |
Проміжки, на яких у<0 |
немає |
немає |
loga x < 0, якщо 0<х<1 |
loga x < 0, якщо х>1 |
|
|||||||||
|
Графік
|
Графіком показникової функції є крива, яка називається експонентою. |
|
|
|
|||||||||||
|
|
|
|
|||||||||||||

 означення
: у = f(х),
де
х
означення
: у = f(х),
де
х
 ункція
називається парною,
якщо:
для будь-якого х
з області визначення
ункція
називається парною,
якщо:
для будь-якого х
з області визначення
 ункція
називається непарною,
якщо:
для будь-якого х
з області визначення
ункція
називається непарною,
якщо:
для будь-якого х
з області визначення
 (x1)
f (x2)
(x1)
f (x2) (x1)
f (x2)
(x1)
f (x2)

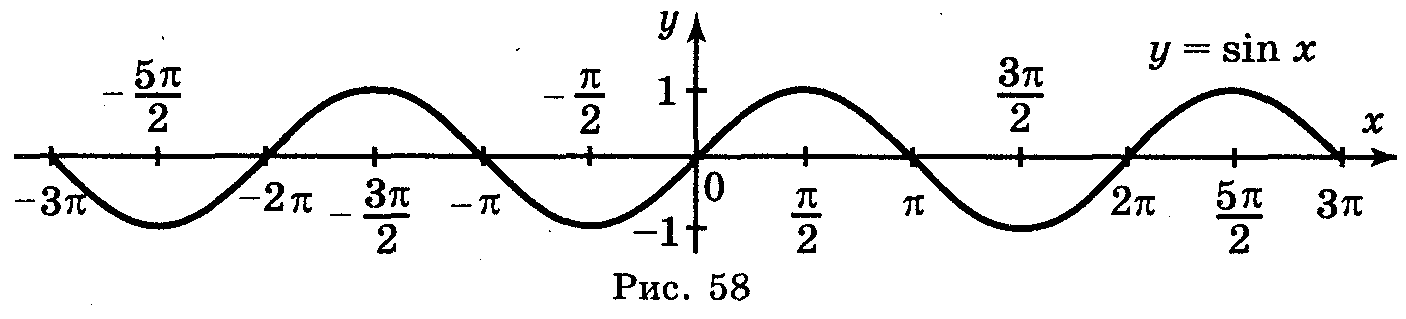




























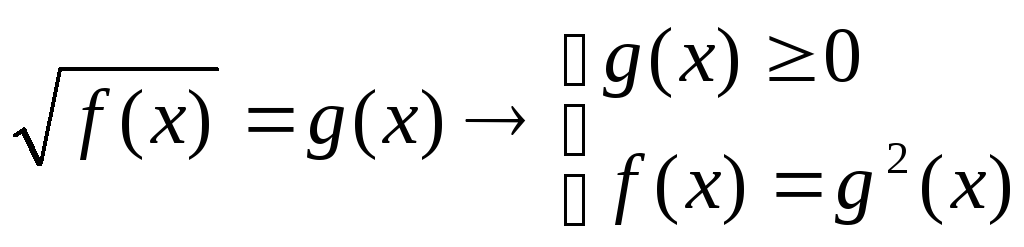 або
або

 або
або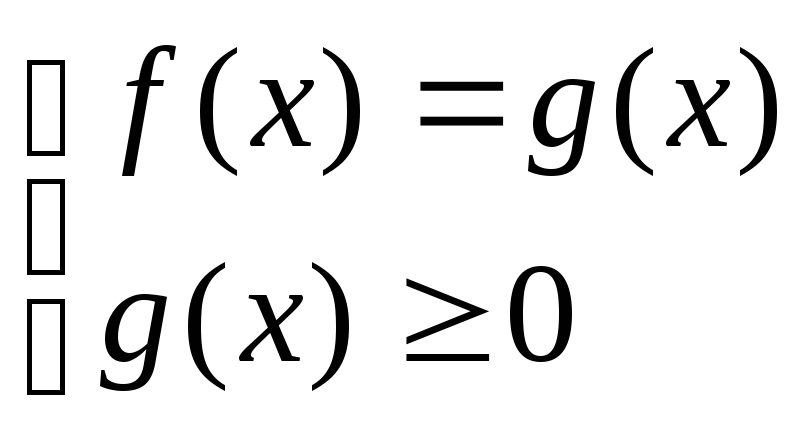 або
або



