
алгебра тригоном
.doc|
Властивості тригонометричних функцій |
|||||
|
|
Властивості
|
ФУНКЦІЯ |
|||
|
y=sinx |
y= cosx |
y =tgx |
y =ctgx |
||
|
1 |
D (у) |
R |
R |
x |
x |
|
2 |
Е(у) |
[-1;1] |
[-1;1] |
R |
R |
|
3 |
Парність |
Непарна sin(-x)=-sinx |
Парна cos(-x)= cosx |
Непарна tg(-x)=-tgx |
Непарна ctg(-x)=-ctgx |
|
4 |
Періодичність, період |
2 |
2 |
|
|
|
5 |
Нулі функції |
n, nZ |
|
n, nZ |
|
|
6 |
Якщо х =0 |
sinx=0 |
cosx=1 |
tgx=0 |
невизначено |
|
7 |
Проміжки, на яких у>0 |
(2n; +2n), nZ |
(- |
( |
( |
|
8 |
Проміжки, на яких у<0 |
(+2n; 2+2n), nZ |
( |
(- |
(- |
|
9 |
Проміжки зростання |
[ |
[-+2n], nZ
|
(- |
немає |
|
10 |
Проміжки спадання |
[ |
[2n; +2n], nZ |
немає |
(n, +n), nZ |
|
11 |
Найменші значення |
у=-1,
якщо х= |
у=-1,
якщо х= |
немає |
немає |
|
12 |
Найбільші значення |
у
y=sinx |
у=1,
якщо х= |
немає |
немає |
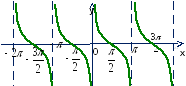
у=sinx
y=ctgx
y=tgx
y=cosx

|
Найпростіші тригонометричні рівняння |
|
||||||
|
sin x= a |
cos x = a |
tgx = a |
|
||||
Ці дві формули можна з’єднати в одну: x = (-1)narcsin a +n, nZ
Приклад
1.
sinx
=
х
=
(-1)n
arcsin
х
=
(-1)n
Приклад
2.
sin
х
= -
х
= (-1)n
arcsin
оскільки
arcsin
х
=(-1)n
·
х
= (-1)n+1
+ πп,
п
|
Ці дві формули можна з’єднати в одну: x = ±arccos a +2n, nZ
Приклад
1. cos
x
=
х
= ±
arccos
х
= ±
Приклад
2.
cos
x
= -
х
= ±arccos
arccos
x
= ±
|
x= arctga+n, nZ П
tg
x
=
х
=
arctg
х
=
Приклад 2.
tg
x
= -1
arctg
(-1) =
х
=
c
x= arcctga+n, nZ Приклад 1.
ctg
x
–
ctg
х
=
x
= arcсtg
x
=
Приклад 2. ctgx= -1, оскільки arcctg (-1) = π -arcctg 1 =
=
π
-
х
= |
|
||||
|
a = -1 sin x=-1
x=- |
a = 0 sin x=0 x=n, nZ |
a = 1 sin x=1
x= |
a = -1 cos x=-1 x=+2n, nZ |
a = 0 cos x=0
x= |
a = 1 cos x=1 x=2n, nZ |
|
|
|
|
|
||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
Обернені тригонометричні функції, їх властивості |
|||||
|
Арксинусом
числа
а
називається таке число із проміжку
Арккосинусом числа а називається таке число з проміжку [0; π], косинус якого дорівнює а.
Арктангенсом
числа а
називається таке число з проміжку
Арккотангенсом числа а називається таке число із інтервалу (0; π), котангенс якого дорівнює а.
|
|||||
|
|
Властивості
|
ФУНКЦІЯ |
|||
|
y=arcsinx |
y= arccosx |
y =arctgx |
y =arcctgx |
||
|
1 |
D (у) |
[-1;1] |
[-1;1] |
R |
R |
|
2 |
Е(у) |
[ |
[0;π] |
( |
(0;π) |
|
3 |
Парність |
непарна arcsin (-х) = -arcsin х |
ні парна, ні непарна arccos (-х) = π - arccos х |
непарна arctg (-х) = - arctg х |
ні парна, ні непарна arcctg (-х) = π - arcctg х |
|
4 |
Нулі функції |
у=0 при х=0 |
у=0 при х=1 |
у=0 при х=0 |
немає |
|
5 |
Проміжки, на яких у>0 |
х(0;1] |
х[-1;0) |
х(0;) |
хR |
|
6 |
Проміжки, на яких у<0 |
х[-1;0) |
немає |
х[-;0) |
немає |
|
7 |
Проміжки монотонності |
зростає на всій області визначення |
спадає на всій області визначення |
зростає на всій області визначення |
спадає на всій області визначення |
|
8 |
Асимптоти |
немає |
немає |
|
у=0; у=π |
|
|
Графік |
Г
|
Графік
функції у
=
arccos x
одержимо із графіка функції у
= cos x,
x
п |
Графік
функції у
= arctg х
одержимо із графіка функції у
= tg х,
х
перетворенням симетрії відносно прямої у = х
|
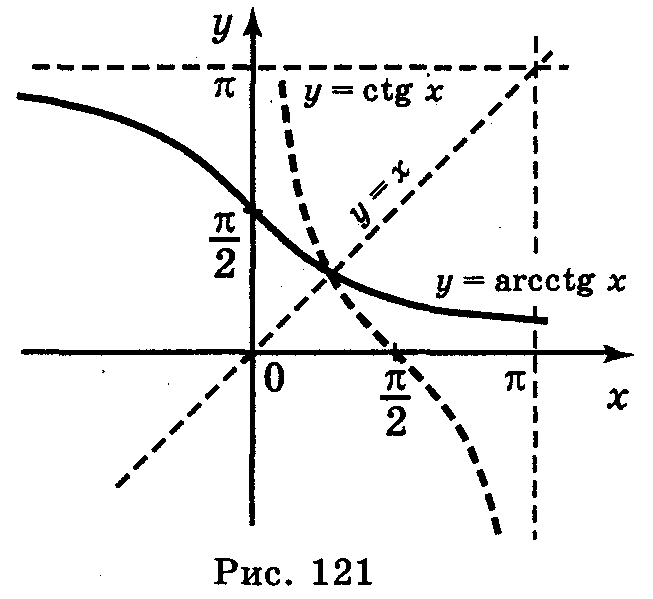
Графік функції у = arcctg x можна одержати із графіка функції у = ctg x у результаті перетворення симетрії відносно прямої у = х
|
|
Тригонометричні функції |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Тригонометричні функції довільного кута |
Радіана міра кутів і дуг |
Тригонометричні функції числового аргументу |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Градусом
називається
1º
= 60', 1' = 60'', 1' =
1 радіан — центральний кут, який опирається на дугу, довжина якої дорівнює радіусу кола. Залежність між радіанним і градусним вимірюванням кутів: 180° = π рад
n
– формула
переходу від градусної
міри кута в
радіанну
45°
= 45 ·
q
– формула
переходу від радіанної
міри
кута до градусної.
|
Синусом числа α називається ордината точки Рα, утвореної поворотом точки Рα (1; 0) навколо початку координат на кут в α радіан. (позначається sinα)
К (позначається cos α) Тангенсом числа α називається відношення синуса числа α до його косинуса. (позначається tgα) Котангенсом числа α називається відношення косинуса числа α до його синуса. (позначається ctgα) |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Знаки тригонометричних функцій |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
sin α |
cos α |
tg α , ctg α |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Таблиця значень синуса, косинуса, тангенса і котангенса деяких чисел |
Тригонометричне коло |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
α
0
π=180°
2π=360°
sin
α
0
1
0
-1
0
cos
α
1
0
-1
0
1
tg
α
0
1
-
0
-
0
ctg
α
-
1
0
-
0
- |
Приклад
застосування
cos
2250
= -
sin
2400
= -
cos
1200
= -
sin
1200
=
cos
1800
= -1
sin
900
=
1
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Основні формули тригонометрії |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Співвідношення між тригонометричними функціями одного аргументу |
Тригонометричні функції подвійного аргументу |
Вираз тригонометричних функцій через тангенс половинного кута |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
cos2+sin2=1 tgctg=1
|
sin2α = 2sinαcosα cos2α = cos2α – sin2α cos2α = 1-2 sin2 cos2α =2 cos2-1
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Формули тригонометричних функцій суми і різниці двох чисел |
Тригонометричні функції половинного аргументу |
Формули перетворення добутку у суму
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
sin(α + β) = sinαcosβ + cosαsinβ sin(α – β) = sinαcosβ – cosαsinβ cos(α – β) = cosαcosβ + sinαsinβ cos(α + β) = cosαcosβ – sinαsinβ
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Формули перетворення суми у добуток |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Щоб
записати тригонометричні функції
чисел виду
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||

 кщо
а>1,
коренів немає
кщо
а>1,
коренів немає
 кщо
а>1,
коренів немає
кщо
а>1,
коренів немає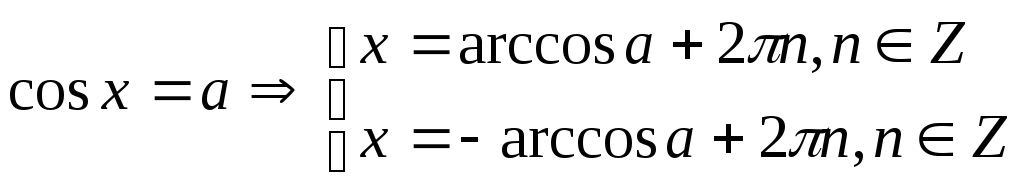
 риклад
1.
риклад
1.
 tgx
= a
tgx
= a рафік
функції у
=
arcsin х
одержимо
із графіка функції у
=
sin х,
х
рафік
функції у
=
arcsin х
одержимо
із графіка функції у
=
sin х,
х
 еретворенням
симетрії відносно прямої у = х
еретворенням
симетрії відносно прямої у = х

 осинусом
числа α
називається абсциса точки Рα,
утвореної поворотом точки Рα
(1; 0) навколо початку координат на кут
в α радіан.
осинусом
числа α
називається абсциса точки Рα,
утвореної поворотом точки Рα
(1; 0) навколо початку координат на кут
в α радіан.







