
- •Глава I. Общие сведения о дифференциальных уравнениях § 1. Дифференциальное уравнение и его решения. Основные понятия
- •Разбор типовых примеров
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •§3. Геометрическое истолкование дифференциального уравнения. Метод изоклин.
- •Задачи для самостоятельного решения
Разбор типовых примеров
Пример 1.Показать, что![]() ‑ решение уравнения
‑ решение уравнения![]() .
.
Решение:![]() ,
,
![]()
![]() ,
,
![]() .
.
Пример 2.Показать, что![]() ,
,
![]() ‑интегральная кривая уравнения
‑интегральная кривая уравнения![]() .
.
Решение: По условиюy = tx; y=
![]()
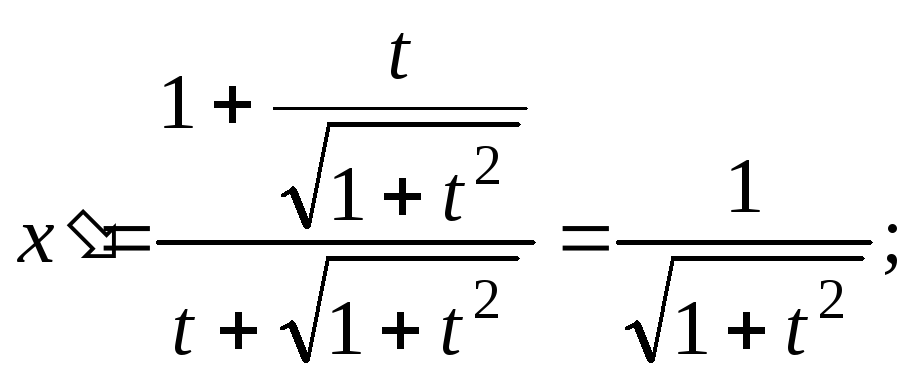
![]()
Подставляя вместо х, у, у их выражение черезtв левую часть данного уравнения с учетом, чтоу= tx, получим
![]()
Пример 3.Показать, что
![]() удовлетворяет уравнению
удовлетворяет уравнению![]() .
.
Решение:
![]() ,
,
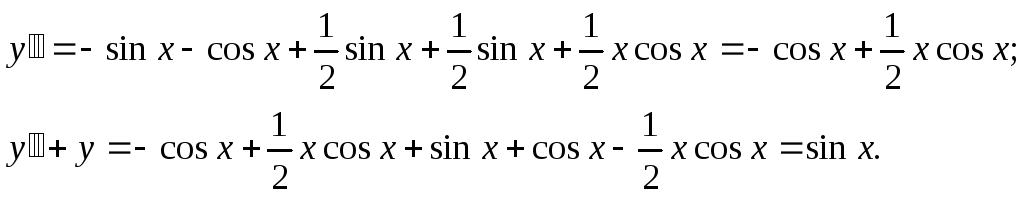
Пример 4. Показать, что![]() для любого фиксированногоС
R является интегралом дифференциального
уравнения
для любого фиксированногоС
R является интегралом дифференциального
уравнения![]() .
.
Решение:![]()
![]() (dC= 0, т.к. C= const)
(dC= 0, т.к. C= const) ![]() .
.
Пример 5.Показать, что дифференциальные уравнения
![]() ,
,
![]()
попарно неэквивалентны.
Решение: Согласно определению
достаточно показать, что множества
решений трех данных уравнений не
совпадают. В этом проще всего убедиться,
заметив, что первому уравнению
удовлетворяют функции![]() ,
,
![]() ,
второму ‑
,
второму ‑![]() ,но
не удовлетворяет
,но
не удовлетворяет ![]() ,
а третьему удовлетворяет
,
а третьему удовлетворяет![]() ,
но не удовлетворяет
,
но не удовлетворяет![]() .
.
6.Показать, что функция![]() является общим решением уравнения
у=
является общим решением уравнения
у=![]() ,
но не уравнения у=3у2.
,
но не уравнения у=3у2.
Решение.Из системы уравнений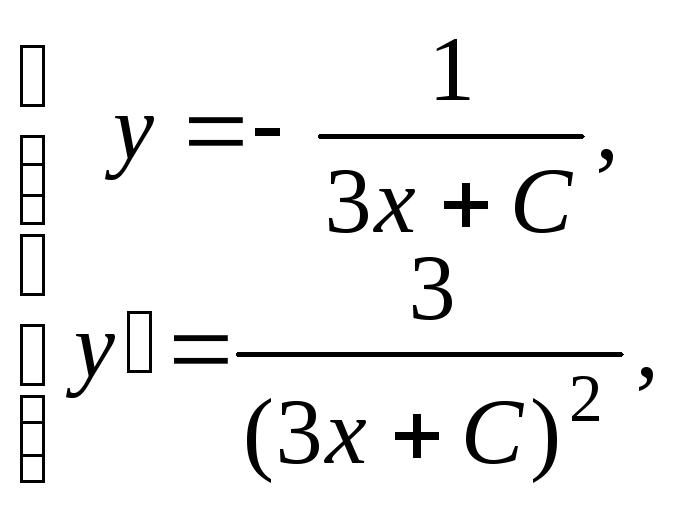 находимС=
находимС=![]()
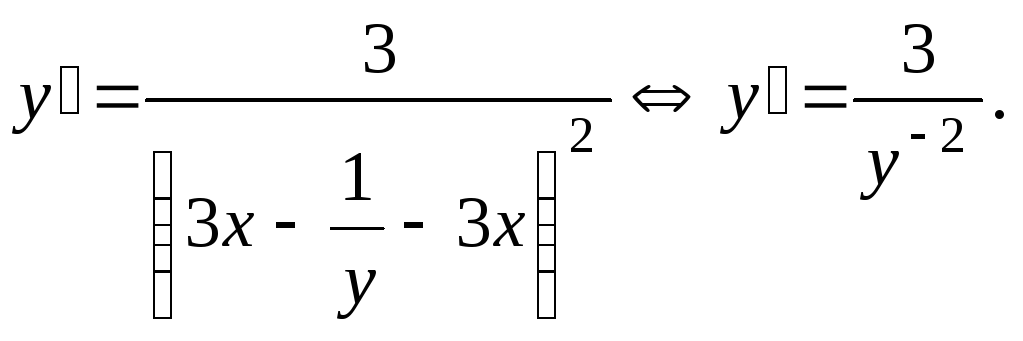
Следовательно,
![]() общее решение
уравнения
общее решение
уравнения
![]() ,правая часть которого не определена
при
,правая часть которого не определена
при![]() .Уравнение же
.Уравнение же![]() имеет частное решение
имеет частное решение![]() ,
не получаемое из
,
не получаемое из
![]() ни при каком значенииС.
ни при каком значенииС.
7.Показать, что уравнение![]() является общим интегралом уравнения
является общим интегралом уравнения
![]()
Решение:Обозначим![]() .
Тогда
.
Тогда ![]() ;
;
![]() ;
;![]()
8.Показать, что уравнениеу3=![]() является общим интегралом уравнения в
дифференциалах
является общим интегралом уравнения в
дифференциалах
![]()
Решение:
![]()
![]()
![]()
Отметим, что данное уравнение
![]() не является общим интегралом для
уравнения в дифференциалах
не является общим интегралом для
уравнения в дифференциалах![]() ,
так как последнее имеет дополнительное
частное решение
,
так как последнее имеет дополнительное
частное решение![]() .
.
9.Найти дифференциальное уравнение
для семейства кривых, заданного уравнением![]() .
.
Решение.![]() ,
,
![]()
![]() .
.
10.Найти дифференциальное уравнение
для семейства кривых![]() .
.
Решение.![]() .
.
Задачи для самостоятельного решения
В следующих задачах требуется показать, что данные функции являются решениями указанных дифференциальных уравнений и найти области определения этих решений:
1.
![]()
![]()
2.
![]()
![]() .
.
3.
![]()
![]()
![]()
4.
![]()
![]()
5.![]()
![]() .
.
6.
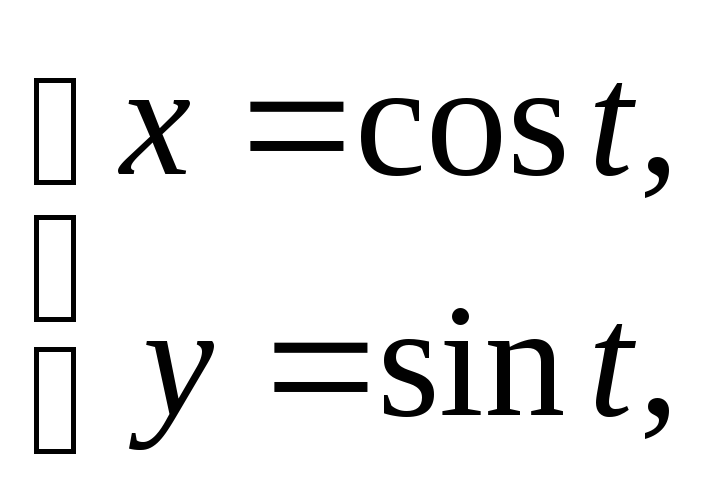
![]() .
.
7.
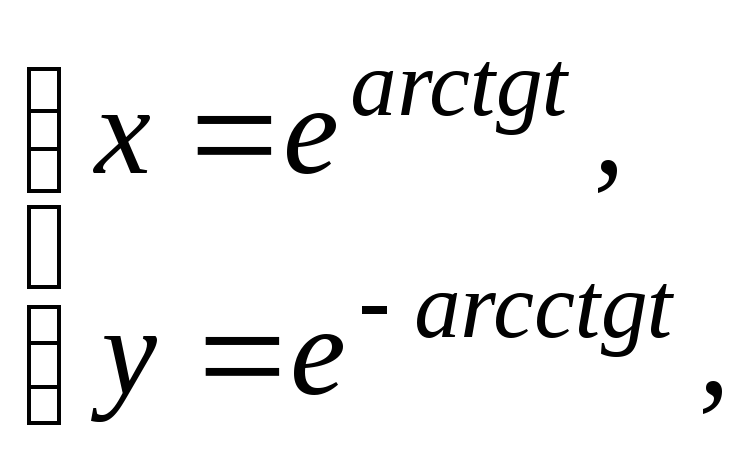
![]()
8.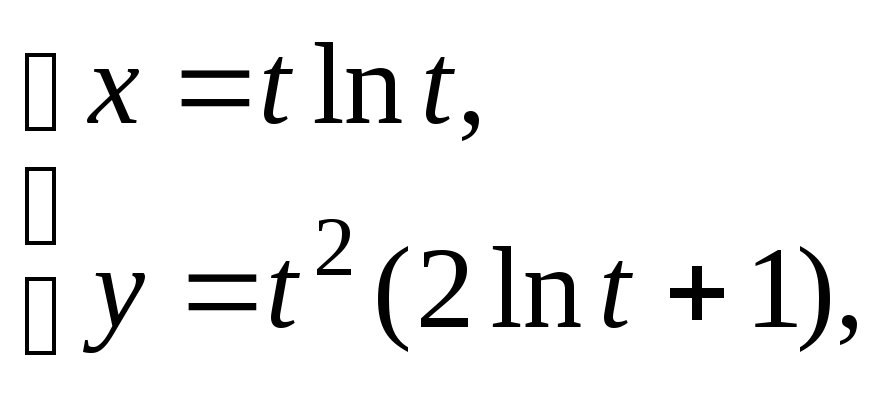
![]()
9.
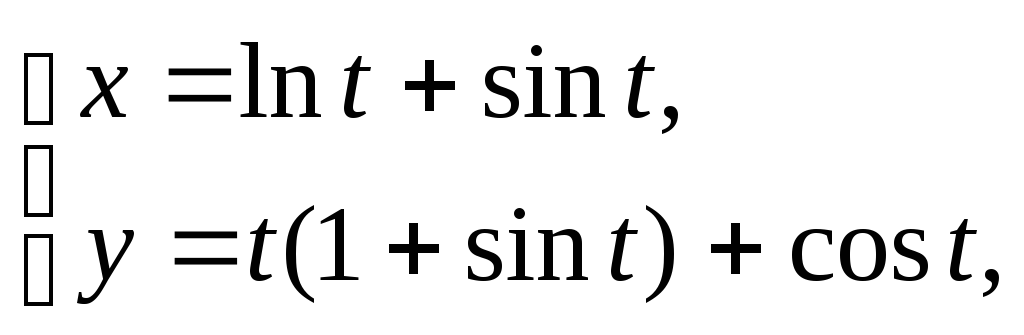
![]()
10.
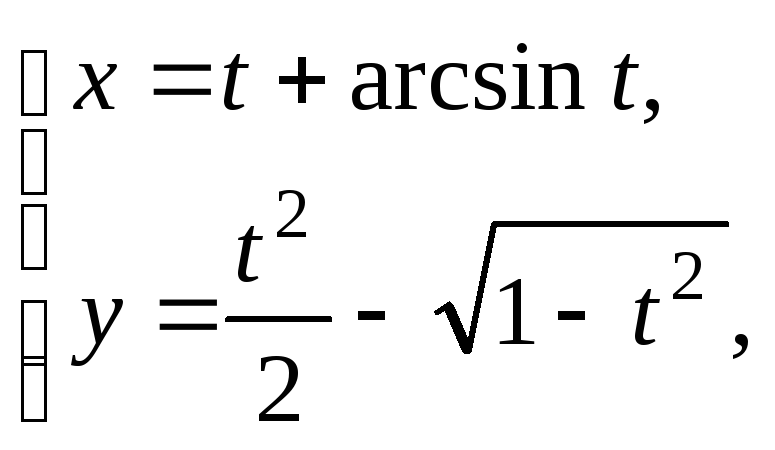
![]()
Проверить, являются ли данные функции и уравнения общими решениями и интегралами для указанных дифференциальных уравнений:
11.![]()
![]()
12.![]()
![]()
13.![]()
![]()
14.![]()
![]()
15.![]()
![]()
§2. Задачи на составление дифференциальных уравнений
Не существует каких-либо общих правил для составления дифференциальных уравнений по условиям конкретной задачи. Условия задачи должны быть таковы, чтобы позволяли составить соотношение, связывающее независимое переменное, функцию и ее производную (или производные). Если это задача геометрического характера, то наличие в ее данных касательной (или нормали) или некоторых связанных с ней отрезков дает возможность написать соотношение между координатами точек кривой и угловым коэффициентом касательной (задача 1, 4). В задачах физического или механического характера, в случае если задается скорость какого-нибудь процесса, бывает возможно сразу написать соответствующее дифференциальное уравнение (задача 2, 5). В других случаях, предварительно устанавливая соотношение между приращениями переменных, затем переходом к пределу получают дифференциальное уравнение (задача 3).
В качестве примеров рассмотрим несколько задач, приводящих к дифференциальным уравнениям.
Задача 1. Найти кривые, обладающие в каждой точке тем свойством, что отрезок касательной, заключенный между осями координат, делится в точке касания пополам.
Р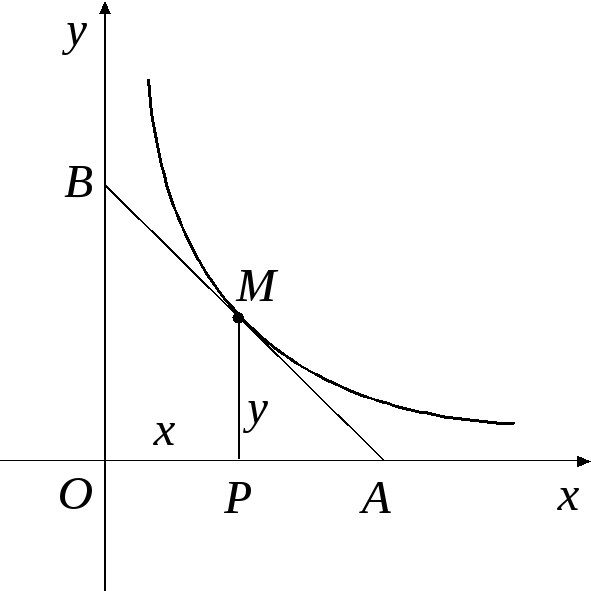 ешение.Пусть
ешение.Пусть![]() – произвольная точка кривой (см. рис.1),
обладающая требуемым свойством:
– произвольная точка кривой (см. рис.1),
обладающая требуемым свойством:![]() .
Из треугольника
.
Из треугольника![]() имеем:
имеем:![]() ,и так как
,и так как
![]()
![]()
![]() ,
то приходим к соотношению:
,
то приходим к соотношению:
![]() .
.
Перепишем полученное дифференциальное уравнение в виде:
Рис. 1
![]() ,
или
,
или![]() ,
откуда (если производные равны, то
функции отличаются на постоянную)
,
откуда (если производные равны, то
функции отличаются на постоянную)![]() ,
или
,
или![]() ,
следовательно,
,
следовательно,
![]()
Обозначая
![]() через
через![]() ,
получаем окончательно:
,
получаем окончательно:
![]() .
.
Условиям задачи удовлетворяет семейство, зависящее от одного параметра, равносторонних гипербол, для которых оси координат служат асимптотами.
Задача 2.Распад радия происходит таким образом, что скорость распада пропорциональна наличному количеству радия. Найти закон, выражающий изменение количества радия с течением времени, если известно, что через 1600 лет останется половина количества радия.
Решение. Пусть![]() – количество радия и
– количество радия и![]() – время (в годах). Найдем зависимость
– время (в годах). Найдем зависимость![]() от
от![]() :
:![]() .
Из условий задачи (скорость изменения
есть производная по времени):
.
Из условий задачи (скорость изменения
есть производная по времени):
![]() .
.
Перепишем полученное уравнение в виде
![]()
и из равенства дифференциалов
![]() заключаем, что сами функции отличаются
на постоянную:
заключаем, что сами функции отличаются
на постоянную:![]() (*).
(*).
Пусть в начальный момент
![]() количество радия
количество радия![]() .
Это дает возможность из (*) найти
соответствующее значение
.
Это дает возможность из (*) найти
соответствующее значение![]() :
:![]() .
Таким образом,
.
Таким образом,
![]() .
.
Коэффициент
![]() находим из условия, что при
находим из условия, что при![]()
![]() :
:
![]() ,
,
откуда
![]() .
Следовательно,
.
Следовательно,
![]() ,
,
или
![]() .
.
З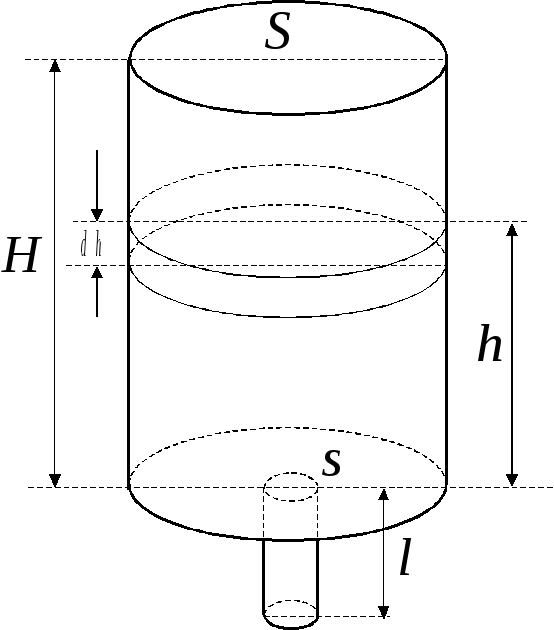 адача
3.Вода вытекает через отверстие в дне
цилиндрического сосуда. По какому закону
будет понижаться уровень воды в сосуде
с течением времени, если известно, что
скорость
адача
3.Вода вытекает через отверстие в дне
цилиндрического сосуда. По какому закону
будет понижаться уровень воды в сосуде
с течением времени, если известно, что
скорость
![]() истечения жидкости из отверстия зависит
от высоты
истечения жидкости из отверстия зависит
от высоты![]() столба жидкости следующим образом
столба жидкости следующим образом
![]() .
.
Решение.Обозначим (см. рис.2)
через![]() высоту сосуда.
высоту сосуда.
![]() ‑ площадь его основания,
s‑ площадь
отверстия и h
‑ высоту жидкости в сосуде в
момент времениt.
‑ площадь его основания,
s‑ площадь
отверстия и h
‑ высоту жидкости в сосуде в
момент времениt.
В течение промежутка времени от tдо
![]() высота уровня в сосуде понизится
c hдо
высота уровня в сосуде понизится
c hдо
![]() .
За это время из сосуда вытечет объем
воды, равный‑
.
За это время из сосуда вытечет объем
воды, равный‑
![]() .
Таков же должен быть объем струи жидкости,
вытекшей за это время из отверстия. Он
равен площади s,умноженной на длину пути
.
Таков же должен быть объем струи жидкости,
вытекшей за это время из отверстия. Он
равен площади s,умноженной на длину пути![]() ,пройденного частицей жидкости с момента
tдо
,пройденного частицей жидкости с момента
tдо
![]() .Движение ее неравномерно: в момент
.Движение ее неравномерно: в момент![]() скорость
скорость![]() ,
а в момент
,
а в момент
![]()
![]() .Для
.Для
Рис. 2. вычисления длины
пройденного пути воспользуемся средней
скоростью:
![]() ,
где
,
где
![]() .
.
Мы приходим, таким образом, к соотношению:
![]() .
.
Отсюда
![]() ,
,![]() .Переходя
к пределу при
.Переходя
к пределу при![]() ,
получаем дифференциальное уравнение
задачи:
,
получаем дифференциальное уравнение
задачи:
![]() .
.
Решаем его тем же способом, что и предшествующее уравнение:
![]() .
.
Замечая, что в момент
![]() ,
,
![]() ,находимС:
,находимС:![]() .И таким образом, приходим к равенству:
.И таким образом, приходим к равенству:![]() ,
откуда
,
откуда
![]() .
.
Таков закон истечения жидкости из
отверстия в дне сосуда. Полагая
![]() ,находим, что вся жидкость вытечет из
сосуда за
,находим, что вся жидкость вытечет из
сосуда за ![]() сек.
сек.
Задача 4.Найти такую кривую, проходящую
через точку![]() ,
чтобы тангенс угла наклона касательной
в любой ее точке равнялся ординате этой
точки, увеличенной на 3 единицы.
,
чтобы тангенс угла наклона касательной
в любой ее точке равнялся ординате этой
точки, увеличенной на 3 единицы.
Решение.Исходя из геометрического смысла первой производной, получаем дифференциальное уравнение семейства кривых, удовлетворяющих требуемому в задаче свойству, а именно
![]() или
или![]()
Откуда
![]() .
.
Так как искомая кривая должна проходить
через точку
![]() ,
т. е.
,
т. е.![]() ,
то значение
,
то значение
![]() ,соответствующее этой кривой определяем
из условия:
,соответствующее этой кривой определяем
из условия:![]() ,
т. е.
,
т. е.![]() ,
так что
,
так что![]() ,
откуда
,
откуда
![]() .
.
В силу условия
![]() должен быть выбран знак плюс:
должен быть выбран знак плюс:![]() .
.
Задача 5.В цилиндрическом сосуде
объемом![]() ,
заключен атмосферный воздух, который
адиабатически (без обмена тепла с
окружающей средой) сжимается до объема
,
заключен атмосферный воздух, который
адиабатически (без обмена тепла с
окружающей средой) сжимается до объема
![]() .
Вычислить работу сжатия.
.
Вычислить работу сжатия.
Решение.Известно, что адиабатический процесс характеризуется уравнением Пуассона
![]() ,
(1)
,
(1)
где ![]() –первоначальный объем газа,
–первоначальный объем газа,
![]() – первоначальное давление газа,
– первоначальное давление газа,
![]() – постоянная для данного газа величина.
– постоянная для данного газа величина.
Обозначим через
![]() и
и![]() соответственно объем и давление газа
в тот момент, когда поршень находится
на высоте
соответственно объем и давление газа
в тот момент, когда поршень находится
на высоте![]() ,
а через
,
а через
![]() – площадь поршня. Тогда при опускании
поршня на величину
– площадь поршня. Тогда при опускании
поршня на величину
![]() объем газа уменьшится на величину
объем газа уменьшится на величину
![]() .При этом будет выполнена работа
.При этом будет выполнена работа
![]() или
или ![]() .(2)
.(2)
Находя
![]() из уравнения Пуассона (1) и подставляя
в (2), получим дифференциальное уравнение
процесса:
из уравнения Пуассона (1) и подставляя
в (2), получим дифференциальное уравнение
процесса:
![]() .
(3)
.
(3)
Интегрируя (3), будем иметь:
![]() .
(4)
.
(4)
Согласно начальному условию
![]() из (4) получим
из (4) получим
![]() .
.
Таким образом, работа адиабатического
сжатия (от
![]() до
до![]() )будет
)будет
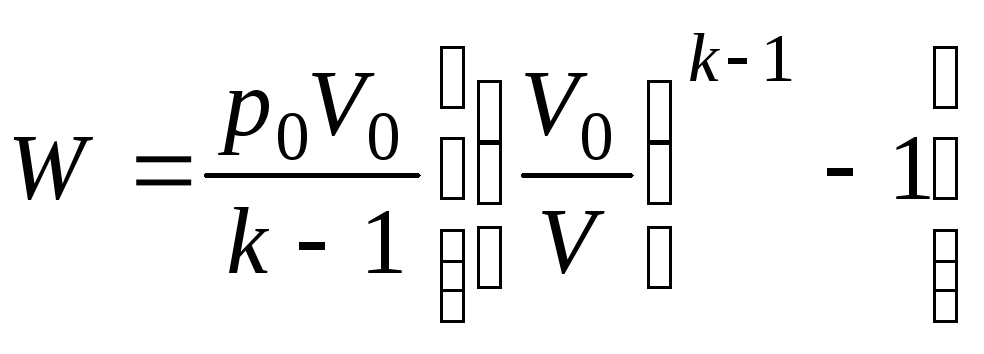 .
(5)
.
(5)
При
![]() получаем
получаем
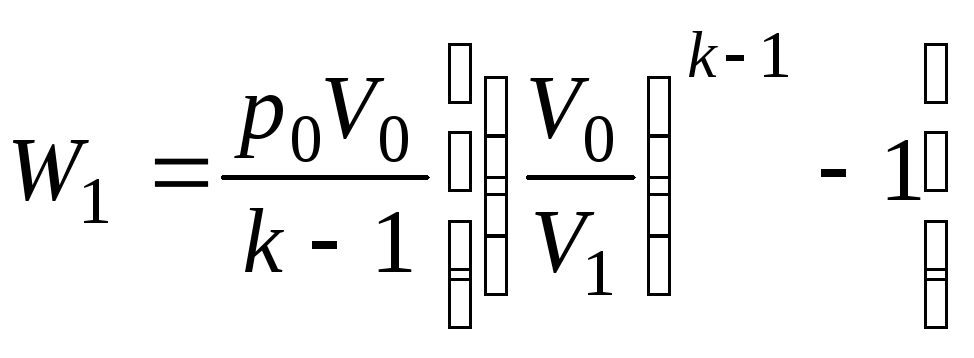 .
.
