3.11. Остовы графа. Построение минимального остова
Напомним, что подграф
 графа
графа ,
называется остовным подграфом, если
,
называется остовным подграфом, если .
.
Определение.Остовом
обыкновенного графа называется его
остовный подграф, являющийся деревом.
Пусть
 - обыкновенный граф. Упорядочим множество
его вершин
- обыкновенный граф. Упорядочим множество
его вершин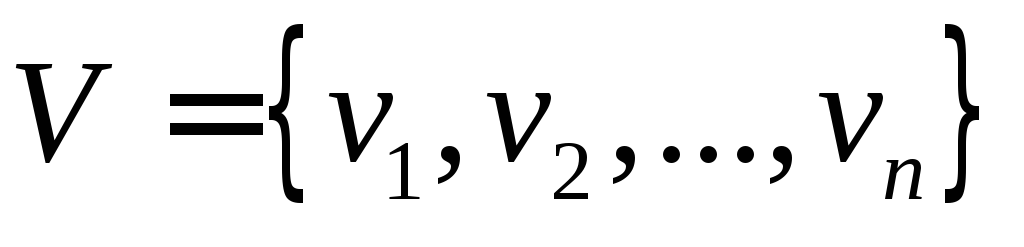 .
Определимматрицу Кирхгофа
.
Определимматрицу Кирхгофа
 графа
графа ,
полагая:
,
полагая:
 ,
,
где
 - матрица смежности графа, отвечающая
данному упорядочению вершин.
- матрица смежности графа, отвечающая
данному упорядочению вершин.
Можно показать, что матрицы Кирхгофа
обладают следующим свойством:
алгебраические дополнения всех
элементов любой из матриц Кирхгофа
графа равны между собой.
Утверждение.Число остовов в
связном неодноэлементном обыкновенном
графе равно алгебраическому дополнению
любого элемента его матрицы Кирхгофа.
Доказательство этого утверждения
опустим.
Определение.Взвешенным
графом будем называть совокупность
объектов
 ,
где тройка
,
где тройка
 - граф и
- граф и -
отображение, называемое весовым.
-
отображение, называемое весовым.
Число
 называетсявесомребра
называетсявесомребра ,
число
,
число -весомграфа
-весомграфа .
.
Определение.Остов
 связного взвешенного графа
связного взвешенного графа
 назовем минимальным
остовом, если для любого остова
назовем минимальным
остовом, если для любого остова
 выполнено неравенство
выполнено неравенство
 .
.
Рассмотрим задачу о нахождении
минимального остова в связном взвешенном
графе.
Теорема (алгоритм Краскала). Пусть
 - связный взвешенный граф.
- связный взвешенный граф.
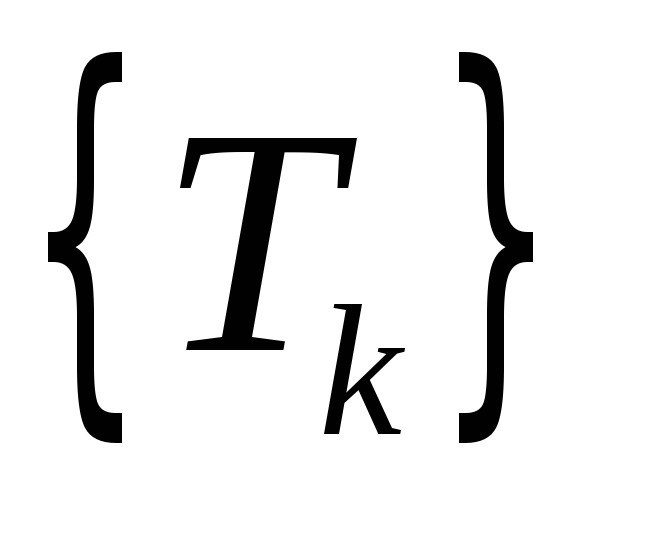 -
последовательность его остовных
подграфов, заданная индуктивно следующим
образом:
-
последовательность его остовных
подграфов, заданная индуктивно следующим
образом:
1.  остовный подграф, множество
остовный подграф, множество 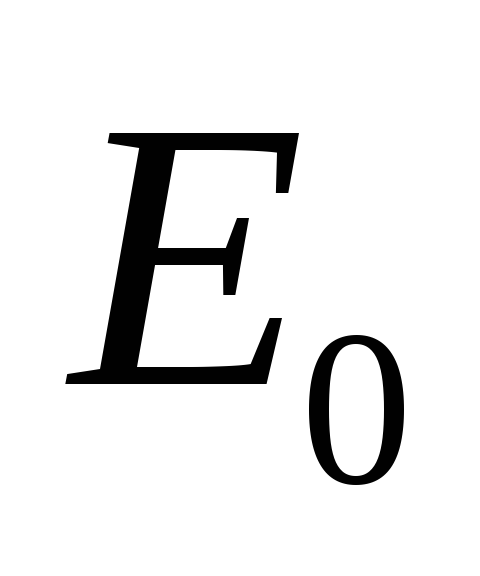 ребер которого пусто.
ребер которого пусто.
2. Пусть  - остовный подграф с множеством ребер
- остовный подграф с множеством ребер
 .Тогда
.Тогда  - остовный подграф с множеством ребер
- остовный подграф с множеством ребер
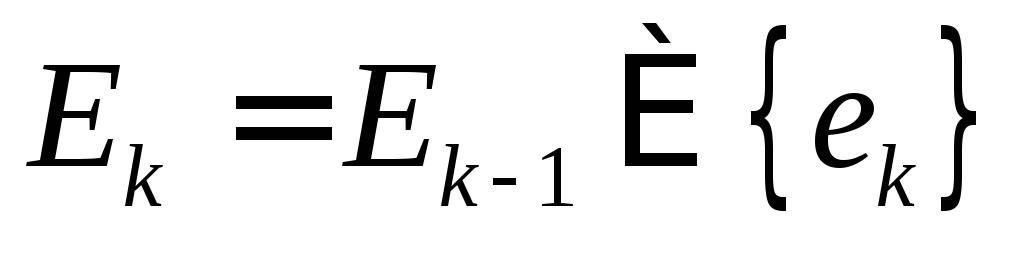 ,
где ребро
,
где ребро  выбирается из множества
выбирается из множества  так, что выполнены два условия: а)
добавление ребра
так, что выполнены два условия: а)
добавление ребра 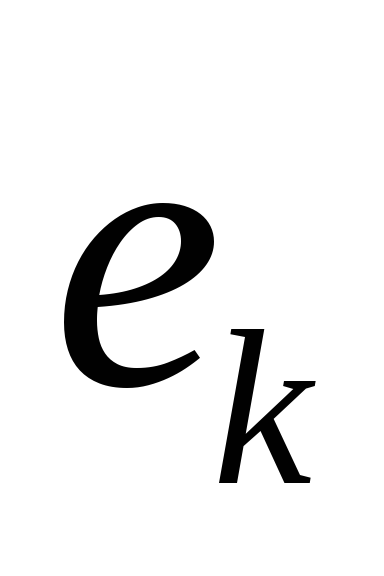 не приводит к образованию циклов; б) из
ребер, удовлетворяющих условию а), ребро
не приводит к образованию циклов; б) из
ребер, удовлетворяющих условию а), ребро
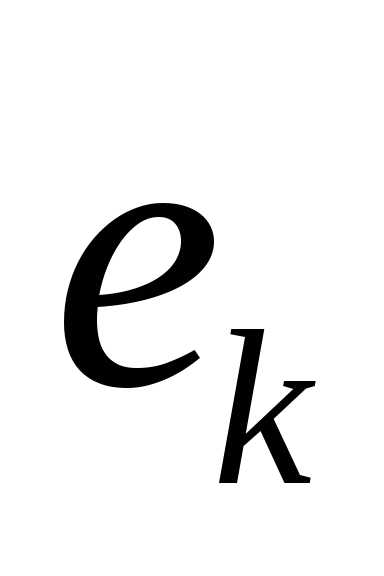 обладает наименьшим весом.
обладает наименьшим весом.
Тогда последним элементом
последовательности  является минимальный остов графа
является минимальный остов графа  .
.
Доказательство теоремы опустим.
Замечания.1. Если граф несвязен,
то по алгоритму Краскала строится
остовный лес.
2. Если граф невзвешен, то, присваивая
всем ребрам одинаковые веса, мы можем
применить алгоритм Краскала для
построения остова (остовного леса).
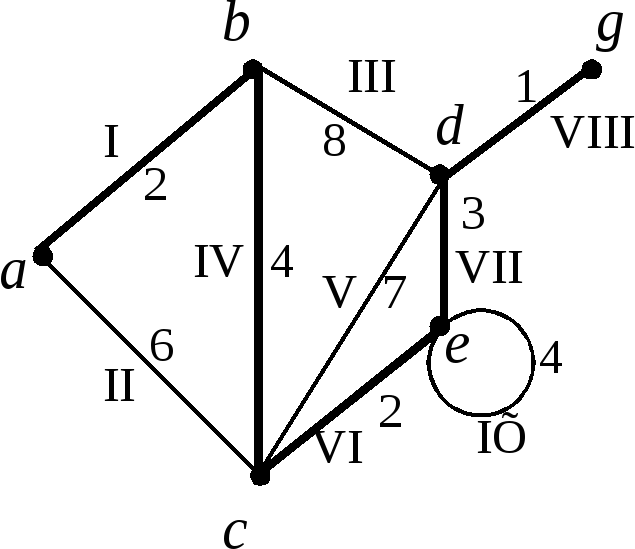
Пример 1.Построить остов минимального веса графа с множеством вершин
с множеством вершин  ;
множеством ребер
;
множеством ребер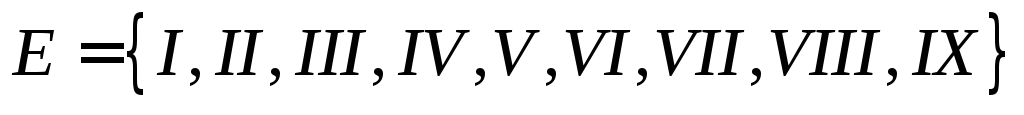 ;
отображением инцидентности
;
отображением инцидентности ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, и весовым отображением
и весовым отображением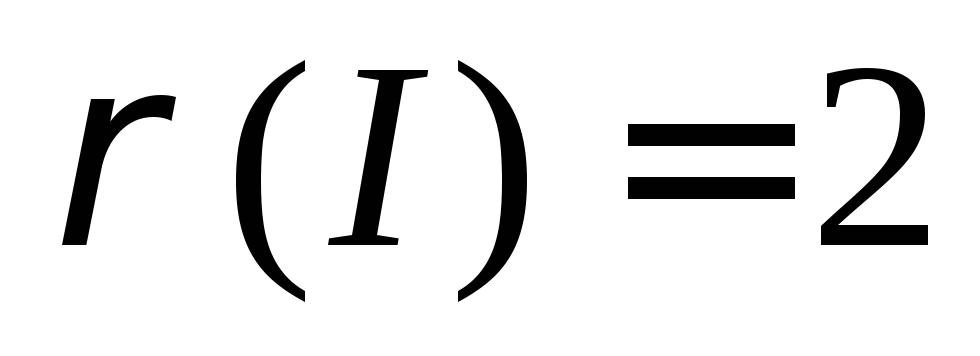 ,
,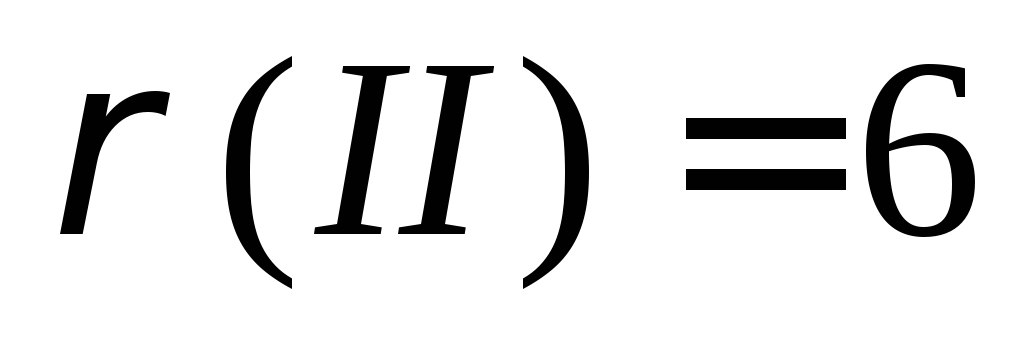 ,
,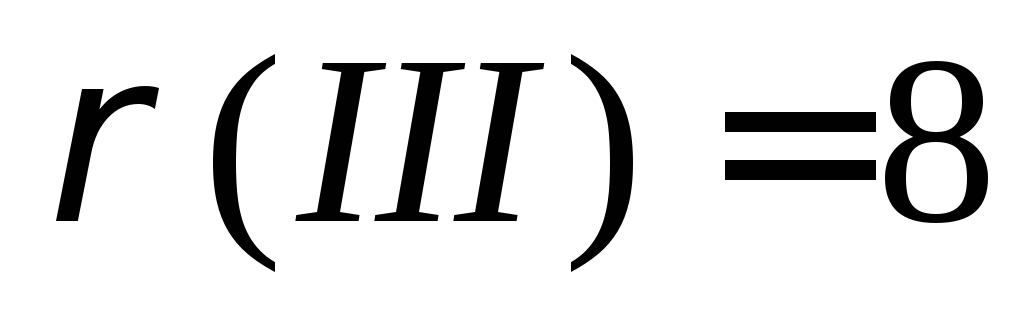 ,
, ,
, ,
, ,
, ,
, .
.
Согласно алгоритму Краскала строим
последовательность остовных подграфов:
 с пустым множеством ребер;
с пустым множеством ребер;
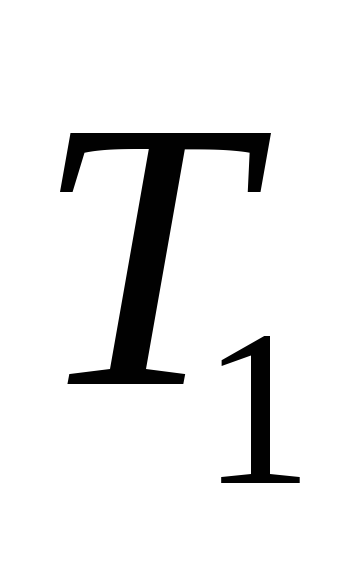 с множеством ребер
с множеством ребер ;
;
 с множеством ребер
с множеством ребер ;
;

 с множеством ребер
с множеством ребер ;
;
 с множеством ребер
с множеством ребер ;
;
 с множеством ребер
с множеством ребер .
.
Добавление к графу
 любого из оставшихся ребер графа
любого из оставшихся ребер графа ведет к образованию цикла. Таким образом,
подграф
ведет к образованию цикла. Таким образом,
подграф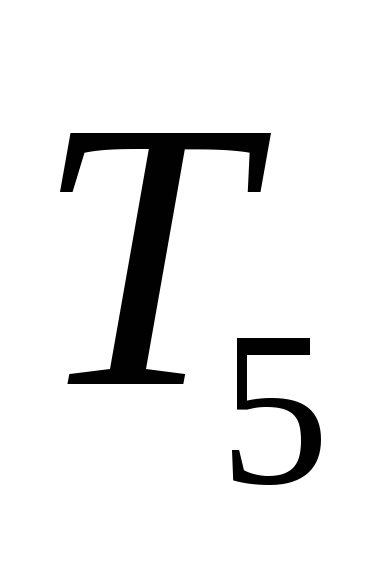 cмножеством ребер
cмножеством ребер ,
- минимальный остов, вес которого равен
,
- минимальный остов, вес которого равен .
.
49


 ,
, с множеством ребер
с множеством ребер