
3.10. Кодирование деревьев
Выделим в дереве какую-нибудь одну вершину, которую назовем корнем. Полученное дерево с выделенной вершиной называетсякорневым.
Для задания (с точностью до изоморфизма) корневыхдеревьев используюткод из 0 и 1, который мы определим индуктивно.
О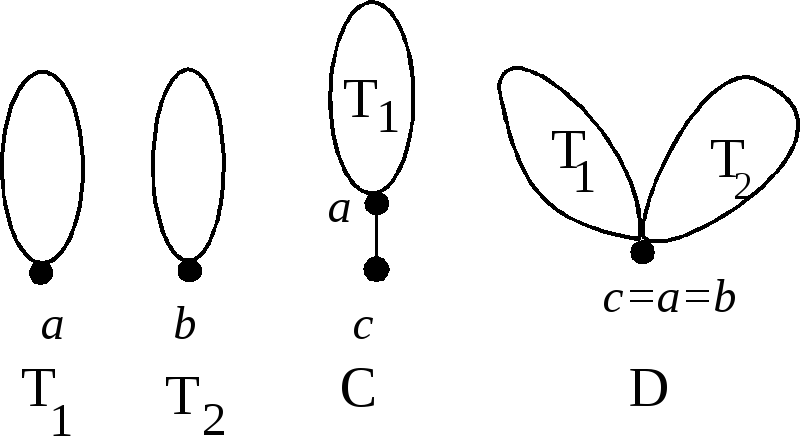 пределение.Кодом корневого дерева с одним ребром
является
пределение.Кодом корневого дерева с одним ребром
является ![]() .Пусть деревья
.Пусть деревья ![]() и
и
![]() с корнямиa и b
соответственно (см. рис.) имеют коды
с корнямиa и b
соответственно (см. рис.) имеют коды ![]() и
и ![]() .Тогда кодом дерева
.Тогда кодом дерева ![]() с корнем с является код
с корнем с является код ![]() ,
а кодом дерева
,
а кодом дерева ![]() с корнем
с корнем ![]() - код
- код![]() .
.
Пример 1. Написать код дерева, изображенного на рисунке.
И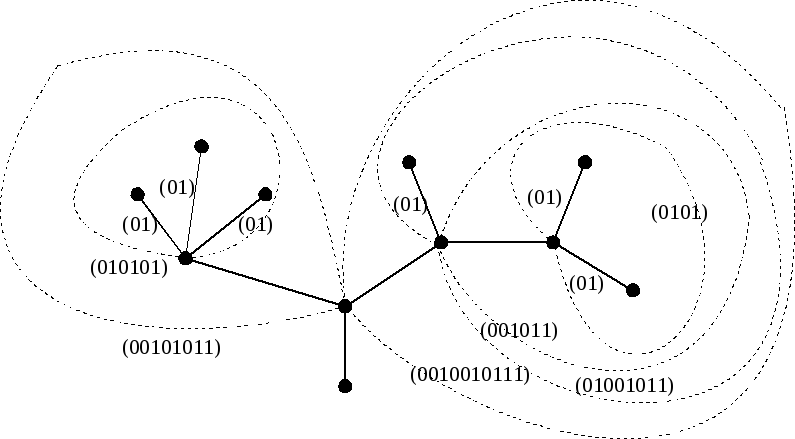 так,
код дерева -
так,
код дерева -![]() .
.
Справедливо следующее утверждение:для того, чтобы последовательность нулей и единиц являлась кодом некоторого дерева необходимо и достаточно, чтобы число нулей и единиц в этой последовательности было одинаковым, причем в любом начальном отрезке последовательности количество нулей было не меньше количества единиц.
Чтобы построить корневое дерево по кодуиз нулей и единиц, нужно разбить последовательность на пары 0 и 1, следуя правилу: первая попавшаяся в коде единица образует пару с предшествующим нулем; каждая следующая единица образует пару с ближайшим слева неиспользованным нулем. Если образованные таким образом пары пометить снизу кода фигурными скобками, то каждая такая скобка будет соответствовать ребру графа.
П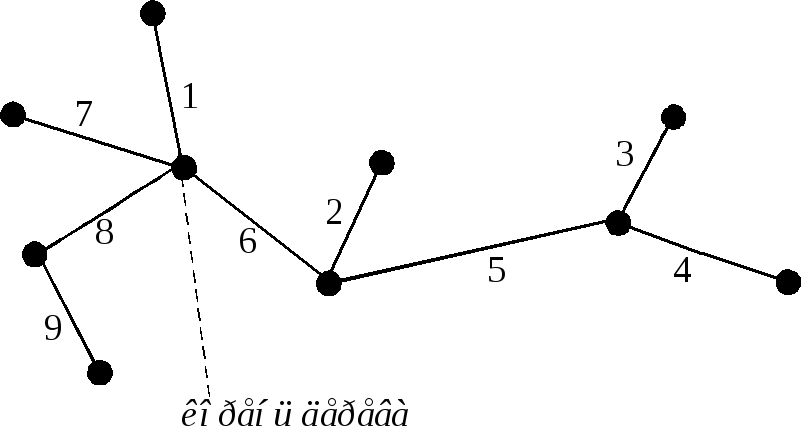 ример
2.Построить дерево по коду
ример
2.Построить дерево по коду .
.
Для задания помеченныхдеревьев, т.е. деревьев, вершины которых занумерованы, используют код из натуральных чисел.
Пусть дано помеченное дерево. Чтобы построить его код из натуральных чисел действуем следующим образом. Находим висячую вершину с наименьшим номером. Записываем номер смежной с ней вершины (это начало кода), после чего удаляем эту висячую вершину вместе с инцидентным ей ребром. Для полученного в результате данной операции дерева находим висячую вершину с наименьшим номером, записываем номер смежной с ней вершины (это продолжение кода), после чего удаляем эту висячую вершину вместе с инцидентным ей ребром. Так поступаем до тех пор, пока не останется последнее ребро.
Заметим, что длина кода из натуральных чисел на единицу меньше числа ребер и на две единицы меньше числа вершин данного дерева.
П ример
3.На рисунке изображено помеченное
дерево. Его код
ример
3.На рисунке изображено помеченное
дерево. Его код![]() .
.
Построение дерева по коду из натуральных
чиселрассмотрим на примере кода![]() .
Прежде всего, заметим, что дерево, которое
нам предстоит построить, имеет 8 вершин.
.
Прежде всего, заметим, что дерево, которое
нам предстоит построить, имеет 8 вершин.
|
2 |
2 |
4 |
4 |
6 |
6 |
|
1 |
2 |
4 |
4 |
6 |
6 |
|
1 |
3 |
4 |
4 |
6 |
6 |
|
1 |
3 |
2 |
4 |
6 |
6 |
|
1 |
3 |
2 |
5 |
6 |
6 |
|
1 |
3 |
2 |
5 |
4 |
6 |
|
1 |
3 |
2 |
5 |
4 |
7 |
|
2 |
2 |
4 |
4 |
6 |
6 |
