
3.9. Деревья и леса
Определение.Граф без циклов, называется ациклическим графом или лесом.
Определение.Связный ациклический граф называется деревом.
Каждая компонента связности леса –
дерево, следовательно, для
![]() -связного
леса существует дизъюнктное разбиение
на
-связного
леса существует дизъюнктное разбиение
на
![]() деревьев.
деревьев.
П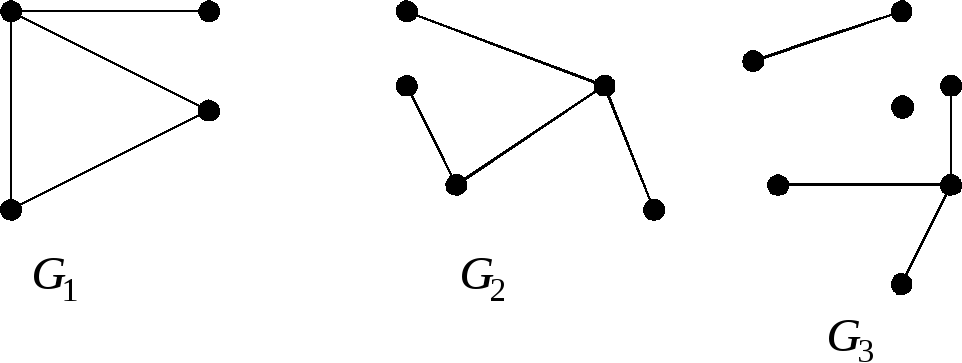 ример
1. Граф
ример
1. Граф
![]() не является деревом, не является лесом.
Граф
не является деревом, не является лесом.
Граф
![]() - дерево. Граф
- дерево. Граф
![]() - лес.
- лес.
Лемма. Если граф – дерево, то каждое его ребро является мостом.
Доказательство.В параграфе 3.6 было доказано, что если ребро графа не содержится ни в одном цикле, то оно является мостом. Дерево граф ациклический, следовательно, каждое его ребро мост.■
Теорема (основная теорема о деревьях).
Для графа
![]() следующие утверждения равносильны:
следующие утверждения равносильны:
Граф
 - дерево.
- дерево. ациклический
и
ациклический
и 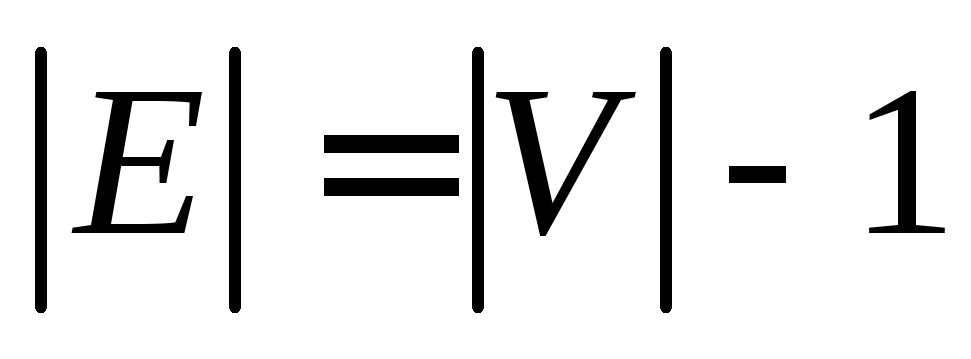 .
. связный и
связный и  .
. связный и каждое его ребро является
мостом.
связный и каждое его ребро является
мостом. Любые две вершины графа
 можно соединить, притом единственной,
простой цепью.
можно соединить, притом единственной,
простой цепью. ациклический,
и добавление к нему нового ребра приводит
к образованию единственного простого
цикла.
ациклический,
и добавление к нему нового ребра приводит
к образованию единственного простого
цикла.
Доказательство.Доказательство
проведем по следующей схеме:![]() .
.
![]() .
Индукцией по числу ребер проверим, что
для любого дерева выполняется равенство
.
Индукцией по числу ребер проверим, что
для любого дерева выполняется равенство![]() .
.
Базис индукции.Пусть![]() ,
тогда
,
тогда![]() ,
и равенство
,
и равенство![]() выполнено.
выполнено.
Индуктивный переход.Предположим, что требуемое равенство
выполняется для любого дерева с числом
ребер меньшим либо равным![]() .
Докажем, что оно справедливо и для дерева
с числом ребер
.
Докажем, что оно справедливо и для дерева
с числом ребер![]() .
Удалим из графа
.
Удалим из графа![]() произвольное ребро
произвольное ребро
![]() .Согласно лемме, ребро
.Согласно лемме, ребро
![]() - мост. По теореме о мостах
- мост. По теореме о мостах![]() .
Следовательно, граф
.
Следовательно, граф![]() состоит из двух компонент связности,
состоит из двух компонент связности,![]() и
и ![]() ,
каждая из которых – дерево с числом
ребер меньшим либо равным
,
каждая из которых – дерево с числом
ребер меньшим либо равным![]() .
Для каждой компоненты связности
справедливо предположение индукции,
т.е. выполнены равенства
.
Для каждой компоненты связности
справедливо предположение индукции,
т.е. выполнены равенства![]() и
и![]() .
Складывая эти равенства почленно,
получим:
.
Складывая эти равенства почленно,
получим:![]() .
Или
.
Или![]() .
.
![]() .
Докажем, что если граф
.
Докажем, что если граф
![]() ациклический и
ациклический и![]() ,
то граф связный. Будем рассуждать от
противного, т.е. предположим, что найдется
ациклический граф
,
то граф связный. Будем рассуждать от
противного, т.е. предположим, что найдется
ациклический граф![]() ,
число ребер которого на единицу меньше
числа вершин, который связным не является.
Пусть
,
число ребер которого на единицу меньше
числа вершин, который связным не является.
Пусть![]() ,
,![]() ,
- число компонент связности графа
,
- число компонент связности графа![]() .
Каждая компонента связности - дерево.
Переход
.
Каждая компонента связности - дерево.
Переход![]() уже доказан, следовательно, для каждой
компоненты связности
уже доказан, следовательно, для каждой
компоненты связности![]() можем записать:
можем записать:![]() .
Просуммировав по
.
Просуммировав по![]() ,
получим:
,
получим:
![]() .
.
Или
![]() .
.
Так как
![]() ,
то пришли к противоречию с условием
,
то пришли к противоречию с условием![]() .
Следовательно, наше предположение было
неверным.
.
Следовательно, наше предположение было
неверным.
![]() .
Докажем, что если граф связный и
.
Докажем, что если граф связный и![]() ,
то каждое его ребро является мостом.
Будем рассуждать от противного.
Предположим, что найдется связный граф
,
то каждое его ребро является мостом.
Будем рассуждать от противного.
Предположим, что найдется связный граф![]() ,
такой что
,
такой что![]() ,
в котором есть ребро
,
в котором есть ребро
![]() ,
не являющееся мостом. Тогда граф
,
не являющееся мостом. Тогда граф![]() связный и
связный и
![]() .
.
То есть для связного графа
![]() выполняется условие
выполняется условие![]() ,
что противоречит следствию теоремы о
знаке цикломатического числа (см.
параграф 3.7).
,
что противоречит следствию теоремы о
знаке цикломатического числа (см.
параграф 3.7).
![]() .
Из связности графа вытекает, что любые
две его вершины можно соединить маршрутом,
и, следовательно, простой цепью. Докажем,
что эта простая цепь единственна.
Доказательство проведем от противного.
Предположим, что найдется связный граф,
все ребра которого - мосты, такой, что в
нем есть две вершины
.
Из связности графа вытекает, что любые
две его вершины можно соединить маршрутом,
и, следовательно, простой цепью. Докажем,
что эта простая цепь единственна.
Доказательство проведем от противного.
Предположим, что найдется связный граф,
все ребра которого - мосты, такой, что в
нем есть две вершины![]() и
и
![]() ,
соединенные двумя различными простыми
цепями
,
соединенные двумя различными простыми
цепями![]() и
и![]() .
Поскольку цепи
.
Поскольку цепи![]() и
и![]() различны, то имеется ребро
различны, то имеется ребро
![]() ,
входящее в цепь
,
входящее в цепь![]() и не входящее в цепь
и не входящее в цепь![]() .
.
Пусть
![]() и
и![]() - фрагменты цепи
- фрагменты цепи![]() .
Склеим инвертированный фрагмент
.
Склеим инвертированный фрагмент![]() ,
цепь
,
цепь![]() и инвертированный фрагмент
и инвертированный фрагмент![]() .
Получим на графе
.
Получим на графе![]()
![]() -
маршрут, не содержащий ребра
-
маршрут, не содержащий ребра
![]() .
Из этого маршрута выделим
.
Из этого маршрута выделим![]() -простую
цепь и склеим ее с цепью
-простую
цепь и склеим ее с цепью
![]() .
В результате получим цикл, содержащий
.
В результате получим цикл, содержащий
![]() ,
а это противоречит тому, что ребро
,
а это противоречит тому, что ребро
![]() - мост.
- мост.
![]() .
Пусть для графа
.
Пусть для графа![]() выполнено условие 5.
выполнено условие 5.
Проверим сначала, что граф
![]() не содержит циклов. Будем рассуждать
от противного. Предположим, что на графе
не содержит циклов. Будем рассуждать
от противного. Предположим, что на графе![]() имеется цикл. Пусть
имеется цикл. Пусть
![]() - одно из ребер этого цикла и вершины
- одно из ребер этого цикла и вершины![]() и
и
![]() - концы этого ребра. Тогда
- концы этого ребра. Тогда![]() - простая цепь, соединяющая вершины
- простая цепь, соединяющая вершины![]() и
и
![]() .
Обозначим ее
.
Обозначим ее![]() .
Удалим из графа
.
Удалим из графа![]() ребро
ребро
![]() .
Поскольку ребра циклов не являются
мостами и граф
.
Поскольку ребра циклов не являются
мостами и граф![]() связный, то граф
связный, то граф![]() также будет связным. Следовательно, на
графе
также будет связным. Следовательно, на
графе![]() существует
существует![]() -
маршрут. Выделим из этого маршрута
-
маршрут. Выделим из этого маршрута![]() -простую
цепь и обозначим ее
-простую
цепь и обозначим ее![]() .
Таким образом мы показали, что на графе
.
Таким образом мы показали, что на графе![]() есть две простые цепи, соединяющие
вершины
есть две простые цепи, соединяющие
вершины![]() и
и
![]() :
:![]() и
и![]() ,
что противоречит условию 5.
,
что противоречит условию 5.
Покажем, что добавление к графу
![]() нового ребра приводит к образованию,
притом единственного, цикла. Возьмем
на графе
нового ребра приводит к образованию,
притом единственного, цикла. Возьмем
на графе![]() две произвольные вершины
две произвольные вершины![]() и
и ![]() и соединим их новым ребром
и соединим их новым ребром![]() ;
получим граф
;
получим граф![]() .
По условию на графе
.
По условию на графе ![]() имеется единственная простая
имеется единственная простая![]() -цепь.
Склеив ее с цепью
-цепь.
Склеив ее с цепью![]() ,
получим на графе
,
получим на графе![]() простой цикл. Докажем, что этот цикл
единственный. Предположим, что при
добавлении ребра
простой цикл. Докажем, что этот цикл
единственный. Предположим, что при
добавлении ребра![]() образовалось два простых цикла. Тогда,
удалив из каждого из них ребро
образовалось два простых цикла. Тогда,
удалив из каждого из них ребро![]() ,
получим на графе
,
получим на графе![]() две простые
две простые![]() -цепи,
а наличие двух
-цепи,
а наличие двух![]() -цепей
противоречит условию.
-цепей
противоречит условию.
![]() .
Будем рассуждать от противного, т.е.
предположим, что существует несвязный
граф
.
Будем рассуждать от противного, т.е.
предположим, что существует несвязный
граф![]() ,
для которого выполнено условие 6. Возьмем
на этом графе две вершины, лежащие в
разных компонентах связности, и соединим
их ребром
,
для которого выполнено условие 6. Возьмем
на этом графе две вершины, лежащие в
разных компонентах связности, и соединим
их ребром![]() .
В результате образуется граф
.
В результате образуется граф![]() ,
для которого ребро
,
для которого ребро![]() является мостом и, следовательно, не
содержится ни в одном цикле. Таким
образом, добавление ребра
является мостом и, следовательно, не
содержится ни в одном цикле. Таким
образом, добавление ребра![]() не привело к образованию цикла, что
противоречит условию 6.■
не привело к образованию цикла, что
противоречит условию 6.■
Следствие 1. Неодноэлементное дерево имеет не менее двух висячих вершин.
Доказательство.Рассмотрим
произвольное дерево, имеющее не менее
двух вершин. Представим множество его
вершин![]() в виде
в виде![]() ,
где
,
где![]() - множество висячих вершин этого дерева.
Тогда
- множество висячих вершин этого дерева.
Тогда
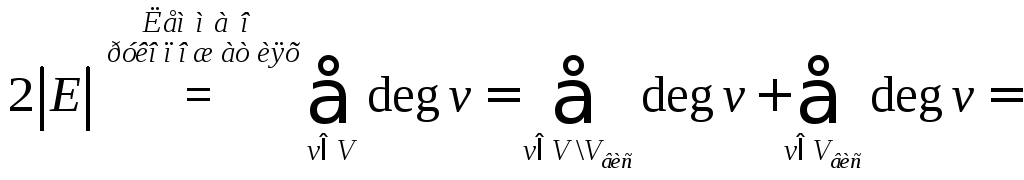
![]()
![]() .
.
Но
![]() ,
поэтому
,
поэтому
![]() .
.
Откуда
![]() . ■
. ■
Следствие 2. Если граф
![]() -
-
![]() -связный
лес, то
-связный
лес, то![]() .
.
Последнее следствие рекомендуем доказать самостоятельно.
